复杂背景下基于AD-GAC模型和最大熵阈值法的叶片病斑分割

赵辉 芮修业 岳有军 王红君

摘要：旨在研究复杂背景下叶片病斑的分割。由于复杂背景会带来巨大的噪声，产生过多的边缘和灰度值不均匀的区域，很容易导致过分割的现象，因此在复杂背景下，很难通过1次分割就完成对叶片病斑的分割。为了解决复杂背景下过分割的现象，提出两步分割的策略。第1步先用笔者提出的各向异性扩散测地线活动轮廓模型（anisotropic diffusion geodesic active contour model，简称AD-GAC模型）进行预分割，在此过程中构造新的边缘检测函数（edge stop function，简称ESF）;第2步通过最大熵阈值法完成最终的分割。随后，提取并计算预分割部分各像素灰度值的最大熵，以得到病斑部分与叶片部分的灰度值阈值，通过阈值来完成最后1步的分割。通过MATLAB仿真，可以证明该算法可以有效地将病斑从复杂背景下的叶片上分割出来。研究结果后续的病斑识别作了铺垫。

关键词：各向异性扩散;测地线活动轮廓;复杂背景;最大熵阈值法;病斑分割

中图分类号： S126文献标志码： A

文章编号：1002-1302（2019）18-0136-05

收稿日期：2018-06-14

基金项目：天津市科技计划（编号：15ZXZNGX00290）;天津市农业科技成果转化与推广项目（编号：201203060、201303080）。

作者简介：赵 辉（1963—），男，天津人，博士，主要研究方向为复杂系统智能控制理论与应用、农业信息与精准农业智能监测理论与技术。E-mail：zhaohui3379@126.com。

通信作者：芮修业，硕士研究生，主要研究方向为数字图像处理与模式识别。E-mail：292318849@qq.com。

我国是一个农业大国。在设施农业中，如果我们能准确地确定作物疾病的时间线，并及时作出处理，可以极大地提高国家农业的经济收益。对于经济作物的病害诊断而言，一个巨大挑战就是作物复杂的自然生长环境带来的影响[1]。图像分割技术对于后期关于病斑特征的提取和识别任务是至关重要的，并且分割效果的好坏将直接影响病斑的识别效果[2]。

图像分割技术目前已经在很多方面被提出，但是面对各种复杂的分割条件，还没有一种方法是普遍适用的，尤其是对于复杂背景下的叶片病斑分割[3]。大多数主流分割算法，无论是基于区域的分割算法[4]还是基于边缘的分割算法[5]，对于复杂背景下的叶片病斑分割效果都不尽如人意。

作为策略的第一步，笔者选择活动轮廓模型进行预分割。活动轮廓模型已经被证明可以成功地运用于核磁共振成像（MRI）图像的病斑分割[6]。然而，这种方法尚不能被成熟地运用于复杂背景下的植物叶片病斑分割。活动轮廓的研究开始于Snake模型的提出[7]。此模型通过在图像中的最小化能量函数来完成对图像中目标的分割，最小化能量函数的方法是水平集方法（level set method，简称LSM）。在这个过程中，我们可以得到模型演化的偏微分方程。其中1种LSM是基于边缘信息的[8]，GAC（测地线活动轮廓）模型[9]就是其中1个基于边缘信息的模型。GAC模型最终可以得到1个闭合轮廓，这是1个可以利用的特征。GAC模型利用图像的梯度信息去构造能量函数，开始设置的初始轮廓随着演化可以收敛在目标物体的边缘。但是GAC模型对噪声很敏感，复杂背景下的高噪声会影响曲线的演化，使得活动轮廓不能靠近叶片和病斑的边缘。如果不能成功地获得1个合适的预分割结果，那也不能得到合适的灰度值阈值，这也会导致最终的分割失败。

为了克服GAC模型在复杂背景下不能完成对叶片病斑预分割的局限性。本研究提出的各向异性扩散测地线活动轮廓模型（anisotropic diffusion geodesic active contour model，简称AD-GAC模型）比传统GAC模型的边缘检测函数（edge stop function，简称ESF）增加了各向异性扩散滤波器。各向异性扩散滤波器能够在去除噪声的同时增强边缘信息[10]，本研究将原来的外部能量函数转变成了可以自动去除噪声、增强图像梯度信息的新的外部能量函数。因此，用于AD-GAC模型内部运算的是强化过的梯度信息，各向异性扩散作为外部能量函数的一部分，是一种技术的融合而不仅仅是简单的堆积。此外，笔者用惩罚项作为内部能量函数，可以避免重新初始化带来的时间上的巨大消耗。最后，通过将预分割部分像素的灰度值放入与原图维度相同的全零矩阵来提取预分割结果，然后，将提取部分的像素灰度值作为第2部分的输入数据，通过计算最大熵得到阈值，完成最终的病斑分割。

1 相关工作基础

1.1 各向异性扩散

在图像处理和计算机领域，各项异型扩散的核心是Perona-Malik方程，所以各向異性扩散模型也称为P-M模型。这是一种在保留图像重要部分的同时消除图像噪声的技术。特别是对于图像中的边缘、线条或其他重要部分。从原理上看，各向异性扩散是在考虑目标边界之后平均边界一侧的像素值。各向异性扩散可以表示为如下公式[10]：

It=div[c（‖I‖）·I]I（t=0）=I0。（1）

式中：c（‖I‖）是扩散因子。

P-M模型的扩散方程可以表示为如下公式：

c（‖I‖）=exp[-（‖I‖/k）2]。（2）

式中：k是扩散门限，根据本试验情况，将k值设为15。本研究将利用各向异性扩散后的图像梯度信息来构造新的ESF。

1.2 水平集方法

LSM的基本思想是将n维曲面演化为在（n+1）维空间中求水平集曲面的隐函数解。用1条平面闭合曲线隐含地表示水平集函数的零水平集：

C（t）={（x，y）|（x，y，t）=0}。（3）

水平集演化方程[11]如下：

t=F||（x，y，0）=0（x，y）。（4）

式中：F控制著水平集函数演化的速度;为梯度算子。

2 AD-GAC模型

在复杂背景下，传统GAC模型的ESF在边缘检测方面存在对噪声敏感的缺点。复杂背景下的一些阴影、水珠、交错的遮挡的叶片都会产生很多无法定义的边缘。由于梯度信息的变化，轮廓将不会收敛在预期的目标边缘。

AD-GAC的核心在于各向异性扩散滤波器，各向异性扩散滤波器的离散表达式可以写成如下形式：

It+1p=Itp+λ1|ηp|∑q∈ηpc（Itp，q）Itp，q。（5）

式中：控制系数λ1是1个控制着总体扩散强度的常量，经过多次试验，在本研究中将其设置为0.2;|ηp|表示邻域空间的大小，一般选择4-型邻域空间。以Ip作为边缘检测因子的一部分：

Is=Ip×Gσ。（6）

式中：Ip表示各向异性扩散后的图像强度;Is表示对Ip进行高斯滤波后的结果;Gσ是带有标准差的高斯核函数。x轴、y轴方向上的梯度可以按如下公式进行计算：

Ix，Iy=Ist。（7）

因此，新的ESF可以被定义为下式：

gd=11+f， f=I2x+I2y。（8）

利用gd，1个新的外部能量函数就可以自然地被定义为如下形式：

ζgd，λ，v（）=λ2∫Ωgd·δ（）||dxdy+v∫Ωgd·H（-）dxdy。（9）

式中：δ是单变量狄拉克函数;H是海氏函数;λ2是加权长度项的系数;v是加权区域项的系数，如果初始轮廓在目标的外面，v选择正值，反之，v选择负值。

经过很多轮迭代之后，水平集函数会失去平滑性和距离特性[12]，为了避免这个系统缺陷，本研究利用惩罚项作为内部能量函数[13]。用于最小化能量函数的最陡梯度下降流公式定义为如下形式：

t=μ[Δ-div||]+vgdδ（）+λ2δ（）divgd||。（10）

式中：μΔ-div||是惩罚项，也就是整个能量函数的内部能量函数，其中，μ是惩罚项系数，当时间步长T满足T·μ<0.25时，水平集函数的演化可以保持稳定，时间步长T可以根据具体情况进行选择。

经过大量对比试验，笔者发现，当T=5，μ=0.04，迭代次数为1 000次时，AD-GAC模型的能量函数收敛效果最好。

3 分割的第2步

在分割的第2步，笔者将完成对于复杂背景下叶片病斑分割的最后一部分，利用预分割结果，本研究可以获得叶片和病斑的灰度值阈值，从而区分叶片部分和病斑部分。

3.1 移除背景

为了移除背景，笔者首先构造1个与原图维度相同的全零矩阵，同时，获得预分割结果部分的每个像素的坐标。根据坐标，将对应的各向异性扩散后的图像的像素灰度值按照坐标对应地放进全零矩阵中。

整个移除背景的过程如下所示：

（1）假设各向异性扩散后的图像（维度与原图相同）是1个维度为5×5的矩阵，假设预分割结果如图1所示。

（2）假设预分割部分像素的坐标为（1，2），（1，3），（2，2），（2，3），（2，4），（3，2），（3，3），（3，4），（4，2），（4，3），（4，4），（5，2）。

（3）构造1个维度为5×5的全零矩阵（图2）。

（4）将上述坐标对应各向异性扩散的像素灰度值放进全零矩阵中（图3）。

算法描述——移除背景：

u：预分割结果的二值图像

U：原图像的单通道图

p：各向异性扩散结果

步骤：

（1） 找到预分割区域所有像素的坐标：

[row，col，v]=find（u>0）

（2） 将坐标存在a1中：

a1=[row，col]

（3） 构造1个与原图维度相同的全零矩阵b1：

[x，y]=size（U）

b1=zeros（x，y）

（4） 将p中对应坐标的灰度值放进b1中：

[t，t1]=size（a1）

for q=1 to t do

m1=a1（q，1）

n1=a1（q，1）

b1（m1，n1）=p（m1，n1）

end for

3.2 最大熵阈值

在去除背景后，只剩下主要病斑和一些带有病斑的叶片。所以现在矩阵b1中含有3种类型的元素：（1）零元素（背景区域）;（2）叶片部分的灰度值;（3）病斑部分的灰度值。

将矩阵b1中的数据转化为一维数据，去除零元素，作为最大熵阈值法[14]的输入。

在去除背景后的图中，含有2种不同的灰度值区域，那必然存在1个灰度值t，作为阈值，可以得到最佳分割结果。假设叶片区域的灰度值范围是a～t，该区域的概率分布为∑ti=ah（i），病斑区域的灰度值范围是（t+1）～b，该区域的概率分布为∑bi=t+1h（i）。概率分布应该满足：

∑tah（i）+∑bt+1h（i）=1。（11）

叶片区域像素灰度值的熵为

Hlesion（t）=-∑ti=ah（i）∑tj=ah（j）log2h（i）∑tj=ah（j）。（12）

病斑区域像素灰度值的熵为

Hleaf（t）=-∑bi=t+1h（i）∑bj=t+1h（j）log2h（i）∑bj=t+1h（j）。（13）

根据信息论，当阈值能够最佳区分2个区域的时候，熵应该最大，所以最佳阈值可以通过最大化2种类型像素的熵来选择：

T=ArgMaxt=a，…，bHlesion（t）+Hleaf（t）。（14）

根据最佳阈值，将b1矩阵中灰度值小于T的值设置为0，剩下的就是病斑区域。至此，本研究就完成了复杂背景下对于叶片病斑的分割。

4 结果与分析

为了评估笔者提出的算法框架的效果，本研究选择几幅复杂背景下的叶片病斑图进行测试，数据图片来自本研究所在的试验农场，图片的像素值分别为395×395和640×427。

根据本试验内容，参数的具体选择如下：各向异性扩散光滑系数λ1=0.1，时间步长T=5，惩罚项系数μ=0.04，加权长度项系数λ2=5，加权区域项系数v=3，AD-GAC模型迭代次数为1 000次。程序运行的硬件环境如下：Windows7旗舰版（32-bit），内核为i5-4590 3.30-GHz处理器，运行内存为4 GB。

图4展示了AD-GAC模型相对于GAC模型在复杂背景下对于叶片病斑预分割的优越性，可以看出，由于原图的复杂背景带来过多的边缘信息，导致GAC模型无法很好地收敛

到病斑以及带有病斑的叶片周圍，过多的预分割区域意味着进入下一步分割的像素灰度值有更大的范围，会直接影响最大熵阈值法求得的最佳阈值的准确度。

完整的分割过程如图5所示。从图5-b可以看出，利用gd构建的外部能量函数能使水平集轮廓较为准确地收敛在病斑以及带有病斑的叶片周围。如图5-c所示，为了避免复杂背景带来的干扰，将预分割结果从复杂背景中提取出来。从图5-d可以看出，最终的分割结果有效避免了过分割现象，并且能够得到准确的病斑区域。

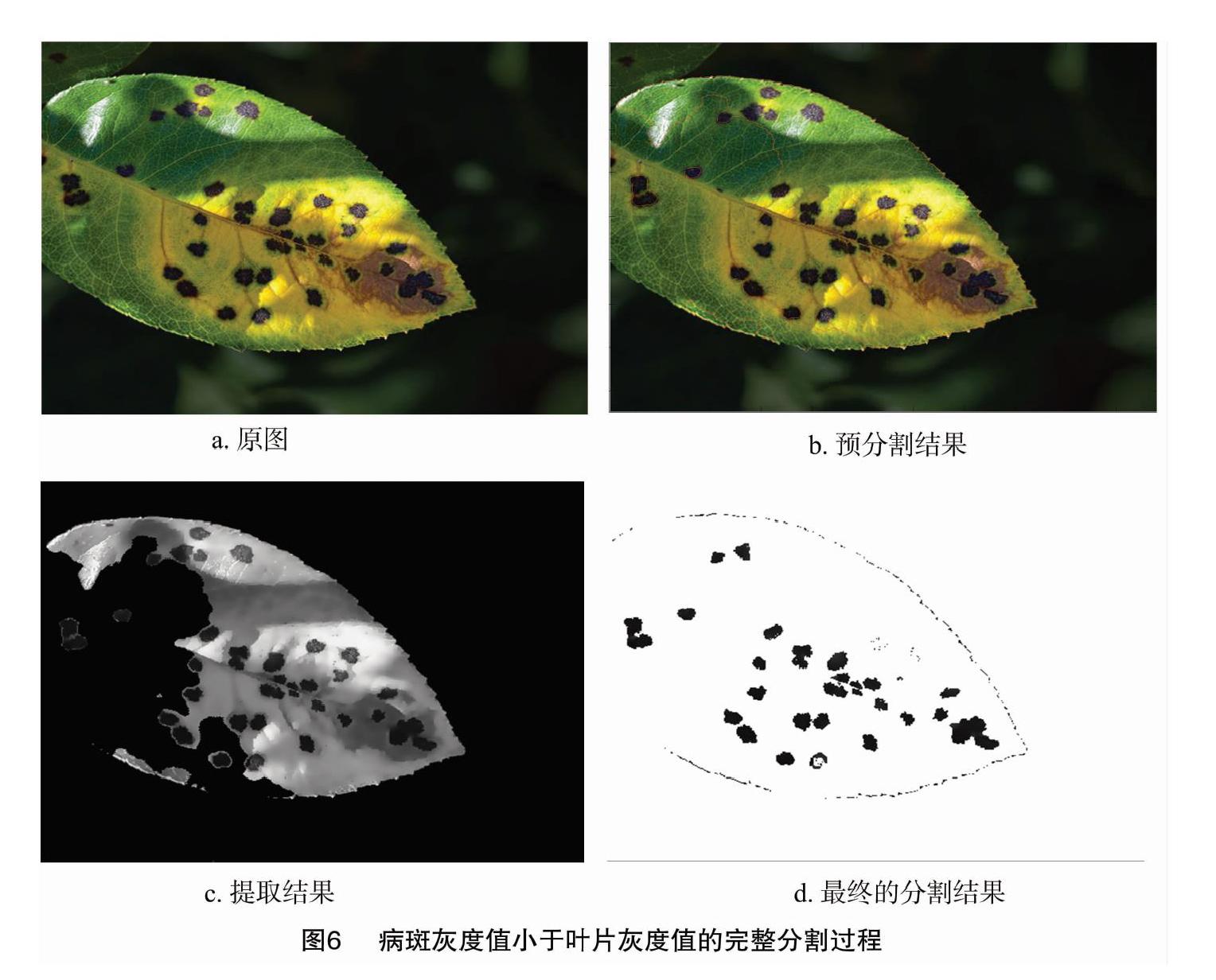
在另一个试验中，病斑的灰度值小于叶片的灰度值，完整的分割过程如图6所示。

为了更好地展现最终的分割效果，本研究将最终分割结果的背景设置为白色。用过漏检率（R1）、过检率（R2）来评估试验结果。作为试验结果的对比，本研究用基于高斯分布改进C-V模型对同样的图片进行分割[15]。对于基于高斯分布的C-V模型，笔者仔细选择参数，让其分割效果达到最好。

真实叶片病斑区域面积Sa由人工计算得到，算法分割出的病斑区域面积Sq通过size（data）得到，Si为Sa和Sq的交集区域。可以通过以下公式计算R1和R2：

R1=|Sa-Si|Sa;（15）

R2=|Sq-Si|Sa。（16）

由表1可知，用本研究提出的算法得到的R1和R2值远小于基于高斯分布改进C-V模型得到的R1和R2值，这说明本研究算法得到的分割结果准确度更高。

5 结论

为了解决复杂背景对于叶片病斑分割带来的过分割问题，本研究提出了两步分割的策略，通过加入各向异性扩散滤波器改造外部能量函数，得到了鲁棒性更强的AD-GAC模型，从而克服了GAC模型对噪声敏感的缺点。然后，通过提取预分割结果来去除复杂背景，将提取出来的像素灰度值作为一维数据，通过计算最大熵得到最佳阈值，将最终的病斑区域分割出来。试验结果证明，本研究提出的算法能有效地完成复杂背景下对叶片病斑的分割。

参考文献：

[1]Mai X C，Meng M Q H，Automatic lesion segmentation from rice leaf blast field images based on random forest[C]. RCAR，2016：255-259.

[2]Hu Q X，Tian J，He D J. Wheat leaf lesion color image segmentation with improved multichannel selection based on the ChanVese model[J]. Computers and Electronics in Agriculture，2017，135（C）：260-268.

[3]Zaitoun N M，Aqel M J. Survey on image segmentation techniques[J]. Procedia Computer Science，2015，65：797-806.

[4]Pratondo A，Ong S H，Chui C K，Region growing for medical image segmentation using a modified multiple-seed approach on a multi-core CPU computer[C]//The 15th International Conference on Biomedical Engineering，2013：112-115.

[5]Vincent L，Soille P，Watersheds in digital spaces：an efficient algorithm based on immersion simulations[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，1991，13（6）：583-598.

[6]Zhou S P，Wang J J，Zhang S，et al. Active contour model based on local and global intensity information for medical image segmentation[J]. Neurocomputing，2016，186：107-118.

[7]Kass M，Witkin A，Terzopoulos D. Snakes：active contour models[J]. International Journal of Computer Vision，1988，1（4）：321-331.

[8]Zeng L，Chen J，Xu Y F，et al. Level set method for image segmentation based on local variance and improved intensity inhomogeneity model[J]. IET Image Processing，2016，10（12）：1007.

[9]Csaelles V，Kimmel R，Sapiro G. Geodesic active contours[C]//Proceedings of IEEE International Conference on Computer Vision，1995：694-699.

[10]Perona P，Malik J. Scale-space and edge detection using anisotropic diffusion[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，1990，12（7）：629-639.

[11]Caselles V，Catt F，Coll T，et al. A geometric model for active contours in image processing[J]. Numerische Mathematik，1993，66（1）：1-31.

[12]Osher S，Fedkiw R. Level set methods and dynamic implicit surfaces[M]. New York：Springer-Verlag，2002：158-174.

[13]Li C M，Xu C Y，Gui C F，et al. Level set evolution without re-initialization：a new variational formulation[C]//IEEE Conf Comput Vis Pattern Recognit，2005：430-436.

[14]Long J W，Zhang J X，Xiang N，et al. An iterative maximum entropy thresholding algorithm[C]//2016 International Conference on Cyberworlds，2016：171-174.

[15]Tian J，Hu Q X，Ma X Y. Color image segmentation of plant lesion using improved C-V model based on Gaussian distribution[J]. Transactions of the Chinese Society of Agricultural Engineering，2013，29（16）：166-173.