天然硫化物矿物对地球深部热能的热电转化效应研究

贾昊凝，李 艳，黎晏彰，鲁安怀，丁●瑞

(造山带与地壳演化教育部重点实验室， 矿物环境功能北京市重点实验室， 北京大学 地球与空间科学学院，北京 100871)

地球系统中一切内生作用和表生作用的物质交换过程都需要能量。与受地球外部能量太阳光影响的地球表层系统不同，深部地球系统主要受到地球内部能量地热能的影响，在大地热流的影响下，地壳范围内形成了显著的地热梯度，地热能在多种热液环境下集中释放。相比太阳能主导的地球表生作用过程，人们对地球内部热能作用下的深部能量转化过程还远没有取得充分认识。

值得一提的是，矿物是介导地球物质与能量转化的关键载体之一，近十几年来，人们发现诸多金属硫化物矿物表现出良好的半导体特性，而且在地壳内分布广泛，尤其在地热能集中释放的热液区常常会形成堆积体或矿床。其中，一些禁带宽度较窄(小于1.20 eV)的半导体矿物已被证实具有优良的热电性能：黄铁矿(FeS2)可以用作热电转化材料(Wangetal., 2018)，并且Se、Co掺杂会使FeS2的电导率和塞贝克系数增大从而提高热电转化率(Uhligetal., 2014)；黄铜矿(Cu1+xFe1-xS2)具有理想的热电性能，并且在较低x值时具有较高的塞贝克系数(Angetal., 2015)；黝铜矿(Cu12Sb4S13)和斑铜矿(Cu5FeS4)额外的声子散射模式阻碍了晶格热传导过程，从而显著提高了其热电转换效率(Qiuetal., 2014; Chettyetal., 2015; Wyzgaetal., 2017)；具有金属阳离子缺陷的辉铜矿(Cu2-xS)中可自由迁移的Cu使其表现出极低的晶格热导率(Heetal., 2014)。这些天然半导体矿物因广泛存在晶格缺陷和杂质元素而成为非本征半导体，其原子振动产生的热能会使得价带或杂质能级上的电子被激发而产生跃迁形成自由载流子，其跃迁概率与载流子浓度随着温度升高而增加。当这些矿物处于地热梯度下时，载流子会发生扩散并在矿物内部形成热电场，使产生的热电子和热空穴能够进行有效迁移而形成传递通路，从而避免复合过程导致热量耗散，为温差电动势的形成与热载流子的高效流通提供得天独厚的条件。

本工作选取几种地壳热液区广泛赋存的天然硫化物矿物，通过X射线衍射(XRD)手段表征了其物相，通过热电性能评价系统、激光闪射法等测试技术测定了样品的热电半导体属性，根据热电基本理论和地热梯度构建模型评价了不同硫化物矿物产生的天然热电势、额外地电流以及热电转换效率，探究了天然半导体硫化物矿物热电转换效果的量化模型，并对地球内部热能的转化提出一种泛化量化方法，为进一步理解天然半导体矿物在地球系统能量转化过程中的载体作用提供了新论据，并为研究深部热能-电能转化对地球物质与能量交换过程的影响提供理论基础。

1 实验材料与方法

1.1 样品准备及物相表征

测试样品主要来自北京大学地球与空间科学学院地质博物馆馆藏硫化物样品(编号为1～6)，样品物相使用北京大学分析测试中心X射线衍射仪(X pertpro, Philips)鉴定，测试电压40 kV，测试电流40 mA，X射线源为Cu靶Kα1(λ=0.154 06 nm)射线，步长0.017°，扫描速度3°/min，扫描范围3°～90°。

1.2 电输运性质表征

将硫化物样品通过切割并抛光成尺寸约为3 mm×3 mm×8 mm的柱体，喷涂氮化硼作为防护层，在氦气氛围下使用UlvacRiko ZEM-3热电性能评价系统同时测量样品室温至最高758 K的塞贝克系数和电导率。

1.3 热输运性质表征

将硫化物样品切割并抛光为截面为6 mm×6 mm、厚1～2 mm的规格用于测量热扩散率。热导率由热扩散系数、定压比热容以及密度乘积得到，其中热扩散系数使用Netzsch LFA427在氮气氛围下激光闪光扩散法进行测量，定压比热容通过高温下晶态固体热容定律进行估算，密度由样品质量与体积确定。

2 结果与讨论

2.1 硫化物矿物物相分析

1～6号样品主要矿物物相分析结果如图1所示，各样品特征峰对应晶面已标注如图(ICDDPDF： 03-065-3321， 03-065-1573， 00-052-1516， 00-014-0323， 00-009-0328， 01-085-0599， 00-005-0592)。值得一提的是，由于Cu的亲硫性比Fe强，因此在硫逸度相对较低的热液环境下往往会产出较多含铜量较高的斑铜矿与辉铜矿，辉铜矿空间上往往与斑铜矿共生形成集合体，并有可能在近地表受到风化形成赤铁矿，因此对5号样品进行进一步热电性能表征将有助于对自然条件下硫化物矿物集合体的热电效应进行评估。

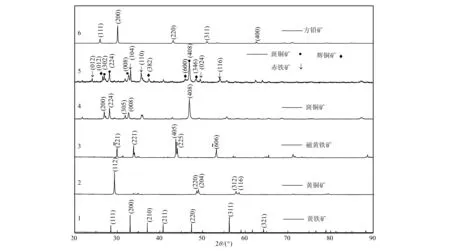
图 1 硫化物样品的XRD图谱Fig. 1 XRD patterns of sulfide samples

2.2 热电性能表征

热电测试选择300～760 K为温度测试区间，这有利于模拟地壳的地热梯度及局部的热异常。需要注意的是，斑铜矿与辉铜矿在测试温度区间内可能会发生相变(Heetal., 2014; Qiuetal., 2014)。斑铜矿473 K以下为四方晶系，473 K以上为等轴晶系。辉铜矿在376 K以下为稳定的斜方晶系，376～693 K为六方晶系，而高于693 K则转化为等轴晶系，这些与温度有关的相变有可能影响矿物的热电性能。

2.2.1 塞贝克系数分析

在热能-电能转换过程中，往往引入塞贝克系数S来衡量材料形成温差电动势的能力，可以将其表示为：

S=limΔΤ→0(ΔV/ΔT) (1)

其中，S为材料塞贝克系数，ΔV为产生电势差，ΔT为绝对温度差。若塞贝克系数为正，材料内部温差电动势方向由热端指向冷端；若塞贝克系数为负，则材料内部温差电动势方向由冷端指向热端。

通过测试前述矿物样品的塞贝克系数，可以发现除磁黄铁矿(样品3)的塞贝克系数很小而表现出金属性质以外，其它样品的塞贝克系数绝对值在测温区间保持在150～500 μV/K范围内(图2)，并且具有表现显著热电响应的潜质：黄铁矿在678 K下获得-271 μV/K的最大塞贝克系数；黄铜矿在473 K下获得-321 μV/K的最大塞贝克系数；斑铜矿在460 K下获得347 μV/K的最大塞贝克系数；方铅矿在461 K温度下获得-465 μV/K的最大塞贝克系数；斑铜矿-辉铜矿-赤铁矿集合体在接近室温的308 K下能够获得341 μV/K的最大塞贝克系数。值得一提的是，与样品具有相同化学组成的合成材料在相同测温区间的塞贝克系数也保持在100～500 μV/K，与样品的塞贝克系数大小相近(Johnsenetal., 2011; Qiuetal., 2014; Uhligetal., 2014; Angetal., 2015; Wangetal., 2018)。

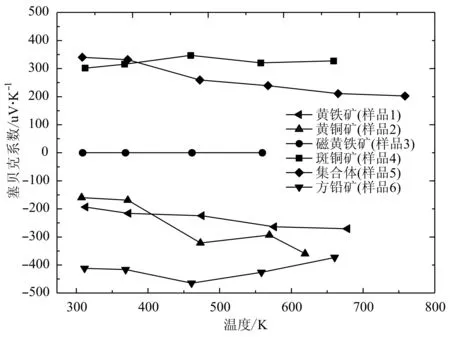
图 2 硫化物矿物样品随温度变化的塞贝克系数Fig. 2 Seebeck coefficients of sulfide mineral samples as a function of temperature

斑铜矿和斑铜矿-辉铜矿-赤铁矿集合体样品的塞贝克系数为正，呈现p型半导体特征，这说明空穴是其主要载流子，对应电子传输机制可能以价带电子跃迁至受主能级为主，高温端价电子获得足够能量跃迁至导带，成为能够导电的自由电子，价带留下的新空穴被临近共价键的价电子填补，填补造成的新空穴使得这一过程不断重复，从而相当于空穴作为载流子从高温端移动到低温端。相反，黄铜矿、黄铁矿和方铅矿则以电子为主要载流子，即电子作为多数载流子在温差条件下由高温端流向低温端，呈现n型半导体的特征。这些矿物中，天然掺杂的少量元素以异价类质同像形式代替矿物中的原子成为施主杂质，其多余的电子不参与形成共价键，在高温作用下容易脱离施主杂质的束缚，成为自由电子。

对含有杂质元素的半导体而言，塞贝克系数S可用下列公式表示(Heremansetal., 2008)：

从公式(2)中可知，塞贝克系数是一个与温度相关的物理量，受到载流子有效质量和载流子浓度的共同调控，随着温度升高，价带电子被激发跃迁至导带的概率增加，使得载流子的有效质量和浓度升高。在中低温条件下，载流子浓度主要由含量相对少的杂质原子贡献，塞贝克系数主要受载流子有效质量控制；在高温条件下，半导体本征激发占据主导，载流子浓度随温度升高急剧增加而成为主导因素。因此，在测试中，具有显著塞贝克系数的样品都可以观察到塞贝克系数与温度的相关关系。方铅矿(样品4)和斑铜矿(样品6)在测温区间的塞贝克系数变化趋势显示了塞贝克系数随温度升高先增加后减小的特性。

2.2.2 电导率及功率因数分析

样品电导率测试结果如图3所示。由于磁黄铁矿样品的电导率在103S/cm量级，呈现出具高电导率的金属特征，因此未在图中标出。从图中可以看出，在高温条件下，斑铜矿(样品4)及斑铜矿-辉铜矿-赤铁矿集合体(样品5)的电导率随温度升高而急剧增加，这可能与高温下本征激发带来的大量载流子有关。需要注意的是，黄铜矿样品表现出异常低的电导率，这可能与天然样品不够致密而存在的大量孔隙使得电阻过大有关。

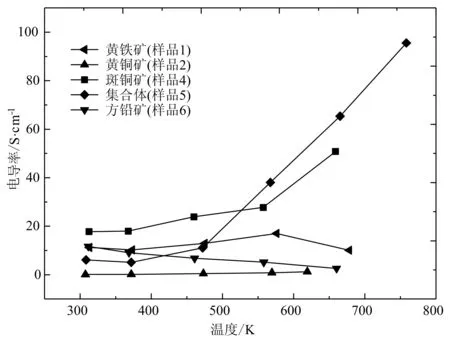
图 3 硫化物矿物样品随温度变化的电导率Fig. 3 Conductivity of sulfide mineral samples as a function of temperature

功率因数(Power Factor, PF)被用于评价热电材料的电输运性能，从而比较半导体矿物在确定温差条件下的热电性，其定义为：

PF=σS2(3)

其中σ为材料电导率，S为材料塞贝克系数。

半导体矿物样品的功率因数如图4所示。由于黄铜矿(样品2)的电导率低，磁黄铁矿(样品3)的塞贝克系数低， 两个样品的电输运性能不够理想而表现出低功率因数。其它硫化物半导体矿物样品由于具有可观的功率因数， 例如斑铜矿(样品4)和集合体样品(样品5)在高温条件下分别具有约545 μW/(m·K2)和390 μW/(m·K2)的高功率因数，方铅矿(样品6)在近似地表温度条件下表现出198 μW/(m·K2)的高功率因数，在相应的不同地热梯度条件下具有产生天然热电流的潜能。

图 4 硫化物矿物样品随温度变化的功率因数Fig. 4 Power factor of sulfide mineral samples as a function of temperature

2.2.3 热导率分析

热导率由热扩散系数、密度、定压比热容决定。由于各类硫化物矿物的热容在本次实验测温区间变化不大(Grønvold and Westrum, 1962, 1976; Grønvoldetal., 1987; Heetal., 2014; Qiuetal., 2014; Xieetal., 2017; Liuetal., 2018)，即热导率测试的温度区间要大于其德拜温度，样品热容趋于常数，因此，假设固体定压热容(Cp)与定容热容(Cv)相等，此时可以使用经典热容定律估算样品定压热容，即恒压下元素的原子热容为：

Cp=3NKB(4)

其中，N为阿伏伽德罗常数，KB为玻尔兹曼常量。

化合物分子热容约等于构成该化合物各元素热容之和：

C=Σnici(5)

其中，ni为化合物中元素i的原子数，ci为该元素的摩尔热容。

热导率测量结果如图5所示。需要说明的是，方铅矿样品在热导率测量过程中信号较差，考虑到其样品物相组成较单一，故在后文的模拟计算中引用文献数据(Johnsenetal., 2011)，其热导率参数在此不列出。热导率测量结果表明，磁黄铁矿(样品3)、斑铜矿(样品4)及集合体(样品5)表现出显著的低热导率，这可能与磁黄铁矿、斑铜矿与辉铜矿的特殊结构有关。辉铜矿和斑铜矿等热电材料已被证明具有类似“声子液体”的结构特征，即硫原子构成刚性有序的骨架结构，阳离子及空位在间隙位置无序分布，而由于其间隙位置势垒较低，空位的存在使阳离子能够在热激发条件下自由迁移，从而产生额外的横波阻尼阻碍热传导(Qiuetal., 2014; Heetal., 2014)。磁黄铁矿晶胞中Fe2+、Fe3+以及空位的无序分布可能也起到了类似效应从而导致其热导率明显低于与其化学成分类似的黄铁矿。

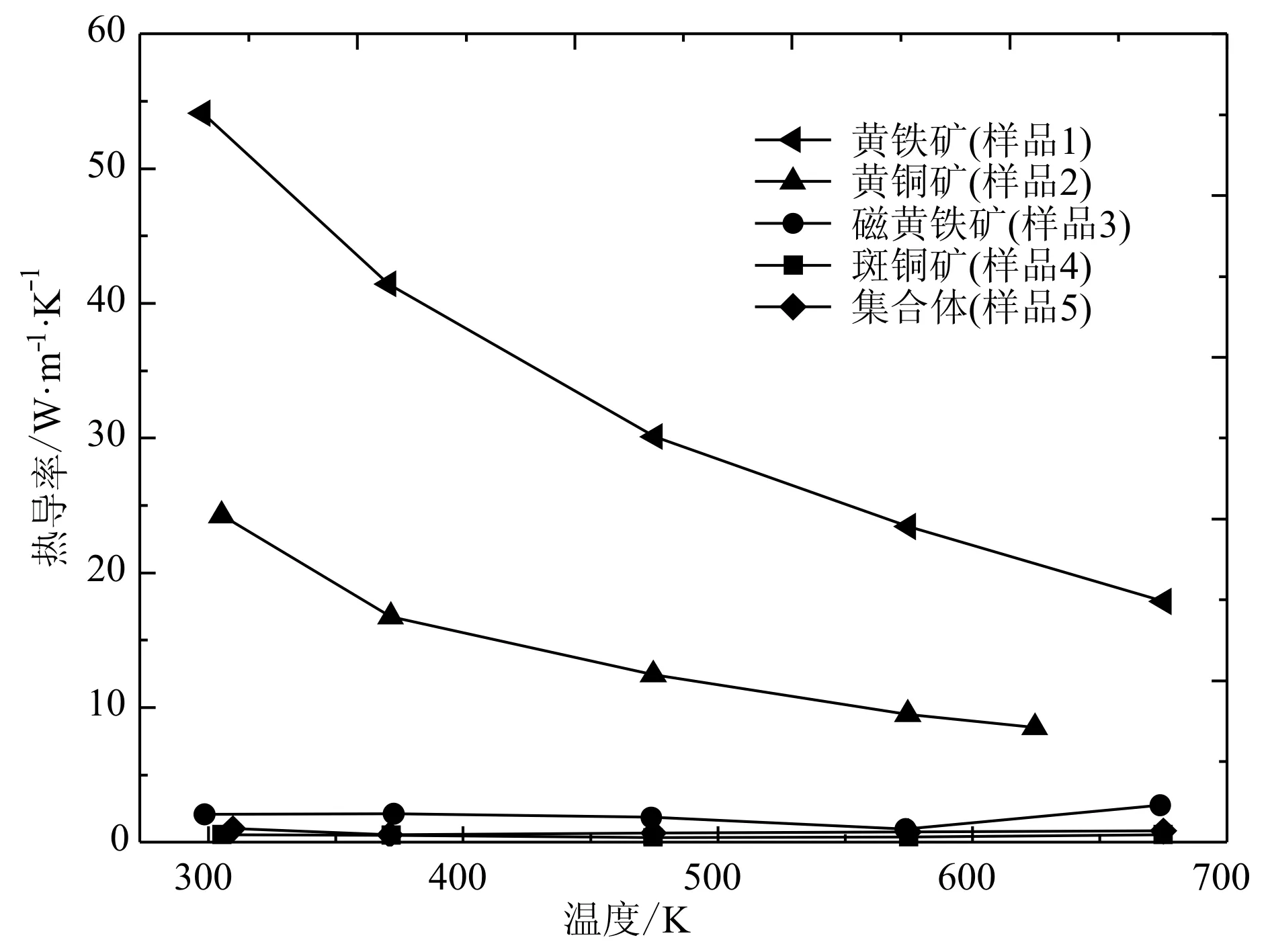
图 5 硫化物矿物样品随温度变化的热导率Fig. 5 Thermal conductivity of sulfide mineral samples as a function of temperature

3 天然地热梯度下热电效应模拟计算

热液活动导致地壳内部局部热异常区往往存在显著的局部温度梯度，如羊八井地区就出现有46.5 ℃/km的温度梯度(佟伟等， 1981)，说明该地区地壳中热液活动活跃，这为天然硫化物半导体矿物在地温梯度下产生显著热电效应提供了前提条件。基于热电基本理论，可以对天然地热梯度下硫化物半导体矿物产生的热电势、地电流及其热电转化效率进行相应估算。

3.1 地热梯度下天然热电势模拟计算

由于半导体矿物高温端的热激发作用较强，空穴或电子浓度也比低温端高，载流子在这种浓度梯度的驱动下会在半导体内部向低温端扩散，从而形成电势差实现热电转换。根据热电基本理论，假设硫化物矿物是单一均质的半导体，可以大致估算其产生的天然热电势(U)：

其中，T1和T2分别代表冷、热端的绝对温度，S(T)表示对应温度T下材料的塞贝克系数。

在最理想条件下，可以根据某一矿物的塞贝克系数-温度曲线和冷、热两端温度T1和T2，大致估算某一温度场条件下单一矿物体能够产生的天然热电势值。假设相邻两个测试温度之间塞贝克系数发生线性变化，以300 K作为冷端温度，根据公式积分求出几类硫化物半导体矿物产生的相对热电势(UH)-热端温度变化曲线(图6)，从而求出某一温度场下单一矿物体能够产生的天然热电势U：

U=UH(T2)-UH(T1) (7)

其中，UH(T1)和UH(T2)分别为冷端和热端温度对应的相对热电势值。

需要注意的是，自然条件下矿物集合体的组成并非是单一的。假设矿物集合体作为均匀混合相的塞贝克系数为各相塞贝克系数的加权平均值，不考虑不同种矿物对载流子产生与传导的影响，可以根据各类硫化物半导体矿物的百分含量n来估算矿物集合体产生的天然热电势U：

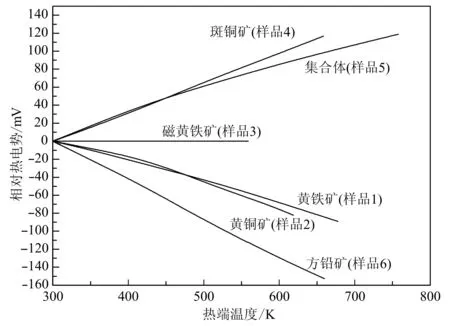
图 6 相对热电势值随热端温度变化曲线Fig. 6 The curve of relative thermoelectric potential value as a function of the hot end temperature

U=ΣniUi(8)

其中ni为硫化物半导体矿物i在矿物体中的百分含量，Ui为硫化物半导体在该温度场条件下产生的热电势。

在自然条件下矿物堆积体的组成具有显著的物相差异，则两种不同物相组成的单一矿物体的接触点处由于塞贝克系数的差异而存在电势差ΔU：

ΔU=Ua(T)-Ub(T) (9)

其中，Ua(T)和Ub(T)为硫化物半导体a和b在温度T下的天然热电势值。

热电矿物体在一定温差条件下可以近似看作一个偶极电流源(Shenetal., 2010)。以n型半导体矿物为例，热端载流子浓度较大，电子作为主要载流子向冷端扩散并聚集，并在热端留下相应空穴，使正负电荷发生分离,因此受热电矿物体影响，在地表两个观测点可以检测到额外的电势差。由于点电荷电场中某点的电势与介质的介电常数和其距离点电荷距离呈反比，如图7矿物体产生的天然热电势U与地表两个观测点之间的电势差V可以表示为：

U=q/2πε0l(10)

V=(q/4πε1)(1/rH1+1/rH2-1/rC1-1/rC2) (11)可见U和V之间有如下关系：

V=(U1ε0/2ε1) (1/rH1+1/rH2-1/rC1-1/rC2) (12)

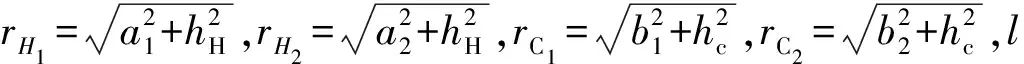
图 7 地表观测热电矿物产生热电效应示意图Fig. 7 Schematic diagram of thermoelectric effect of thermoelectric minerals by surface observation

3.2 地热梯度下半导体硫化物产生的额外地电流

根据热电矿物的偶极电流源模型和电场强度的定义，我们可以计算地表观测点1受矿物体热、冷端电荷影响的电场强度大小EH和EC：

则观测点在地表平面可观测到的电场强度E的大小可表示为：

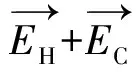
2abEHECcosθ/rHrC]1/2(15)

其中，θ为矿物热、冷两端地面投影点与观测点连线的夹角，且有cosθ=(a2+b2+c2)/2ab。

该观测点产生的地表电流密度J可以表示为：

J=σ1E(16)

σ1为观测点地表介质电导率。

3.3 地热梯度下硫化物半导体矿物的天然热电转换效率

热电效应使半导体矿物的冷、热两端具有一定的电势差，因此当天然半导体矿物与导电矿物接触构成回路时，就能在地热梯度下构成回路形成电流，实现热能-电能的转化。在实际的天然热电转换中，电能转化自部分热传导过程传递的热能，计算硫化物矿物最大热电转化效率可以用来衡量吸收转化天然地热能的能力。

假设硫化物半导体矿物体的温度梯度从热端指向冷端，且垂直于温度梯度方向的硫化物半导体矿物体和导电矿物体截面积相等，本应全部通过热传导过程传递能量的功率W0可以表示为：

其中，k(T)表示温度T下硫化物半导体矿物的热导率，A表示矿物体的截面积。

热电矿物与导电矿物构成回路的总电阻R为：

R=l(ρ1ave+ρ0ave)/A(18)

其中，ρ1ave和ρ0ave表示硫化物半导体矿物和导电矿物的平均电阻率，且有ρ1ave=1/σ1ave，ρ0ave=1/σ0ave，σ1ave和σ0ave为二者平均电导率。

硫化物半导体矿物在与导电矿物构成回路后的电功率W1和热电转换率η可以表示为：

W1=U2/R(19)

当导电矿物的电阻率远低于硫化物半导体矿物的电阻率时，可以忽略导电矿物电阻得到最大热电转换率ηmax:

因此，若以300 K为冷端温度，各硫化物半导体矿物ηmax随热端温度变化关系如图8所示。由图8可以看出，斑铜矿和斑铜矿-辉铜矿-赤铁矿集合体样品得益于低热导率和高温下的高电导率，在650 K热端温度下的最大热电转换率可达4‰和2.2‰，其它硫化物半导体矿物的热电转换率虽然较低，但其在稳定地热梯度条件下长期存在的热电效应也极有可能对地球内部热能的转化产生重要影响。

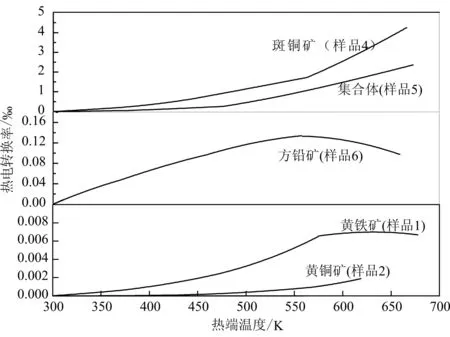
图 8 硫化物半导体矿物热电转换率随热端温度变化Fig. 8 Thermoelectric conversion rate of sulfide semiconductor minerals as a function of the hot end temperature

4 结论

天然硫化物半导体矿物具有良好的热电输运性能，除磁黄铁矿表现为金属导体的电输运性质以外，天然斑铜矿和斑铜矿-辉铜矿-赤铁矿集合体为p型半导体，黄铁矿、黄铜矿和斑铜矿为n型半导体，在约300～700 K范围内具有显著的塞贝克系数，能产生显著的热电响应。斑铜矿及矿物集合体样品的低热导率和在高温下的高电导率使其具有优良的热电输运性能。

在地热梯度下的天然热电势计算结果显示硫化物半导体矿物能够在约300～700 K温差条件下产生100 mV左右的天然热电势，具有产生显著温差电动势的能力并可以通过偶极子电流源模型的计算，将天然热电势和地表观测到的热电势、额外的地表电流密度建立联系。

硫化物半导体矿物在某一温差条件下的最大热电转换率可由天然热电势作用下硫化物矿物电功率与热传导功率的比值得到，经过估算发现，硫化物半导体矿物在在300～650 K温差条件下具有可观的热电转换率，尤其斑铜矿能够产生的最大热电转换率可达4‰，这对理解自然条件下地球内部热能的能量转换具有重要意义。