矿区高强度开采地表损坏动态预测模型

闫伟涛，陈俊杰，柴华彬，颜少鸽

（河南理工大学测绘与国土信息工程学院，焦作454003）

0 引 言

地下资源开采不可避免会引起地表沉陷，地表不同沉陷指标的大小都会影响到地表耕地、建（构）筑物等地表附着物的安全使用，如下沉易导致高潜水位地区地表积水，水平变形导致地表产生拉伸型裂缝或挤压型隆起，严重破坏原有耕地的土壤结构，造成耕地农作物减产甚至绝收，这种现象在矿区尤其严重[1-5]。根据矿区开采沉陷相关知识[6-8]，地表沉陷指标大致可分为两大类：静态指标和动态指标。静态指标主要包括下沉、水平移动等移动量和倾斜、曲率、水平变形等变形量，动态指标主要指静态指标在单位时间内的变化量，如下沉速度、水平移动速度等。目前，国内外学者对静态指标研究的较多，且取得了很多研究成果并得到了很好的实际应用[6-15]。但对于下沉速度等动态指标则研究的较少，且很多学者对下沉速度的研究是在下沉速度曲线符合正态分布这一假设的基础上进行的[6,8,16]。而现场实测资料发现，地表下沉速度曲线并不符合正态分布规律，采用正态分布函数构建下沉速度预测模型将产生较大的预测偏差。这一问题在高强度开采条件下表现的更加突出。高强度开采的主要特征是开采深厚比小，宽深比大，推进速度快[4,15-17]。高强度开采地表和覆岩移动剧烈、破坏严重，地表下沉速度曲线偏态严重[18-27]。所以本文以高强度开采工作面为研究对象，选取下沉速度这一动态沉陷指标，分析地表下沉速度曲线形态和下沉速度的时空分布规律，并据此给出地表下沉速度的动态预测模型。研究结果可为充分开采阶段的地表动态剧烈损坏区域的确定及其修复时机的把握提供理论支持。

达到充分采动后，下沉速度达到该地质采矿条件下的最大值，工作面继续推进，下沉速度曲线形态基本保持不变，且曲线与工作面的相对位置基本不变，下沉速度曲线有规律的向前移动。而其他开采时段的下沉速度曲线分布则无此明显的规律性。所以本文仅对充分采动阶段的下沉速度曲线分布规律进行分析研究。

1 高强度开采地表下沉速度曲线形态实测分析

选取2407高强度开采工作面为研究对象。2407工作面地处陕北黄土高原与毛乌素沙漠的接壤地带，地表起伏不大且全部为风积砂所覆盖。工作面平均采深131 m，其中松散层42 m，煤层倾角1°～3°，设计采高5.2 m，工作面走向长3 224 m，倾向长284 m，工作面推进速度约15 m/d。煤层结构简单，为稳定性煤层。上覆岩层为中硬偏硬岩层，老顶为粉细砂岩，直接顶为中细砂岩，直接底为砂质泥岩。采用全部垮落法管理顶板。在2407高强度开采工作面停采线一侧地表沿走向布设地表移动观测站，测点间距15 m，采空区内、外观测线长分别为210 m和120 m，如图1。对观测站每隔一天测量一次。图2 为获得的三期充分开采阶段的下沉速度数据。正态分布的峰度系数为3.0，偏度系数为0。峰度系数小于3.0，则说明观测量集中度低；偏度系数越大，则说明分布的对称性越差；偏度系数大于0 时，分布为右偏。对图2 中的3 期下沉速度曲线进行正态分布的适合度检验，结果显示下沉速度曲线的峰度系数介于0.1～0.5 之间，偏度系数介于1.1～1.2 之间，由此可知，下沉速度曲线为右偏偏态分布。结合工作面开采实际情况，可知下沉速度曲线偏向采空区一侧，即采空区侧下沉速度曲线较陡，工作面侧下沉速度曲线较缓。

图1 2407工作面观测站布置示意图Fig.1 2407 face layout of ground station

图2 实测下沉速度曲线Fig.2 In-suit subsidence velocity curve

2 高强度开采地表下沉速度时空分布规律的模拟分析

最大下沉速度往往滞后于工作面推进位置一段距离，滞后距离被称为最大下沉速度滞后距。但最大下沉速度滞后距是个几何概念，未能从沉陷机理上对滞后现象进行解释。所以本文通过对“地下开采—顶板冒落—覆岩破坏—地表沉陷”这一沉陷发育过程建立时空域上的井上下联系，来研究高强度开采下沉速度的时空分布规律。

2.1 模型的建立

本文参照2407 工作面地质采矿条件，进行相似模型试验。模型架尺寸为4 000 mm×300 mm×1 500 mm。根据相似理论，试验设计模型几何相似系数为1：100，时间相似系数为1：10，容重相似系数为0.6，强度相似系数为0.006。试验选用沙、碳酸钙、石膏和水为原料根据岩性选用对应的配比号制作模型。岩层各层选用的配比号见表1。

根据神东矿区2407 高强度开采工作面地质采矿条件进行相似模拟试验，对其覆岩破坏方式进行探讨。模型几何比例尺为1：100，模型中煤层厚5.39 cm，上覆岩层131 cm，其中基岩89 cm，松散层42 cm。煤岩层水平铺设，每次开挖15 cm。模拟开挖结束后覆岩破坏如图1所示。

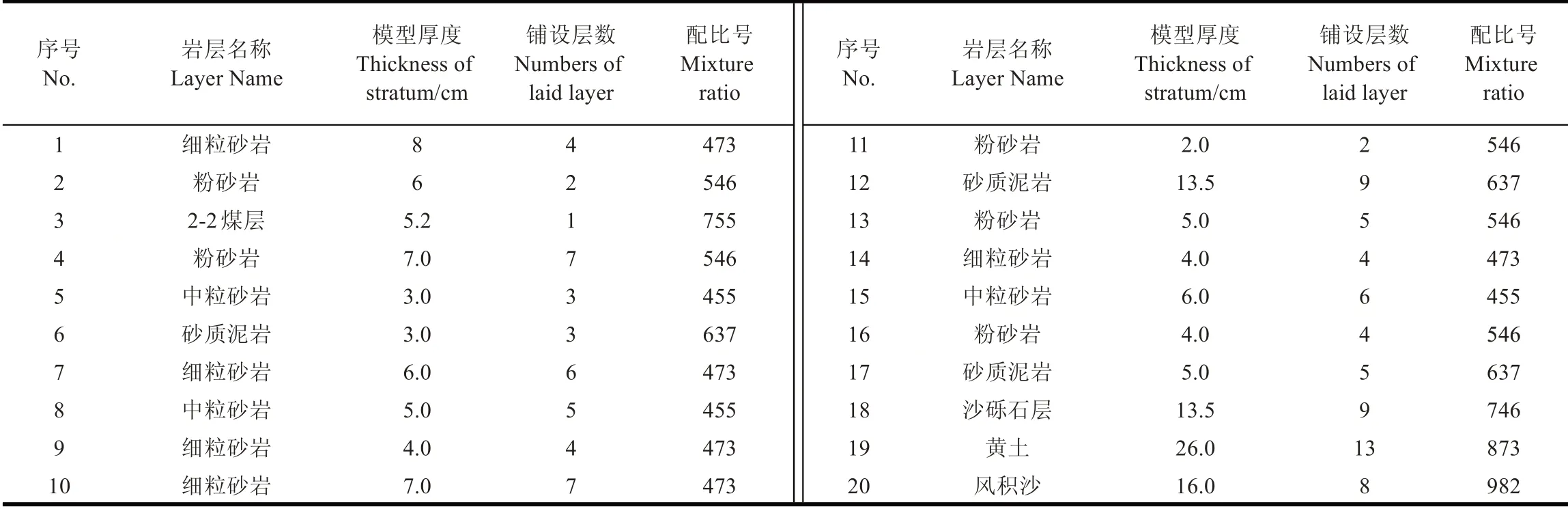
表1 模型相似材料配比及用量表Table 1 Proportion and dosage of similar material for model

2.2 下沉速度时空分布规律的分析

模型制作完风干后，进行模拟开挖。最终覆岩破坏形态如图3所示。

从图中可看出，基岩主要沿着基岩破断角方向发生全厚破断，松散层的破坏类型主要为剪切破坏，破坏方向为垂直向上。覆岩移动稳定后，停采线及开切眼处覆岩破坏最外边界为两条近似直线的裂缝迹线，覆岩破坏主要发生于边界线之间，边界线和水平线之间在采空区一侧的夹角称为基岩破断角。图3说明，高强度开采基岩破坏沿基岩破断角方向向上发展，松散层破坏近似以垂直方向向上发育，直达地表，形成台阶型裂缝。模型试验测得工作面推进位置处基岩破断角为54°～57°，取其平均值56°。

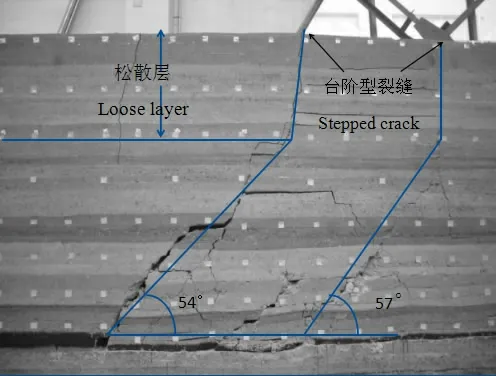
图3 相似模拟试验覆岩破坏状态Fig.3 Damage state of overlying strata after simulated excavation

地表台阶型裂缝的出现瞬间改变了原有地表下沉速度场的分布。高强度开采工作面的顶板垮落、地表台阶型裂缝发育和地表下沉速度分布的相关信息见表2。

表2 地表下沉速度空间分布规律分析Table 2 Spatial distribution law of surface subsidence velocity

结合相似模拟实验，由表3 可知，顶板垮落、覆岩破坏和地表下沉速度分布三者之间具有如下关系（如图4）：

1）最大下沉速度位于台阶型裂缝处，二者的位置可由工作面推进位置和基岩破断角实时确定；

2）地表下沉速度动态分布具有周期性，且与顶板岩层垮落和台阶型裂缝的周期相同。

由上可知，最大下沉速度发生于台阶型裂缝处，二者的位置可由工作面推进位置和基岩破断角实时确定。所以高强度开采最大下沉速度滞后于工作面推进位置的距离可由式（1）计算。

式中：L 为最大下沉速度滞后距，m；Hj为基岩厚度，m；γ为基岩破断角，°。

3 高强度开采地表损坏动态预测模型的建立

3.1 预测函数选择的合理性分析

由上节可知，高强度开采下沉速度曲线符合右偏偏态分布规律，故选取的函数应满足以下两个条件：（1）右偏偏态性；（2）归一性。现分别对选取的对数正态密度函数进行分析。

1）对数正态分布密度函数的右偏偏态性[28]

对数正态分布密度函数表达式如下：

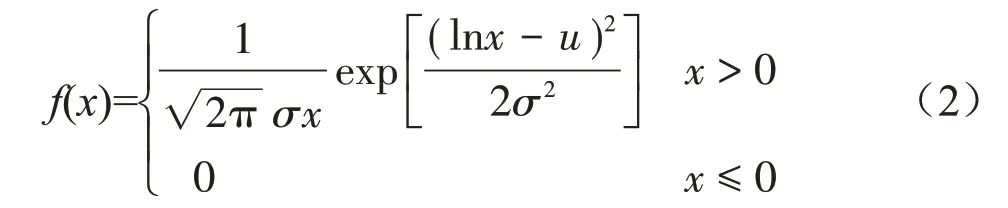
式中：x为随机变量，u为lnx的期望值，σ为lnx的标准差。

图4 地表下沉速度动态分布与覆岩破断关系井上下对照图Fig.4 Location map of relationship between surface dynamic subsidence distribution and overlying rock breaking

对数正态分布密度函数的极大值为：

均值为：

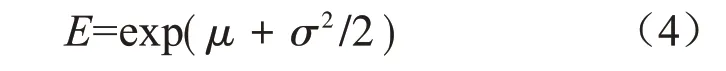
通过对比式（3）和式（4），可知，

故对数正态分布密度函数的极大值小于均值，极大值在均值的左侧，所以对数正态分布密度函数为右偏态。

2）对数正态密度函数的归一性

对对数正态密度函数在(-∞,+∞)进行积分，过程如下：

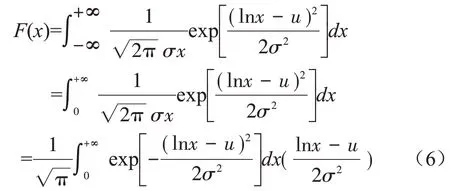
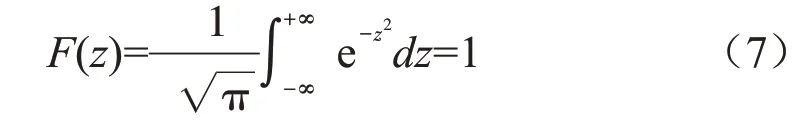
综上，对数正态密度函数满足右偏偏态性和归一性两个条件，故选取对数正态密度函数构建下沉速度动态预测模型具有一定的合理性。

3.2 地表损坏动态预测模型的构建

在无大地质构造和地表起伏存在的条件下，充分采动阶段各个时期的下沉速度曲线在形态、极值和与工作面的相对位置等方面都具有相似性。充分采动阶段内各个时期的下沉速度曲线可看作某一时刻的下沉速度曲线随工作面推进在工作面推进方向上的整体平移。平移量等于两个时刻最大下沉速度点之间的距离。设有如图5所示的坐标系统。坐标原点位于开切眼正上方对应的地表点上，横坐标轴x 沿工作面推进方向布设，且沿工作面推进方向为正，纵坐标轴v(x)竖直向上为正，代表横坐标为x的地表点的下沉速度值。

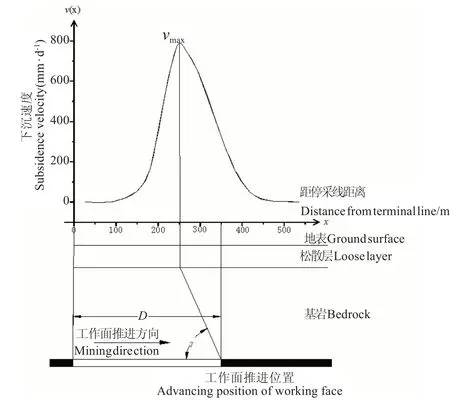
图5 坐标系的建立Fig.5 Establishment of coordinate system

最大下沉速度点在坐标系中的位置可由下式确定：

式中：D 为工作面推进距离，m；Hj为基岩厚度，m；γ 为基岩破断角，（°）。

两个时刻最大下沉速度点之间的距离d可由下式计算：

式中：xvm1、xvm2分别为时刻1 和时刻2 最大下沉速度点离开切眼的距离，m；D1、D2分别为时刻1和时刻2工作面的推进距离，m。则由式（9）可知，充分采动阶段任两个时刻最大下沉速度点之间的距离等于该段时间工作面的推进距离。

假设某一充分采动时刻获得工作面的下沉速度实测数据，通过拟合得出该时刻的下沉速度预测模型如下:

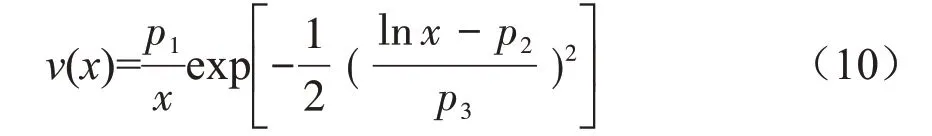
式中：v(x)为横坐标为x 的地面点的下沉速度值，mm/d；p1、p2、p3为模型参数。

自该时刻起，工作面又回采距离d 时的地表下沉速度预测模型如下：

4 地表损坏动态预测模型的实例精度验证

4.1实例一

以哈拉沟2407 工作面为例，以2014 年1 月6 日的地表实测下沉速度数据进行非线性曲线最小二乘拟合求取预测参数。得到的预测方程如下：

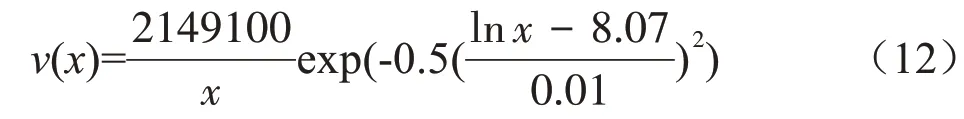
预测参数：p1=2149100，p2=8.07，p3=0.01。

然后将预测参数带入预测模型式（11），对后续地表下沉速度进行预测。2014年1月8日和2014年1月10日两个时间点的预测与实测结果对比分析见图6和表3。

图6 不同日期的地表下沉速度曲线对数正态分布预测结果Fig.6 Logarithmic normal distribution fitting result of subsidence velocity with different time

表3 下沉速度预测效果Table 3 Fitting result of subsidence velocity

4.2 实例二

选用相邻的补连塔矿某高强度开采工作面实测数据对模型进行应用分析[29-30]。工作面走向长3592 m，倾向长300.5 m，煤层倾角1°～3°，采高4.5 m，平均采深200 m，上覆岩层岩性为中硬偏硬。采用综合机械化长壁开采方法进行开采，平均开采进度为12 m/d，完全垮落式方法管理顶板。为进行岩移观测，在工作面开切眼一侧布设半条走向观测线，煤柱上方布设观测线长度380 m，采空区上方布设观测线长度500 m，测点间距为20 m（煤柱上方区域）和30 m（采空区上方区域）。选取走向观测线充分采动时期内工作面推进133、210、300 和350 m 四个时间点的地表下沉速度实测数据进行模型的应用分析。

采用工作面推进133 m 时的实测数据非线性曲线拟合求取预测参数，非线性拟合曲线拟合方程如下：

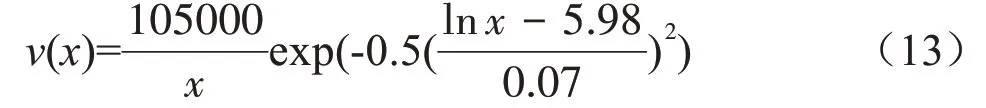
拟合预测参数:p1=105000，p2=5.98，p3=0.07。

然后将预测参数带入预测模型式（11）对后续地表下沉速度进行预测。工作面推进210、300 和350 m 三个时间点的预测与实测结果对比分析见图7和表3。

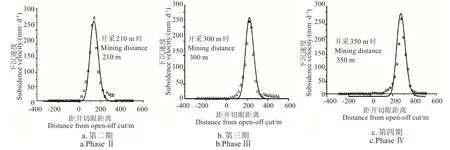
图7 不同推进距离时的地表下沉速度曲线对数正态分布预测结果Fig.7 Logarithmic normal distribution fitting result of subsidence velocity with different advance distance of working face

由图6、图7和表3分析可知，采用对数正态模型预测时，预测和实测曲线的决定系数在0.9 以上，标准差与实测最大下沉速度值的比值小于7.0%，说明对数正态密度函数适于建立下沉速度预测模型，且模型预测值与实测值相差较小，模型预测精度高，较为符合现场实际。

5 结 论

1）分析了高强度开采下沉速度曲线的偏态性。根据2407 工作面走向主断面实测数据资料，总结了下沉速度曲线的右偏偏态分布规律。

2）揭示了高强度开采覆岩的破坏规律。高强度开采下，基岩沿基岩破断角方向发生全厚破断，松散层沿着垂直方向发生剪切破坏。

3）研究了下沉速度的时空分布规律。根据高强度开采工作面充分采动阶段的现场实测资料和相似模拟实验，综合分析了工作面开采地表下沉速度的动态分布特点：地表下沉速度动态分布具有与顶板岩层垮落和台阶型裂缝相同的周期性；最大下沉速度点位置可由工作面推进位置和基岩破断角实时确定。

4）建立了下沉速度的动态预测模型。采用对数正态密度函数构建了下沉速度动态预测模型。经实例验证，预测和实测曲线的决定系数在0.9以上，标准差与试测最大下沉速度值的比值小于7.0%，结果表明预测模型较为符合现场实际。