阵元数对组合线阵近场目标定位性能的影响*

李昆鹏 康春玉 夏志军 张闻龙 张 亿

（1.海军大连舰艇学院学员五大队 大连 116018）（2.海军大连舰艇学院水武与防化系 大连 116018）

1 引言

随着降噪技术的不断发展，水下目标辐射噪声级不断降低，隐蔽性随之增强。近场区域警戒和近海岸的港口防御等军事需求越来越迫切［1～2］。针对近场声目标定位问题，聚焦波束形成是常见的方法之一，其原理就是根据目标声源到各个阵元曲率半径不同，补偿球面波传播模型下的时延差，并对补偿后的阵元信号进行加权求和，聚焦波束形成输出会出现峰值，其峰值所应的角度即为目标信号的方位。科研人员基于均匀线列阵，对近场聚焦波束形成方法展开了比较深入的研究，2010年，熊鑫等［3］系统地研究了基于线列阵的最小方差无失真响应（Minimum Variance Distortionless Response，MVDR）聚焦波束形成方法，仿真结果表明，MVDR聚焦波束形成方法能够有效解决因线阵阵元间距增大而导致的“混叠”问题，提高了聚焦空间分辨率。2014年，刘凯等［4］提出了一种基于矩阵空域预滤波处理的近场聚焦波束形成方法，该方法有效提高了对弱辐射噪声目标的定位能力，进一步优化了聚焦波束形成方法，从目前的研究情况来看，基于单线阵的近场目标的定位研究主要集中于方位估计或方位与俯仰角估计，且仍然无法解决“左右舷模糊”等问题。针对基于空间阵的目标距离、方位、俯仰角三维同时定位需要进行更深入的研究。研究也表明，定位性能与基阵的布设、定位的方法等都有比较大的关系，如何设计更合理的小尺寸基阵实现对近场目标的准确定位仍然是需要解决的问题［5～6］。

本文提出组合线阵设计的构想，推导了组合线阵的接收信号模型，提出了近场三维声聚焦波束形成的实现框架，通过对切割球面上聚焦点的扫描，得到目标方位角和俯仰角，再通过对不同扫描球面上最大输出功率的比较得到目标距离，从而实现了对近场目标距离、方位角、俯仰角的估计，并采用常规波束形成方法仿真分析了组合线阵阵元数对目标三维定位性能的影响，可为组合线阵的阵形设计提供一定支撑。

2 组合线阵近场信号接收模型

如图1所示，组合线阵由4条线型子阵组成，每条子线阵的阵元数为m，则整个基阵的总阵元数M=4m。4条线型子阵与水平面的倾斜角度均为θz，单条子阵的长度为d且阵元间距相等，以四条线阵的对称中心为圆心建立坐标系，每条线阵距离圆心均为l1，假设近场声源S的位置为( )r，θ，φ ，其中r表示声源到参考点的距离，θ表示俯仰角，φ表示方位角。声源 S 到第 k（k=1，2，...，4）条子阵第 i个（i=1，2，...，m）阵元的距离为 rki。

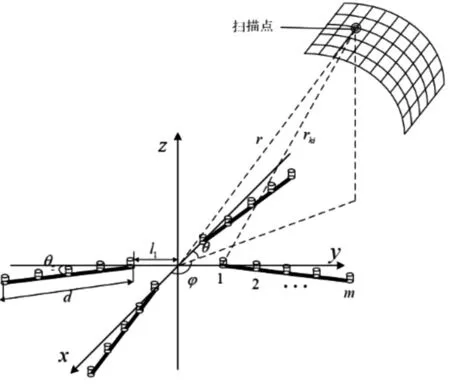
图1 组合线阵阵列模型

根据和几何关系，运用三角形余弦定理可得

第 k（k=1，2，...，4）条子阵第 i个阵元收到信号与参考点的时延差为

则第 k（k=1，2，...，4）条子阵第 i个阵元的接收信号可表示为

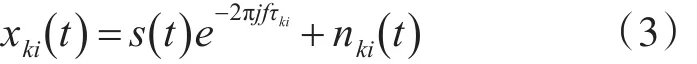
表示为矩阵形式为

3 三维声聚焦波束形成原理

常规聚焦波束形成，就是根据目标声源到各个阵元曲率半径不同，补偿球面波传播模型下的时延差，并对补偿后的阵元信号进行加权求和，聚焦波束形成输出会出现峰值，其峰值所应的角度即为目标信号的方位，其传统方法的时延差是声源距离和方位的二维函数，在扫描平面上对不同位置点进行扫描，获得该平面的声强图，当扫描点与目标位置重合时，聚焦波束形成输出会出现峰值，即可得到目标的距离和方位估计［7～10］。

本文在常规聚焦波束形成的基础上，提出三维声聚焦波束形成方法。

首先，以坐标系原点为中心，将搜索目标的距离范围切割为Q个扫描球面，每个扫描球面的半径差为10m，对每一个扫描球面rq再以1°为间隔，将扫描球面 rq划分为181×361个扫描点［11～12］。

对rq（扫描球面距参考点的距离）球面上扫描点进行均匀加权常规波束形成，可得到波束输出为

加权向量：

相应rq球面上各个扫描点的输出功率为

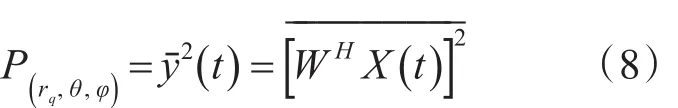
利 用 上 式 ，代 入 不 同 的(θ ，φ ) ，其 中θ=-90°～90°，φ=0°～360°，就可扫描出 rq球面上最大输出功率，然后通过扫描不同球面rq，得到每个球面的最大输出功率，通过比较不同球面的最大输出功率，得到输出功率的最大值Pmax，其所对应的球面距离即为目标声源的估计距离r，同时此球面上出现最大输出功率的扫描点所对应的角度即为目标声源的方位角和俯仰角。

4 仿真数据检验与分析

仿真验证中假设单条线阵长度d固定为3m，线阵倾斜角度θz为15°，每条子阵上的阵元均匀分布，半径l1为1.5m，信号采样频率 fs为12.5kHz，快拍数为4096，信噪比SNR设为5dB，声传播速度c为1500 m/s。每次仿真实验都进行100次蒙特卡洛实验。

4.1 阵元数对测距性能的影响

实验一：假设目标俯仰角为5°，方位角为90°，目标为频率500Hz的单频率信号，单条线阵阵元数从3变化到48，目标距离从500m变化到2000m时，目标距离估计相对误差的三维和二维图如图2所示。

从图2可以看出，单条线阵阵元数对不同距离目标下的距离估计误差影响比较大，总的来看，阵元数越多，同一距离目标的距离估计就越准确，即测距性能越好。同一阵元数下，目标距离越远，估计误差就越大。同时通过取值分析可以得到，当单条线阵阵元数大于30时，2000m范围内目标的距离估计误差均小于20%。

图2 不同阵元数下的目标距离估计相对误差

实验二：假设目标俯仰角为5°，方位角为90°，目标距离为2000m，单条线阵阵元数从3变化到48，目标仍为单频信号，频率从500Hz～1500Hz线性变化，不同阵元数下，不同频率目标的距离估计相对误差的三维和二维图如图3所示。

从图3可以看出，单条线阵阵元数、信号频率都是影响距离估计误差的重要因素，总的来看，阵元数越多，使得同一频率目标的距离估计越准确，测距性能越好，与仿真实验一得到的结果一致。另外，同一阵元数下，目标信号频率越高，距离估计误差越小。同时通过取值分析可以得到当频率大于1000Hz时，距离估计误差可均小于20%。

4.2 阵元数对聚焦空间分辨率的影响

实验一：假设目标方位角为60°，距离为2000m，信号为频率500Hz的单频信号，单条线阵阵元数从3变化到48，目标俯仰角从-90°变化到90°，不同单条线阵阵元数、不同俯仰角下的俯仰角聚焦空间分辨率如图4所示。

图3 不同阵元数下的目标距离估计相对误差

图4 不同阵元数下的俯仰角聚焦空间分辨率

由图4可以看到，俯仰角在-15°～15°范围内的目标，其俯仰角聚焦空间分辨率明显差于其它位置。对于同一俯仰角的目标，单条线阵阵元数越多，俯仰角聚焦空间分辨率越高，但不是特别明显。

实验二：假设目标俯仰角为 5°，距离为2000m，信号为频率500Hz的单频信号，单条线阵阵元数从3变化到48，目标方位角从0°变化到360°，不同单条线阵阵元数、不同方位角下的目标方位角聚焦空间分辨率如图5所示。

从图5可以看出，单条线阵阵元数越多，目标方位角聚焦空间分辨率越高。同一阵元数下，不同方位目标的聚焦空间分辨率基本相同。通过取值分析，当单条线阵阵元数大于3时，方位角聚焦空间分辨率均小于5°。

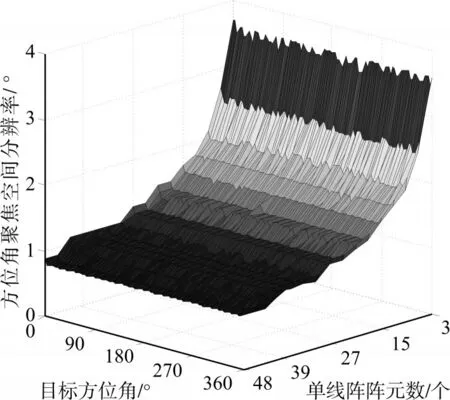
图5 不同阵元数下的方位角聚焦空间分辨率

实验三：假设目标距离为2000m，俯仰角为5°，方位角为60°，单条线阵阵元数从3变化到48，目标仍为单频信号，频率从500Hz～1500Hz线性变化，不同单条线阵阵元数下，不同频率目标的俯仰角聚焦空间分辨率如图6（a）所示，方位角聚焦空间分辨率如图6（b）所示。

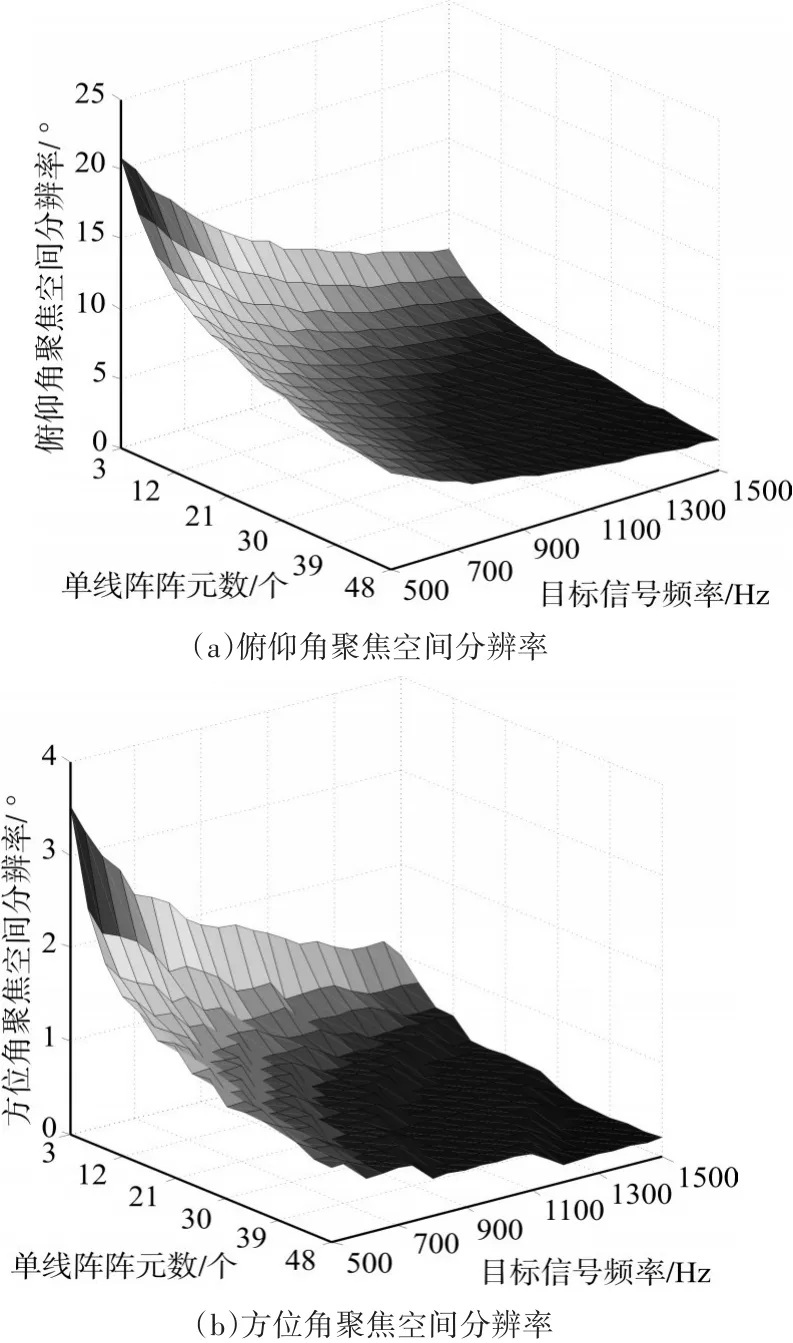
图6 不同阵元数下聚焦空间分辨率曲线图

从图6（a）可以看出，单条线阵阵元数不变，信号频率越高，俯仰角聚焦空间分辨率值越小，分辨目标能力越强。目标信号频率不变，线阵阵元数越多，俯仰角聚焦空间分辨率值越小，分辨目标能力越强。通过取值分析，当要求俯仰角聚焦空间分辨率小于5度时，单条线阵阵元数必须多于30个。

从图6（b）可以看出，单条线阵阵元数不变，信号频率越高，方位角聚焦空间分辨率值越小，分辨目标能力越强。信号频率不变，线阵阵元数越多，方位角聚焦空间分辨率值越小，分辨目标能力越强。同时可以看到，方位角聚焦空间分辨率明显高于俯仰角聚焦空间分辨率，当单条线阵阵元数大于3时，方位角聚焦空间分辨率均小于5°。

综合图4～图6可以看出，总的来说，阵元数越多，对聚焦空间分辨率都有好处，但由尺寸限制，每条线阵的阵元数不可能无限增大，在设计这样的基阵时，每条线阵上的阵元数应尽可能多。当指标要求方位和俯仰角聚焦空间分辨率均小于5°时，每条线阵上阵元数至少应大于30。

5 结语

本文推导了组合线阵近场信号接收模型和三维声聚焦波束形成方法，研究了组合线阵近场常规三维声聚焦波束形成被动定位的性能，从仿真数据分析发现，当固定线阵倾斜角度、线阵与圆心的距离l1和每条线阵的长度时，每条线阵上布设的阵元数对定位性能的影响比较大，阵元数越多，测距性能越好，聚焦空间分辨率越高。当指标要求距离估计相对误差小于10%，方位和俯仰角聚焦空间分辨率均小于5°时，每条线阵上阵元数至少应大于30个。需要说明的是，本文仿真实验的目标信号均为窄带信号，对宽带目标信号的定位性能还有待进一步分析验证，同时，组合线阵子阵条数、组合线阵的中心半径l1、每条线阵的长度等对定位性能的影响也需要进一步研究。