基于M/D/c排队模型的机场管道加油任务分配问题研究*
2019-11-28林贤隆
林贤隆 陈 智
(1.陆军勤务学院 重庆 320311)(2.空军勤务学院 徐州 221000)
1 引言
战时航空兵部队战机出动架次密集,场站保障力量面临威胁严重,战场情况复杂,突发情况多,对场站后勤保障提出了更高的要求,如何科学高效地完成后勤保障,是在提高战斗力时面临的一大问题。而油料保障作为航空兵后勤保障的重要因素,其保障效率直接影响了整个后勤保障的效果。战时油料保障可能无法完全按照既定的保障计划进行,可能出现因保障任务重而无法按时完成的情况,具体来讲就是战机落地后要进入等待队列而无法立即进行加油作业。在这种情况下,飞机等待加油的情况可以模拟为多服务台排队模型。
针对飞机油料加注问题应用排队论的研究,主要集中在机场建设时管道加油口的设置方面,顾毓等[1]通过建立多队列多服务台的形式模型并通过仿真来确定管道加油口的最优数量;施毅等[2~3]研究了基于三阶段法建立管道和油车两种加油系统的仿真模型,为机场加油平台系统改造合理配置提供了科学的方法,同时基于事件调度法建立了系统的仿真模型,明显提高了军事、经济效益;陆朝荣等[4~5]应用单队多列排队论模型,采用面向事件法,通过VFP语言进行仿真,实现了机场管道加油系统的优化设计。此外,排队论在军队领域的应用主要集中在装备保障维修[6],军事信息[7],通信频率分配[8],应急医疗[9~10]等方面。
一般排队模型假设服务台可以不间断工作,既不失效也不休息,而实际情况中,由于一般情况下机场油库的油料储备较为充足,且加油口可以连续工作,故可以把管道加油系统也看作经典排队模型系统,本文利用排队论的方法,建立了管道加油排队模型,并得出在一定作战任务中的不同机场管道加油保障强度大小,为下一步作战及保障计划提供依据。
2 管道加油排队模型分析
2.1 模型描述
排队是人们生活、工作和学习中十分常见的现象,即顾客为了某种服务目的到达服务地点,因不能立即获得服务而进入队列。在实际作战中,航空兵场站对作战飞机进行油料保障,由于出动强度大、作战飞机着陆间隔时间不确定等问题,往往会形成排队现象。
机场管道加油系统主要由过滤操作设备、泵及调速系统、环形管、加油地井或接头、加油管等构成。飞机所需燃料油由管道输送到加油地井或接头,并通过加油管加入飞机,加油压力由泵及调速系统进行控制。当前机场管道加油系统可以做到根据加油井开设数量来对泵的工作压力进行自动调节,从而使加油井的压力保持基本不变。因此,可以看作服务台的服务能力始终不变。依据管道加油特点,结合排队论一般模型,建立管道加油排队模型如图1所示。
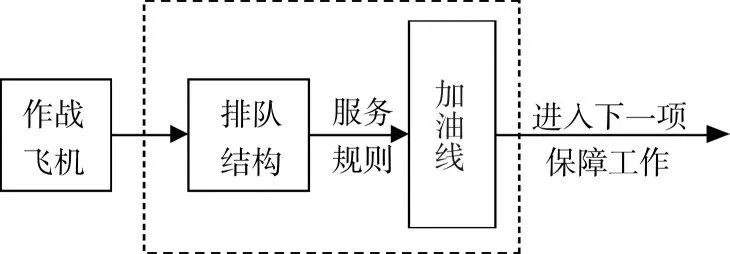
图1 管道加油排队模型
2.2 模型假设
一般的排队系统都有三个基本组成部分:输入过程、排队规则和服务机构[11]。排队模型根据输入过程、排队规则和服务机构的不同,分为很多类别,Kendall记号表示为X/Y/Z/A/B/C。其中,X表示顾客相继到达时间间隔的分布;Y表示服务时间分布;Z表示服务台的个数;A表示服务系统的容量;B表示顾客源的数目;C表示服务规则。本文根据战时飞机管道加油实际情况,对飞机到达、对待加油飞机的规则和管道加油能力按照排队系统的三个组成部分作出如下假设。
2.2.1 输入过程
即指飞机到达加油线服从什么样的分布。在作战时,飞机单机飞行或双机、四机编队飞行,易形成单架或批次不规律、不等距着陆,同时飞机到达时间与飞行时间、架次相关。在不相重叠的时间段内飞机到达数是相互独立的,并且在瞬时内只能有一架飞机到达(降落)。故在t时间段内到达n架飞机的概率Pn(t)符合泊松分布,即

则飞机依次到达的间隔时间的概率分布为负指数分布M。
2.2.2 排队规则
飞机加油作业一般服从先到先服务(First Come First Serve,FCFS)规则。
2.2.3 服务机构
即指同一时刻有多少加油口可以进行加油,对每一飞机补油时间遵从什么规律。管道加油系统为多服务台并列系统,加油口数量一定,每一加油口给同一机型加油时间基本相同。
综上所述,该排队系统符合排队论中M/D/c/N/N/FCFS模型。
3 建立管道加油排队模型
3.1 主要指标
Pn为系统中有n架飞机的概率;队长Ls为系统中的飞机总数;排队长Lq为队列中正在排队等待的飞机数;逗留时间Ws为飞机在系统中的停留时间;等待时间Wq为飞机在队列中的等待时间;λ为系统中新飞机的平均到达率,即飞机到达强度;D为单个加油口给一架飞机补油时间。根据单机所需补油量Ei和加油速率vi确定,D=Ei/vi;μ为单个加油口加油率,即加油强度,μ=1/D=vi/Ei;ρ为加油繁忙率 ρ=λ/cμ。
相互关系的Little公式:
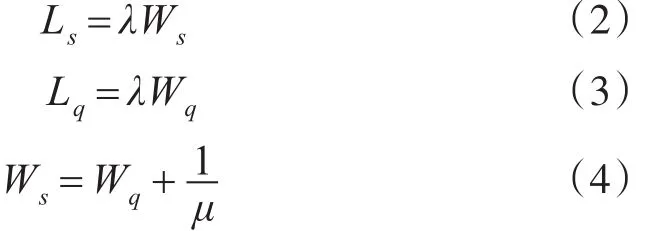

根据排队理论可知当cμ<λ时,流程将随着时间的增加,将出现无限队长,此种情况不作探讨,只假设cμ>λ,不会排成无限队列,系统平均到达率等于离去率,达到平衡状态。
3.2 M/D/c模型的计算求解
M/D/c模型的求解方法国内文献较少且其中有谬误之处。参考国外关于排队论的著作,简要介绍其求解过程[12]。设系统中稳定情况下,在t时刻有j架飞机的概率为 pj,则
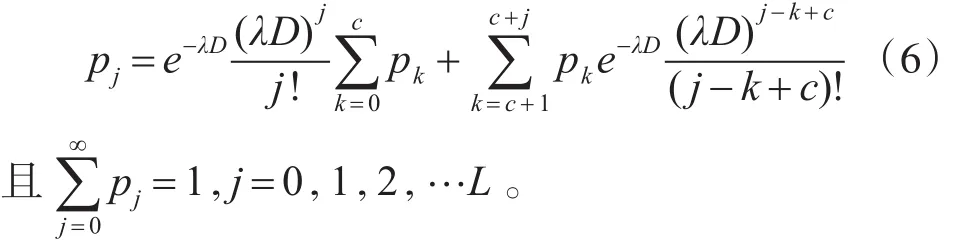
根据Little公式,pj满足如下关系:

进而得出
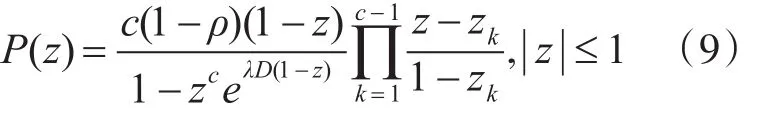
由此可求得当(k-1)D≤x<kD,k=1,2,…,时的平均等待时间

同时可求得队长:

由求解出的Wq、Lq,根据Little公式,进而可求得其他指标。
4 实例分析
假设空军A场站应用管道加油系统进行保障,共有6个加油口可用,单个加油口加油能力为1000L/min,在某小时需保障36架次某型战斗机作战行动,该型战斗机每次需补油7000L。
B场站有8个加油口可用,单个加油口加油能力为1200L/min,在某两小时需保障90架次某型战斗机作战行动,该型战斗机每次需补油7000L。
即:
EA=7000L;vA=1000L/min;cA=6;λA=36/1=36/h
EB=7000L;vB=1200L/min;cB=8;λB=90/2=45/h则:
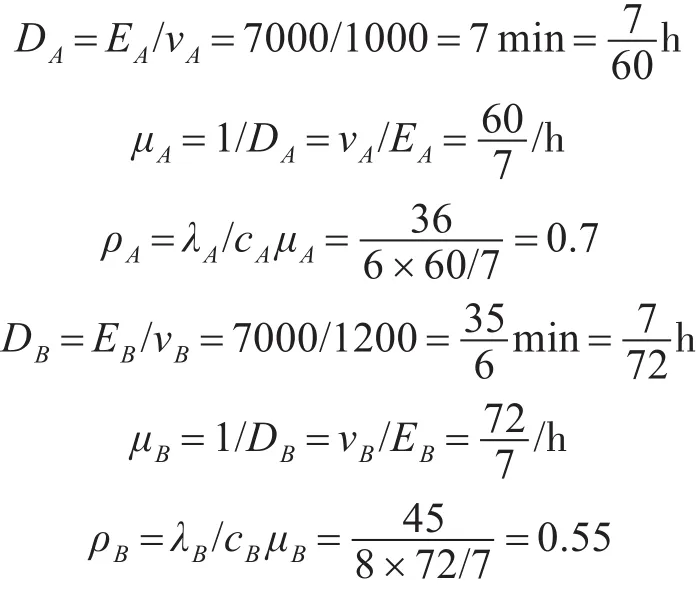
通过上文求解公式,得到相关指标如下:


表1 加油能力结果
从表1可以直观地看出,B场站加油能力相对于作战任务来讲比较充足,而A场站相对来讲加油能力稍弱。在作下一步的任务分配时,可以从以下几方面考虑:
1)根据作战计划,可将临近场站作战任务适当调整到B场站;
2)安排油料支援保障力量时,可适当向保障任务相对重(平均等待时间长)的场站倾斜;
3)在留有备用力量的前提下,可将保障任务轻的场站保障力量(油车等)向任务较重的场站进行支援。
5 结语
为更科学地分析场站管道加油能力,本文建立了基于M/D/c排队论的管道加油能力模型,并给出了M/D/c排队模型的基本解法,计算出平均等待时间和平均等待架数,最后通过实例分析,对不同场站、不同任务的管道加油能力进行统一分析,并得出结果,为指挥员科学决策提供依据。
