基于MEMS传感器的惯导系统预处理和姿态解算
2019-11-27王明杭朱志宇
刘 维,王明杭,朱志宇
(江苏科技大学电子与信息学院,江苏 镇江 212003)
随着MEMS传感器技术的飞快发展,MEMS器件以其成本低、尺寸小、功耗低等优势逐渐被人们用到IMU领域,如在无人机、航姿参考系统、水下机器人、单兵导航等领域都有较为广泛的应用[1],故本文探讨的基于MEMS传感器的惯导系统预处理和姿态解算是有重大意义的。
捷联惯性导航系统(SINS)是不依靠外界信号,也不会向外界辐射信号的一种自主导航系统[2]。但是MEMS陀螺仪存在常值漂移,加速度具有零偏,而磁力计容易受到周围环境的干扰,工作较长时间后这些器件会产生很大的误差,造成姿态角的解算精度下降[3]。针对惯性器件误差问题,文献[4]等,解决的方法是建立IMU的误差模型,使用卡尔曼滤波等算法求出误差模型参数,以达到误差补偿目的,但建立准确的误差模型和滤波时选对参数,存在计算量大的问题为了改进姿态角解算精度,文献[5]设计出一种互补滤波的姿态融合算法,动态试验下,滚动角误差小于2.3°,俯仰角误差小于3.1°,航向角误差小于4°。精度不是太高。文献[6]是直接对姿态角进行补偿,首先推导并建立姿态角的误差方程,使用EKF等算法求出误差参数,以达到误差补偿目的,此方法姿态解算的精度高,满足测姿要求,但是推导的姿态角的误差方程比较繁琐,而且状态方程非线性,使用EKF需要计算雅可比矩阵,计算量加大,不利于实际使用。
本文设计一种基于优化自适应无迹卡尔曼滤波的姿态解算方法,在MEMS惯性传感器经过预处理的基础上,利用优化AUKF高精度特性,消除噪声干扰提升姿态角解算的精度,进行了静态预处理实验和姿态解算跑车实验,分别验证了预处理的效果和姿态解算的性能。
1 SINS姿态角的解算过程
SINS的姿态角解算的具体过程如图1所示,SINS是采用三轴加速度计、陀螺仪和磁力计分别测量载体的加速度、角速率和地磁场变化信息。由于MEMS传感器测得值易受到误差的干扰,造成姿态解算精度不高。为了得到较准确的姿态角信息,所以先对惯性器件测得值进行预处理,之后建立姿态角解算模型,再使用优化AUKF算法进行姿态角计算。

图1 SINS姿态角的解算过程
2 传感器数据的预处理


图2 MEMS传感器预处理过程
2.1 陀螺仪误差模型
使用时间序列分析法对MEMS陀螺仪随机误差进行分析,建模之前先对采集数据进行去除偏移量和滤波处理后,将平稳、正态分布的随机误差用ARMA(p,q)模型表示[7]:
(1)
式中:xt为时间序列;φp是自回归系数;θq滑动平均系数;εt为残差,p,q为ARMA模型阶次数[7],一般情况下,陀螺仪的温漂误差模型阶数都不是太高,通常小于或等于三阶,取p=2,q=1,采集100个陀螺仪随机误差信号点(Z轴),使用最小二乘法进行曲线拟合,得到其表达式:
xt=0.761 8xt-1+0.064 56xt-2-εt-0.977 4εt-1
(2)
2.2 加速度计误差模型
采用一元高阶多项式模型对MEMS加速度计信号进行建模补偿[8],利用最小二乘法对不同阶的模型参数拟合。首先采集静止状态下的100个加速度计误差信号点(X轴),最小二乘法拟合的不同阶模型参数如下:

表1 MEMS加速度计模型参数
设计一元高阶模型时,通过调节模型的阶次,对比补偿前后加速度计的误差,发现阶次越高补偿效果越好,四阶以上的补偿效果近似,故采用一元四阶模型对加速度计误差进行补偿,具体模型如下:

(3)
3 基于优化AUKF的姿态解算
3.1 姿态角的提取
根据参考文献[9]的姿态角微分方程可以使用下式表示:
(4)

(5)
式中:m=[mx,my,mz]T是磁力计的测量值。f=[fx,fy,fz]T是加速度信号。把式(4)求出的姿态信息对上式求得姿态角进行补偿即可。
3.2 姿态角解算过程
为得到三个姿态角准确解算结果,选用三个姿态角作为状态变量X=[θφψ],建立滤波状态方程为:
(6)
式中:[wθwφwψ]T为系统的过程激励噪声向量。通过姿态算法解算出来的姿态角为Zk=[θkφkψk],可以反映出姿态角的变化可是实时性较低,故当作观测量来更新系统的状态,则观测方程为:
(7)
式中:vk=[vθkvφkvψk]T是观测噪声向量。
4 优化AUKF算法
4.1 普通UKF存在的问题
第一,自适应问题。UKF相比较于EKF有较高精度,但是在实践过程中,当UKF滤波器在选取初始值时,若初始值存在误差干扰时,肯定会影响最优的结果[10-11]。第二,鲁棒性差。在实际的工作中,在噪声的驱使或干扰下,会造成滤波器的精度和稳定性下降。第三,对系统模型的结构问题,当系统模型存在误差较大时,滤波器通过状态最优估计消除噪声和使用自适应因子对协方差进行缩放,但是效果不是很理想。
4.2 自适应因子的选取
影响自适应无迹卡尔曼滤波器性能的关键因素是自适应因子的选取,自适应因子ak与系统的协方差矩阵和残差有关,初值为1,它的取值范围是0≤ak≤1。如果ak取值合理,则它能够平衡系统模型预测信息与测量信息之间的权比。ak按下式构造:
(8)

4.3 状态噪声自适应处理
当系统的模型误差和外部噪声比较大时,若只是依靠上面的自适应因子进行衰减,得到的最优状态估计值并不是很理想,为得到准确的状态值,需要对状态噪声做进一步的自适应处理。若观测方程为线性的,假设在加性噪声的干扰下,在滤波的过程中,状态的协方差可以表示为:
(9)
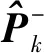
(10)
在最优估计状况下,dk为期望值0的高斯白噪声[12],对两边取方差得:
(11)
根据上式引入缩放因子为:
(12)
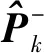
(13)
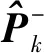
5 实验结果与分析
为了验证预处理方法的效果和姿态解算的结果,本文进行了实验。实验使用基于某型号的MEMS微传感器的捷联惯导系统,高精度的光纤惯导(GIF6536A)并把它输出姿态角当作真值,在室外远离磁干扰的地方进行下面实验。
5.1 预处理实验
采集固定好的MEMS陀螺仪信号,以5 Hz连续采集5 min,对其输出信号进行去除偏移量和滤波处理,处理后的角速度信号正态检验如图3所示。
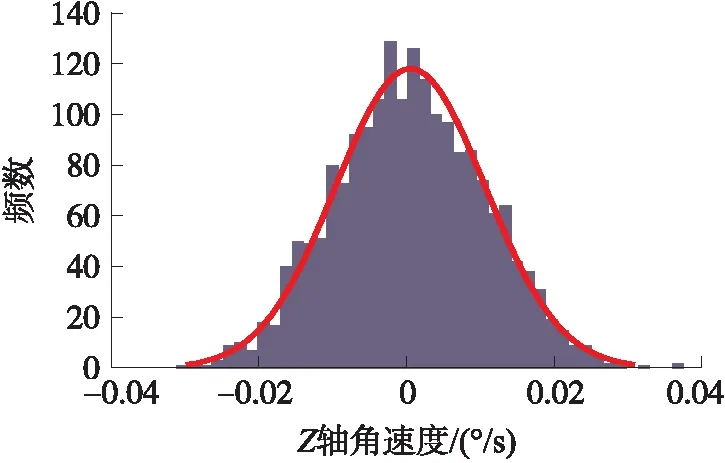
图3 陀螺仪数据处理
图3为静态时陀螺仪的Z轴输出,可以看出处理后的信号是一个平稳、正态分布的随机序列。再由式(2)的ARMA模型,建立Kalman滤波器,参数设置如下:

式中:Φk,k-1是tk-1到tk时刻的转移矩阵,Γ是系统噪声矩阵,Q是过程噪声协方差。得到的Kalman滤波前后的陀螺仪Z轴静态随机误差如图4和表2所示。

图4 静态实验结果

实验数据滤波前滤波后加速度计均值0.000 240.000 21信号/g标准差0.001 100.000 31陀螺仪信号均值-0.001 84-0.000 87/(°/s)标准差0.007 900.001 80
同样根据式(3)描述的加速度误差模型,进行Kalman滤波,滤波前后的加速度计信号误差如图5和表2所示。

图5 加速度计的信号预处理
根据图4和图5可以很清楚的看到,经过Kalman滤波后的陀螺仪和加速度计误差信号的变化幅度明显较小。通过表2的MEMS传感器误差信号滤波前后的均值和标准差对比,也可以看出Kalman滤波后的信号分散程度明显变小,其中滤波后的信号标准差比滤波前信号小了一个数量级,进一步说明预处理效果较好。
5.2 姿态解算跑车实验
为验证姿态角解算的精度,进行跑车实验,本实验以高精度的光纤惯导的姿态数据为基准数据(真值)。将实验系统与高精度的惯导并排安装在实验车上,开动试验车,两套实验系统同时测量试验车的姿态信息,从开始到试验车停止进行10 min左右的时间,车载实验实物图如图6所示。把系统解算的姿态角与高精度惯导的姿态角做差得到动态实验的姿态角误差结果见图7~图9所示,表3为三种不同的滤波算法产生的姿态误差数据分析。

图6 车载实验实物图

图7 滚动角误差

图8 俯仰角误差
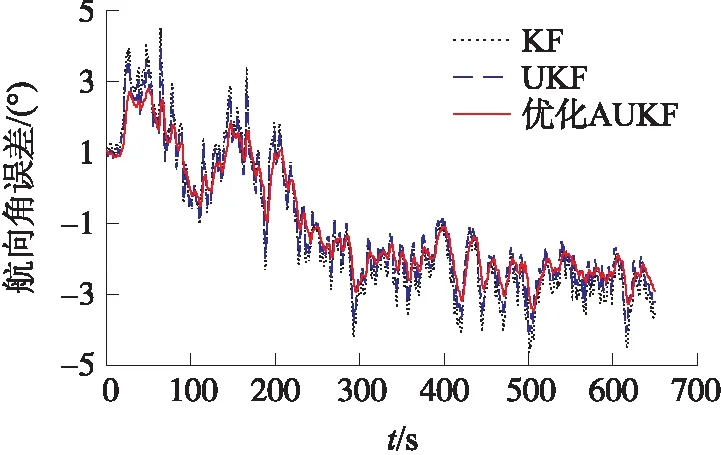
图9 航向角误差
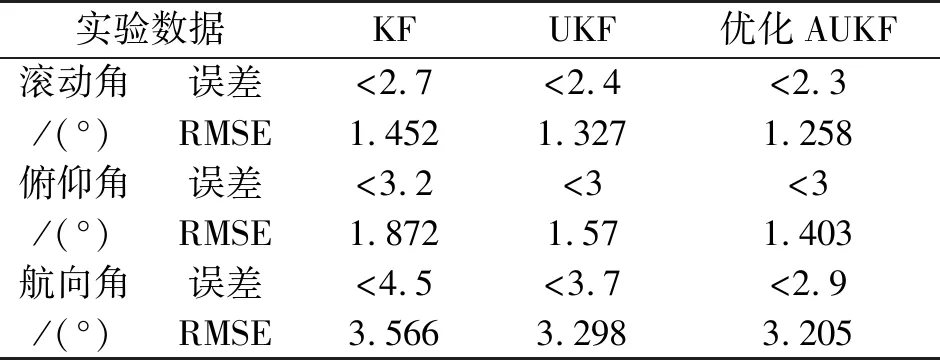
实验数据KFUKF优化AUKF滚动角误差<2.7<2.4<2.3/(°)RMSE1.4521.3271.258俯仰角误差<3.2<3<3/(°)RMSE1.8721.571.403航向角误差<4.5<3.7<2.9/(°)RMSE3.5663.2983.205
从图7~图9和表3可以得到,动态实验下采用优化AUKF解算得到的滚动角误差小于2.3°,俯仰角误差小于3°,航向角误差小于2.9°,相比KF和UKF产生的姿态角误差减小很多。同时计算动态实验下姿态角的均方根误差(RMSE),采用优化AUKF算法得到的滚动角、俯仰角和航向角的RMSE分别为 1.029°、1.493°和2.762°,通过表3中的数据和图7~图9,可以看出采用优化AUKF算法相对于KF、UKF可以得到较高的姿态角解算精度,效果明显。
6 结论
本文设计一种基于优化自适应无迹卡尔曼滤波的姿态解算方法,主要针对惯性器件系统误差、环境干扰大和陀螺漂移引起姿态发散等场景,在预处理的基础上,利用优化AUKF的高精度特性完成姿态解算。从实验结果效果看:预处理效果明显,基本消除了噪声干扰和信号野点值,通过优化AUKF的姿态解算,姿态角精度进一步提高,该方法实现简单和有较强的实用性,是一种高精度的姿态解算方法。
