基于BP神经网络模型的商品房价格预测研究

乔维德

（无锡开放大学 科研与质量控制处，江苏 无锡 214011）

0 引言

随着我国经济的快速发展和房地产市场迅猛发展，房地产行业已经逐渐成为我国国民经济的重要支柱，成为国家和地方经济发展不可或缺的组成部分.房地产业的稳健和可持续发展，对于推进经济社会发展、提高人民生活水平具有重要的作用.房地产业的飞速发展带动房价在不断上升，目前很多地区的房地产业已成为国民经济增长的引擎，商品房价格的走势也普遍受到越来越多老百姓的密切关注.但是，近年来由于房地产供需不平衡以及信息不对称等原因，导致商品房价格过快上涨或持续攀升.影响和决定商品房价格的因素错综复杂，如人均收入、国民生产总值（GDP）、居民消费水平、建筑成本、银行贷款等.如何有效地对房价走势进行科学分析和预测，从而抑制房价过高增长一直是经济社会关注的热点问题，也是关乎老百姓生活和每一个家庭的民生问题，所以对商品房价格问题的研究有助于解决经济问题和民生问题.

常用的传统房价预测方法有灰色模型、时间序列模型、多元线性回归模型等，如：丁月芝[1]提出建立时间序列模型对济南房价进行预测；王莹等[2]建立基于GM（1，1）灰色系统模型对淮安市商品房价格进行分析预测；张元姣[3]通过建立线性回归模型对上海市房价进行预测，等等.但由于房价预测呈现复杂的非线性关系，加之房价数据波动较大，经常发生无规律、随意性变化，所以采用传统房价预测方法存在着很大的局限性.于是不少学者利用具有较强非线性映射功能的BP神经网络来预测房价，如：周学君等[4，5]采用人工神经网络BP算法分析和预测房价走势；杭晓亚等[6，7]提出基于遗传算法的BP神经网络房价预测方法；张卉[8]提出基于粒子群优化BP神经网络的房价预测方案，等等.以上各种方法通过仿真分析与实验验证，都能实现对房价的预测，并取得了一定的成效.然而BP算法具有较强的非线性映射及泛化能力，但此算法计算量大、收敛速度过慢、极易陷入局部最小值；遗传算法是一种全局优化算法，但这种算法易陷入“早熟”；粒子群算法搜索速度快、效率高、算法简单，但其局部寻优能力较差，容易陷入局部最小，所以对房价的预测结果往往不准确，误测现象比较多.鉴于以上问题和不足，本研究充分利用果蝇优化算法全局搜索能力强、收敛速度快，以及蛙跳算法局部深度搜寻能力强的优势，通过果蝇算法与蛙跳算法融合形成果蝇-蛙跳算法来优化用于商品房价格预测的BP神经网络结构参数，提高未来商品房价格预测的科学性和精准度，为房地产业的可持续发展提供科学决策咨询.

1 商品房价格预测模型

商品房价格受到诸多因素的变化影响，一是购房需求的影响因素，如人均收入、GDP、居民消费水平等.居民的收入水平决定支出的能力，居民只有具备购买力，才会实现购房需求；GDP指标在一定程度上影响着人们对国家或某一地区经济发展环境的判断，很大程度上影响着投资者、投机类型消费者的购房需求.二是商品房供给的影响因素，如土地价格、建筑成本、银行贷款等.商品房的建筑成本主要取决于建材价格；商品房施工面积也影响房地产的定价和供给量；银行贷款无论对于房地产开发企业还是购房者来说，都存在较大的依赖度.根据上述分析，从购房需求、国民经济、金融、开发成本等维度分析，确定影响房地产商品房价格的关键性因素，即地区人均生产总值x1、房地产开发投资额x2、城镇居民人均住房使用面积x3、城镇居民人均可支配收入x4、城镇居民人均消费性支出x5、城镇总人口数x6、银行贷款利率（5年）x7、商品房土地交易价格x8、商品房销售面积x9、建材价格x10共10个主要影响因素.笔者采用BP神经网络建立房价的预测模型，并利用果蝇-蛙跳算法优化BP网络的结构参数，然后将训练的BP神经网络模型用于对房价的准确预测.用于房价预测的BP神经网络评价模型如图1所示.选取以上10个主要影响因素x1～x10数据预处理（即归一化）后的值作为BP神经网络的输入变量，BP神经网络的输出变量s*经过反归一化处理后的s值作为商品房平均销售价格的网络预测值.ωij代表BP神经网络对输入层和中间层之间的连接权值，Tki代表中间层与输出层之间的连接权值，中间层、输出层节点阈值分别为θi，θk，Q为BP神经网络的期望输出值[9，10]，即商品房平均销售价格的真实值.

2 果蝇-蛙跳算法优化BP神经网络

BP神经网络的房价预测输出值s与期望输出Q之间存在偏差，通过优化BP神经网络连接权值ωij，Tki及节点阈值θi，θk等结构参数，利用房价预测数据样本的反复学习训练，实现BP网络预测输出值s与期望输出值Q之间的最大误差达到规定的目标误差范围.因为BP神经网络初始化结构参数对神经网络输出的影响非常大，而BP算法本身对于神经网络初始结构参数比较敏感，加之BP算法收敛速度慢，又易陷入局部极值，因此采取果蝇-蛙跳算法来优化BP神经网络的初始结构参数.果蝇算法全局寻优能力强、收敛速度快，而蛙跳算法局部深度寻优能力强，以上两种群体智能优化算法各具优势，两者融合以后可以达到较高寻优精度和较快寻优速度.

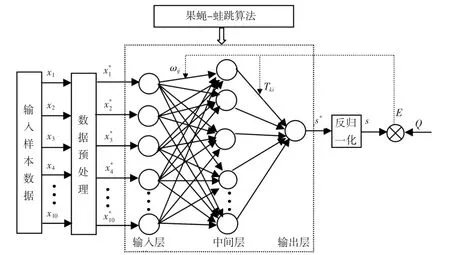
图1 房价预测的BP神经网络模型

运用果蝇-蛙跳算法优化BP神经网络结构参数的主要步骤如下[11]：

Step1，初始参数设置.设定果蝇群体数量M，果蝇算法最大迭代次数max1，果蝇群体初始随机位置坐标（X0，Y0），果蝇算法优化迭代步进值rand；蛙跳算法最大迭代次数max2，族群数m，每个族群内青蛙个体数k；

Step2，果蝇个体位置确定.果蝇个体位置坐标（Xi，Yi）根据（1）式计算确定，其中rand取值范围为[-1，1]：

Step3，果蝇个体的味道浓度计算.果蝇当前位置（Xi，Yi）与原点间距离设为hi，果蝇个体味道浓度判定值记为Gi，味道浓度适应度函数记为Fit，果蝇个体当前位置的味道浓度设为Concentration，则：

Step4，味道浓度最高的果蝇个体搜寻.

式中bestConcentration代表味道浓度最高的果蝇个体味道浓度值，其位置对应为（X，Y），此时其他果蝇个体飞向并不断靠近该位置：

Step5，果蝇算法寻优迭代判定.当迭代次数小于max1时，转入Step4；当迭代次数满足max1时，则转入Step6执行.

Step6，将由果蝇算法寻优的各个体作为蛙跳算法的初始种群，并将各青蛙个体按适应度从高到低排列.将青蛙群体分成m个族群（或子群），每个族群都分配k只青蛙.

Step7，每个族群中适应度最差青蛙个体位置更新.每个族群中适应度最好位置解记为Xb，适应度最差解位置记为Xw，所有族群中适应度最好解位置为Xg，

式中R表示 [0，1]区间上的随机数，Dj代表第j维空间移动位置距离，Dmax代表青蛙个体每次位置更新最大值. 若 Xw（new）小于 Xw，便以 Xg替代 Xb，接着按（7）、（8）式进行更新. 若更新后 Xw（new）小于 Xw，需要随机用一个新解替代原适应度最差位置解Xw.

Step8，蛙跳算法寻优迭代判定.当蛙跳算法迭代寻优次数小于max2时，转至Step7继续对族群中适应度最差青蛙个体进行更新操作；否则输出全局适应度最佳的青蛙个体，并将最优个体赋值给BP神经网络结构参数 ωij，Tki，θi，θk的最优初始值.

果蝇-蛙跳算法优化BP神经网络结构参数的流程如图2所示.将BP神经网络结构参数ωij，Tki，θi，θk视为果蝇-蛙跳算法中个体.初始化种群时随机产生一定数量的个体，作为BP神经网络的多组连接权值和节点阈值，通过果蝇-蛙跳算法搜寻最优个体位置，最优位置对应为BP神经网络最优初始连接权值和阈值.由训练样本输入BP神经网络进行学习训练，通过不断调整网络连接权值和阈值，直至网络训练的均方误差E为最小（即商品房平均销售价格的预测值与真实值之间误差最小）或满足BP神经网络设定的最大迭代次数，

式中sjk代表第j个训练样本在第k个输出节点处BP神经网络输出，Qjk代表第j个训练样本在第k个输出节点处对应的期望输出，m代表BP网络输出节点个数，n代表训练样本个数.

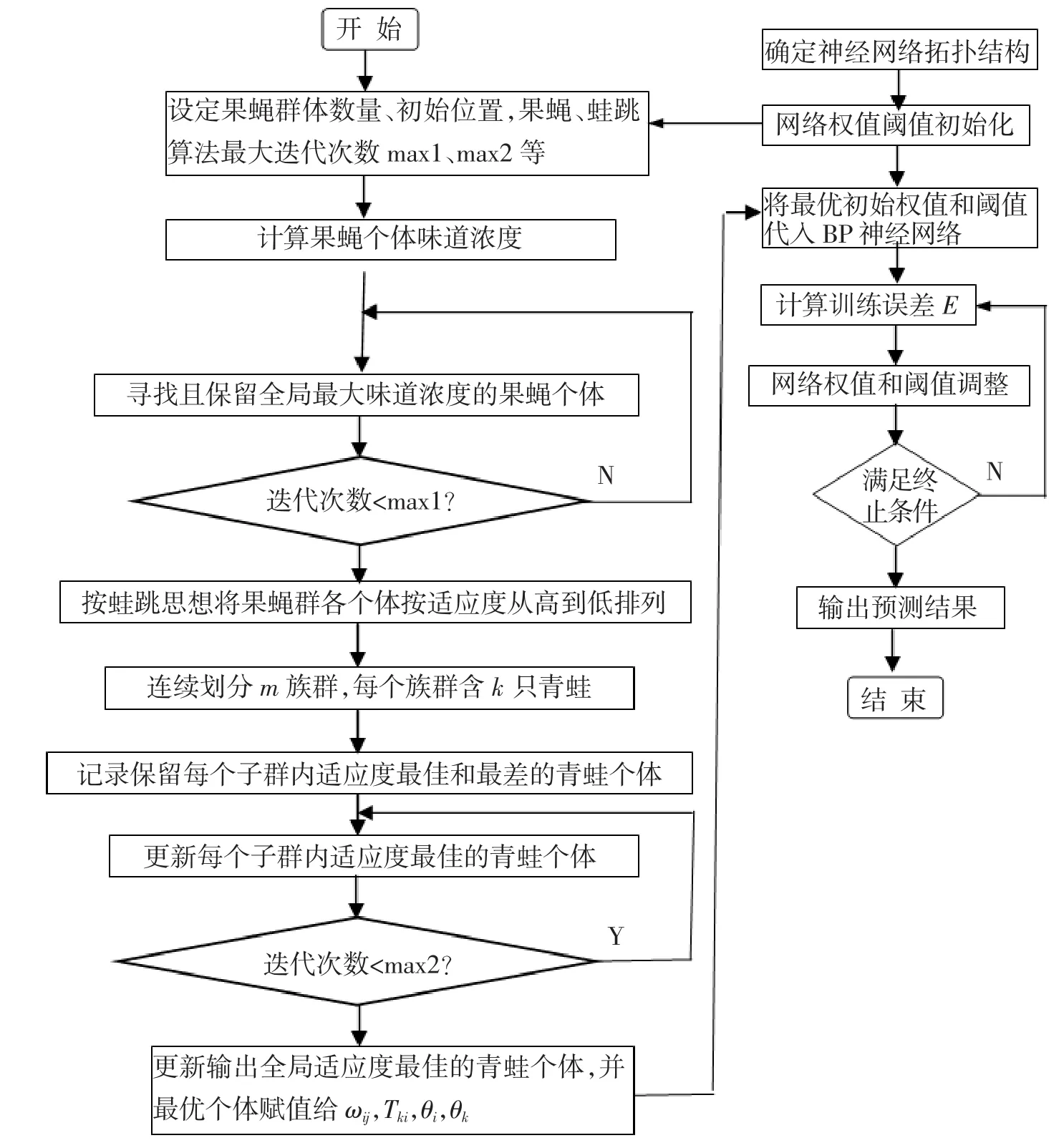
图2 果蝇-蛙跳算法优化BP神经网络流程

3 房价预测的BP神经网络模型应用

3.1 数据预处理

用于房价预测的影响因素共有10个，由于各影响因素的量纲和单位不完全相同，在利用BP神经网络预测房价时，为避免因原始样本数据过大影响网络的训练速度及其灵敏性，所以需要通过归一化数学处理，将原始有量纲的数据转换成[-1，1]无量纲的标量值，并尽可能地使数据分布均匀平滑，从而消除外界因素对神经网络预测结果的影响.本研究使用MATLAB中的premnmx函数对原始数据样本的输入和输出进行归一化处理，即：

式中x，s分别代表原始数据的输入样本和输出样本，x*，s*分别代表归一化后的数据值，xmax，xmin分别代表原始数据的最大值和最小值.在BP神经网络模型训练结束后，对于网络预测输出得到的归一化数据，需要再利用MATLAB中postmnmx反归一化函数进行处理，还原成正常的商品房平均销售价格值.

3.2 BP神经网络结构设计

用于房价预测的10个影响因素指标分别对应于BP神经网络的输入神经元，网络输入层节点数n=10.将房价预测结果s作为BP神经网络输出，输出神经元节点数m=1.BP神经网络中间层神经元节点个数h的确定，可根据Hornik公式：

计算得出中间层神经元节点个数的范围为5～21，通过反复实验测试，确定最佳的中间层神经元节点个数为12.所以，房价预测的BP神经网络拓扑结构设计为10—12—1，BP网络中间层神经元传递函数为tansig，各节点激活函数选取Sigmoid函数，输出层神经元传递函数选取purelin，其节点的激活函数选取对数S型Sigmoid函数.

3.3 训练与测试样本选取

表1列出某城市历年商品房房价及相关影响因素的原始数据.原始数据样本中含训练样本和测试样本，其中2000～2014年的15组数据用于BP神经网络的训练，2015～2018年的4组数据用于BP神经网络的测试验证；x1～x10为影响商品房价格预测的各因素原始数据值，Q为实际的商品房平均价格，用它作为BP神经网络的期望输出值.

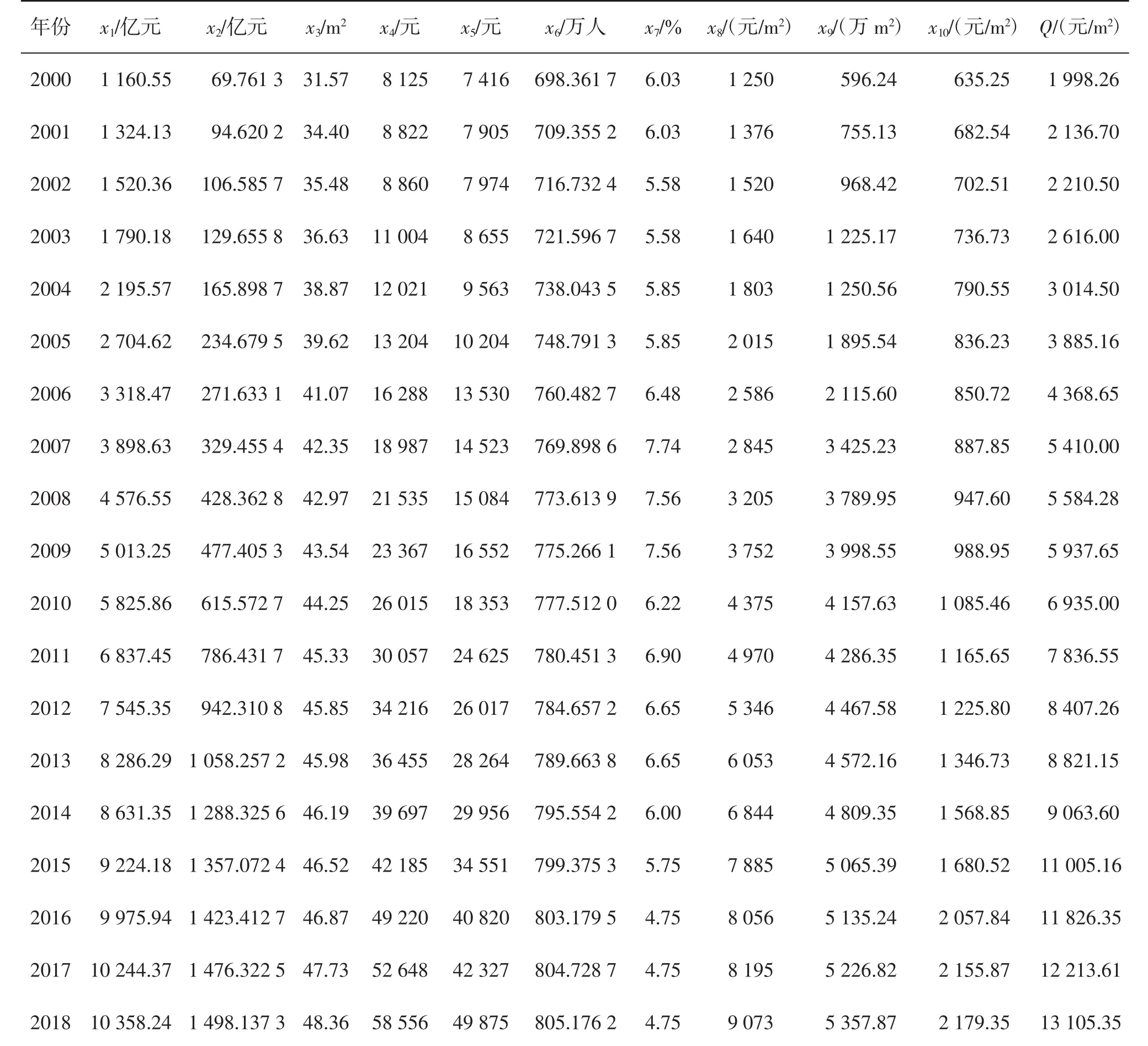
表1 用于BP神经网络训练和测试的原始数据样本

3.4 参数设置及训练、测试分析

果蝇-蛙跳算法初始化参数选取为：果蝇群体数量M＝300，果蝇算法最大迭代次数max1=200，果蝇优化迭代步进值rand=0.52；蛙跳算法最大迭代次数max2=65，族群数m=20，每个族群含个体数k=10.BP网络训练误差的目标精度为0.000 1.BP神经网络的最大迭代次数为300，目标误差为10-4.通过MATLAB软件利用表1中的2000～2014年15组数据对BP神经网络加以训练，直至BP网络达到规定的误差目标精度或最大迭代次数.网络训练误差情况如图3所示.当网络训练步数达到104步时，能满足目标误差要求，BP神经网络的训练时间短，训练精度高.2015～2018年的4组数据验证样本的测试结果如表2所示，用于商品房平均售价预测的BP神经网络输出值s与期望输出值（即商品房平均销售价格的真实值）Q之间的最大相对误差为1.79%，说明建立的BP神经网络模型能比较客观、准确、有效预测商品房平均销售价格.

为验证本研究采取的果蝇-蛙跳算法优化BP神经网络的性能，仍然使用表1中的15组训练样本和4组测试样本，先后采取BP算法、遗传算法、粒子群算法、果蝇算法、蛙跳算法、果蝇-蛙跳算法优化训练和测试BP神经网络，再进行对比分析.比较结果见表3，从表中可以看出BP神经网络经果蝇-蛙跳算法优化的网络训练速度最快、训练误差最小、预测精度最高.

图3 BP神经网络训练误差曲线

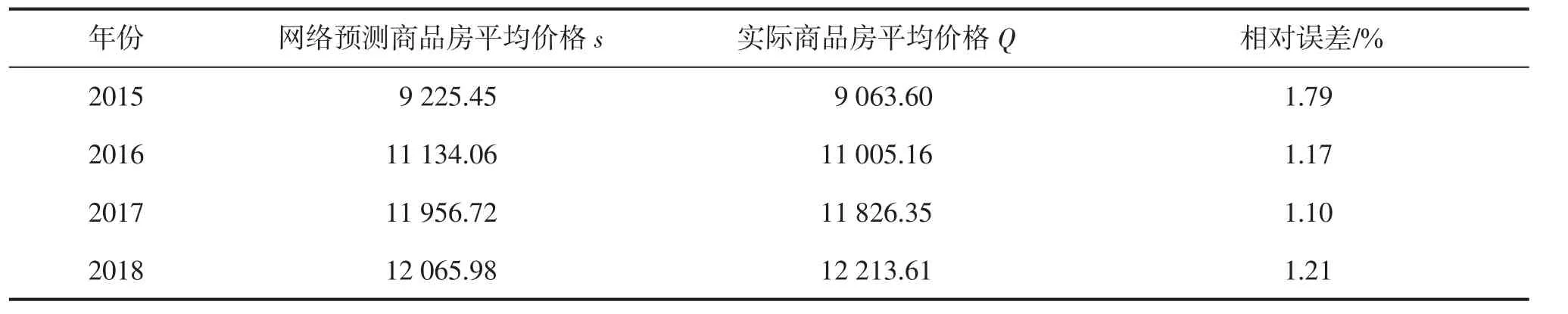
表2 网络测试样本评价结果

4 结语

选取影响商品房价格的10个主要因素作为BP神经网络的输入变量，商品房平均销售价格作为BP神经网络的输出变量，采取果蝇-蛙跳算法优化BP神经网络模型，并利用15组训练数据样本和4组测试样本对BP神经网络分别进行学习训练和测试验证，通过对商品房价格网络预测结果数据与房价真实数据的误差分析，本研究建立的用于商品房价格预测的BP神经网络模型具有较高的预测精度和可信度，对政府宏观调控房地产市场具有一定的参考价值.当然影响商品房销售价格的因素还有很多，如政府宏观调控政策、地区及城市环境、投机炒房等，从而影响BP神经网络对商品房价格预测的客观性、真实性，这些需要在以后的实际应用中不断深化研究.