振动测试系统在动力学参数测试中的应用
2019-11-26李姝佳马勋勋
李姝佳, 马勋勋
(东华大学 机械工程学院,上海 201620)
0 引 言
任何零部件都有自身的刚度和材料阻尼,获取其刚度和阻尼的方法不同,简单结构刚度,如轨道结构等可以通过理论方法得到[1];复杂机械零件,如轴承可以通过有限元等方法得到[2]。通常在机械或其他结构间都会存在零件结合(下文简称“接触系统”),形成许多结合面,结合面受到动态载荷作用,其接触面间将产生微小的法向及切向动态变形,表现为接触刚度和接触阻尼。接触问题一般分为静接触和动接触,最常见静接触刚度和接触阻尼的研究方法有经典的Herz理论[3],动接触刚度的研究方法有理论建模[4]和实验方法[5-7]。
但是,接触系统的接触刚度和接触阻尼并不是定值,有些接触系统的刚度和阻尼具有频变特性。因此,本文针对具有频变特性接触刚度和接触阻尼提出了一种通用实验测试方法,基于单自由度强迫非共振法,采用电动振动台作为简谐激励,利用加速度传感器采集信号并做数据处理,得到接触系统的等效接触刚度和等效接触阻尼。
1 振动测试方法
1.1 单自由度强迫非共振法
任何两物体的接触可以等效为两刚体接触,其结合面的接触刚度和接触阻尼通过等效弹簧刚度和等效阻尼来描述。因此,可将接触的两物体等效简化为单自由度弹簧阻尼模型,根据动力学知识,对接触物体给定已知外界激励,测试另一物体的响应,通过激励和响应分析得到接触系统的动力学参数特性,即等效接触刚度和等效接触阻尼。
等效接触阻尼在简谐强迫位移激励非共振振动的作用下,振动质量的稳态响应的频率等于激励频率,而响应的振幅和相位角与外部激励和系统本身参数有关,与初始条件无关;故本文采用简谐强迫非共振作为实验的外界激励。强迫非共振法是将简谐位移激励施加在与振动质量m不直接相连的地基上,精确测量振动物体质量m的稳态响应。通过精确分析激励与稳态响应的关系,得到接触系统动力学参数的等效接触刚度k和等效接触阻尼c(见图1)。
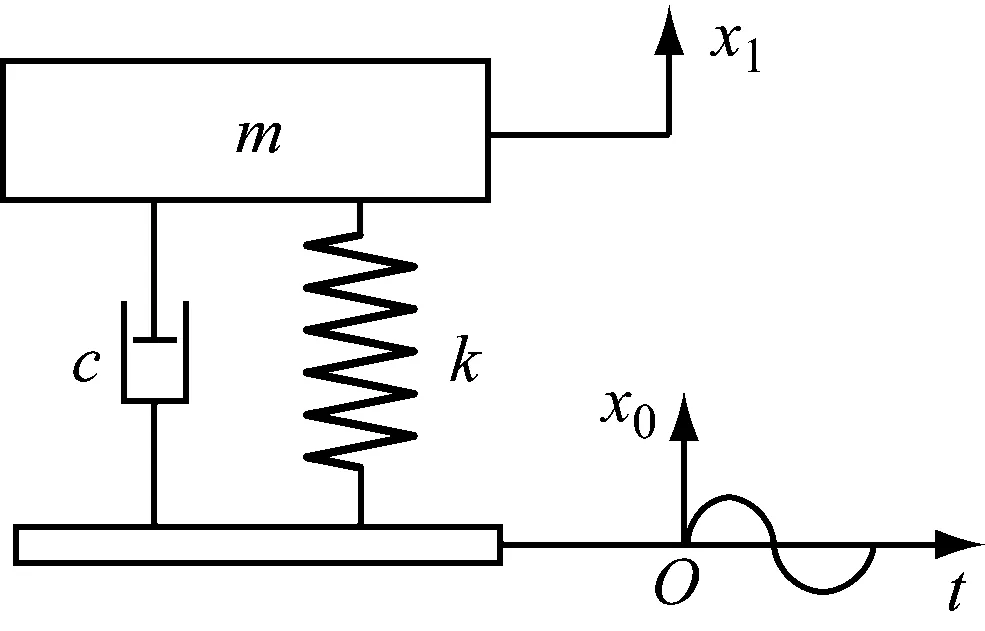
图1 单自由度等效弹簧阻尼模型
根据单自由度模型可得到测试物体在平衡位置的动力学方程:
(1)
式中:k和c分别为接触系统的等效接触刚度和等效接触阻尼;x0为简谐位移激励;x1为振动测试物体的响应。
假设简谐激励函数和响应函数分别为:
x0=a0sin(ωt+φ0)
(2)
x1=a1(ω)sin(ωt+φ0-φ1(ω))
(3)
式中:a0和a1(ω)分别为简谐位移激励和响应幅值;φ0为简谐位移激励的初始相位角;φ1(ω)为振动物体滞后于激励的相位角。
把式(2)、(3)代入式(1),方程中cosωt和sinωt前的系数分别相等,令χ(ω)=a1(ω)/a0,可得到:
(4)
(5)
1.2 电动振动系统
电动振动系统是由电动振动台台体、振动控制系统和风冷系统等组成。其中电动振动台台体的工作原理是利用恒定磁场中对台体中动圈的线圈通以电流,线圈产生直线运动;当在线圈中通以正弦交流电,则动圈产生正弦交变运动。该振动台的型号为DC-3200,台体技术参数如下:电动振动台台体型号DC-3200-36,额定正弦推力31.36 kN,最大位移51 mm,最大加速度980 m/s2,被激励部件有效质量32 kg。
电动振动系统的测试原理是先在振动控制仪的控制软件LMS Test.lab上进行对应设置,如激励幅值、采样频率等,然后通过振动控制仪发出激励正弦电信号在功率放大器进行放大,将该电流通过台体动圈中的线圈,使动圈产生设定的正弦振动激励,通过加速度传感器分别采集激励x0的信号和响应x1的信号,具体流程见图2。
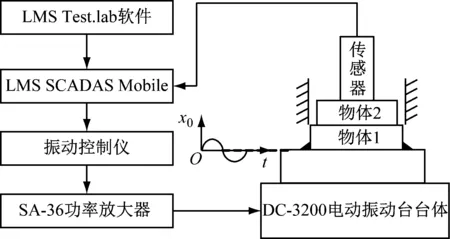
图2 电动振动系统测试控制流程
1.3 相关分析法
本实验基于单自由度强迫非共振法,可知稳态响应频率与激励频率相等。简谐激励x0与同频简谐响应x1理论上是连续的正弦函数,但在实际信号采集和处理过程中,只能用很小时间间隔的离散点(采样频率)来描述x0与x1分别与时间t的关系。在后续描述中将x0与x1统称为信号。由于信号频率都为激振频率f,所以需要采集信号的频率fc满足信号处理的采样定理,即fc≥2f。
同频简谐振动相位差的测量方法也有多种,如线性扫描法、椭圆法和频谱分析法等。本文利用互谱或相关分析获得x0与x1之间的相位差。
本文采集到的信号为离散信号用x(n)表示,离散信号的自相关函数为:
(6)
式中:N为周期采样点个数,且N=fc/f;τ为时间间隔;t为时间变量。
周期离散信号x(n)和y(n)的互相关函数为
(7)
把式(2)、(3)代入式(6),令τ=0,可得到:
(8)
把式(2)、(3)代入式(7),令τ=0,可得到:
(9)
由此可知,当τ=0时可通过式(6)得到Rx0x0(0)和Rx1x1(0)的值;当τ=0时可通过式(7)得到Rx0x1(0)的值。再结合式(8)和式(9)可计算得到a0、a1(ω)和φ1(ω),把该结果代入式(4)和式(5)可求得接触系统的等效接触刚度k(ω)和等效接触阻尼c(ω)。
2 算 例
2.1 橡胶圈刚度和阻尼实验测试
橡胶是具有可逆形变的高弹性聚合材料,橡胶业的发展起源于汽车工业,由于橡胶具有高弹性、黏弹性、缓冲减振特性,现已在各行各业中得到广泛应用[8]。橡胶在宽广的频域范围内具有较好的减振效果,而且橡胶产品的刚度和阻尼具有频变特性,橡胶圈在柔性支撑系统如纺丝卷绕机锭轴中起到了重要作用。橡胶圈在受到外界载荷时,表现出强非线性特性,其接触刚度和接触阻尼具有频变特性[9],理论计算建模求解非常困难。本文通过实验方法测试某型号卷绕机锭轴中橡胶圈的动力学参数,其中卷绕机锭轴的卷绕速度为3 000~8 000 r/min,对应工作频率为50~150 Hz,测试相关参数如下:橡胶圈规格(线径×内径)3.5 mm×44 mm,加速度传感器型号2106C,振动质量m=4.5 kg,振动台位移激励幅值0.05 mm,激励频率范围50~400 Hz。
实验测试系统如图3所示。橡胶圈作为柔性支撑中的重要组成部分,橡胶圈的试验测试模型是根据橡胶圈在柔性支撑中的安装位置和尺寸来设计,测试时柔性支撑中橡胶圈的个数nT=4,6,如图3(a)所示;其中振动块质量是根据本实验振动频率最高为400 Hz时,保证支撑座与振动块不发生碰撞进行设计的。实验时台体动圈进行正弦激励,利用压电式加速度传感器采集控制信号(见图3(b)传感器1)和相应信号(传感器2)。
把采集到的加速度信号利用1.3节的相关分析法得到a0、a1(ω)和φ1(ω),然后代入式(4)、(5)得到橡胶圈支撑系统的等效支撑刚度和等效支撑阻尼,计算结果如图4所示。
由图4可知,橡胶圈的接触刚度和阻尼具有频变特性,刚度和阻尼在频率范围内有很大的变化,由文献[10-12]可知本实验测试方法的正确性。因此,橡胶圈的实验测试方法为柔性支撑/转子动力学研究提供动力学参数。
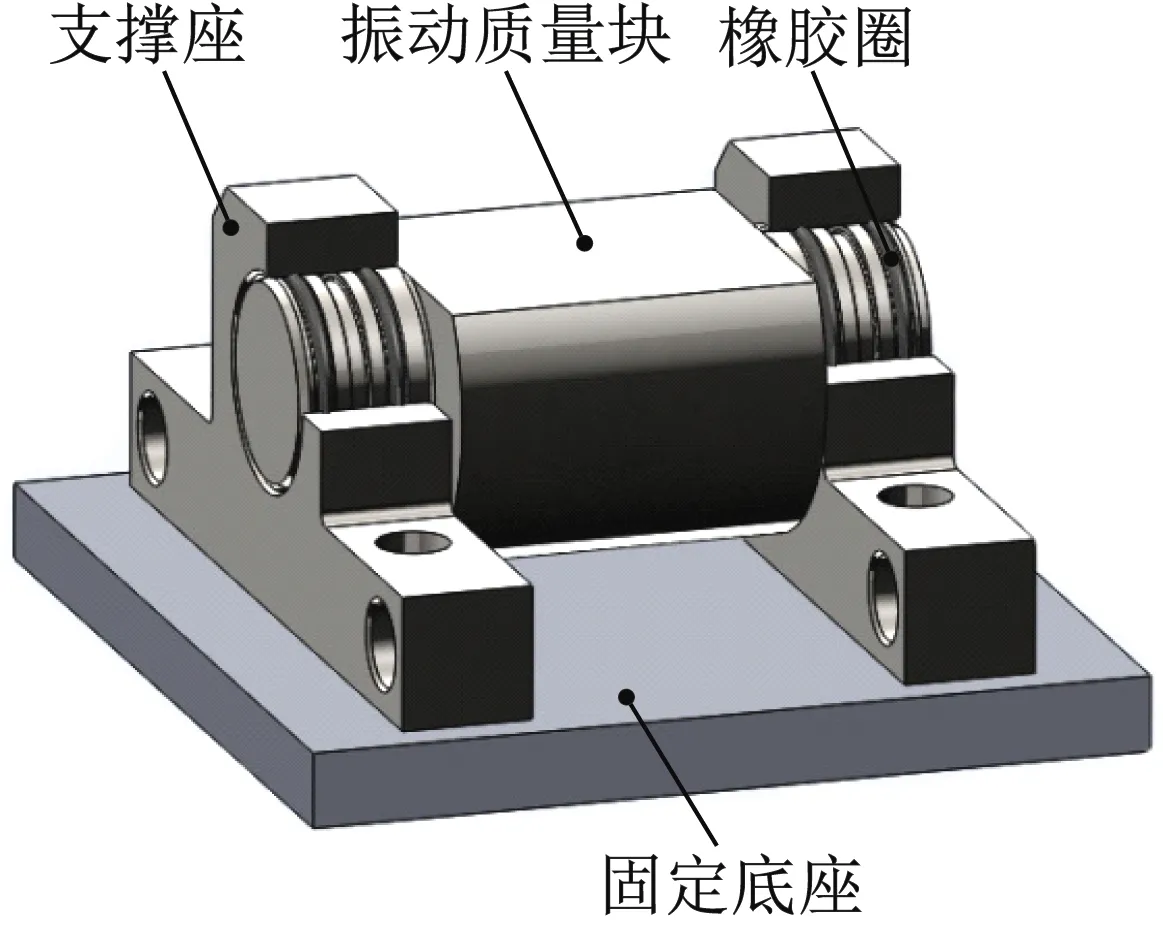
(a) 橡胶圈实验测试模型

(b) 实验测试系统
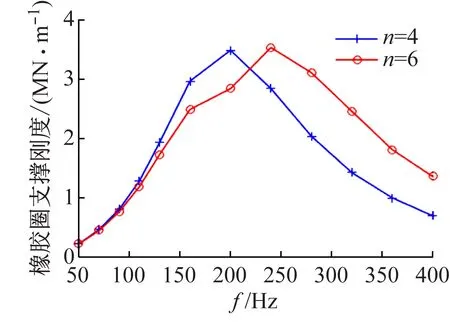
(a) 橡胶圈支撑刚度
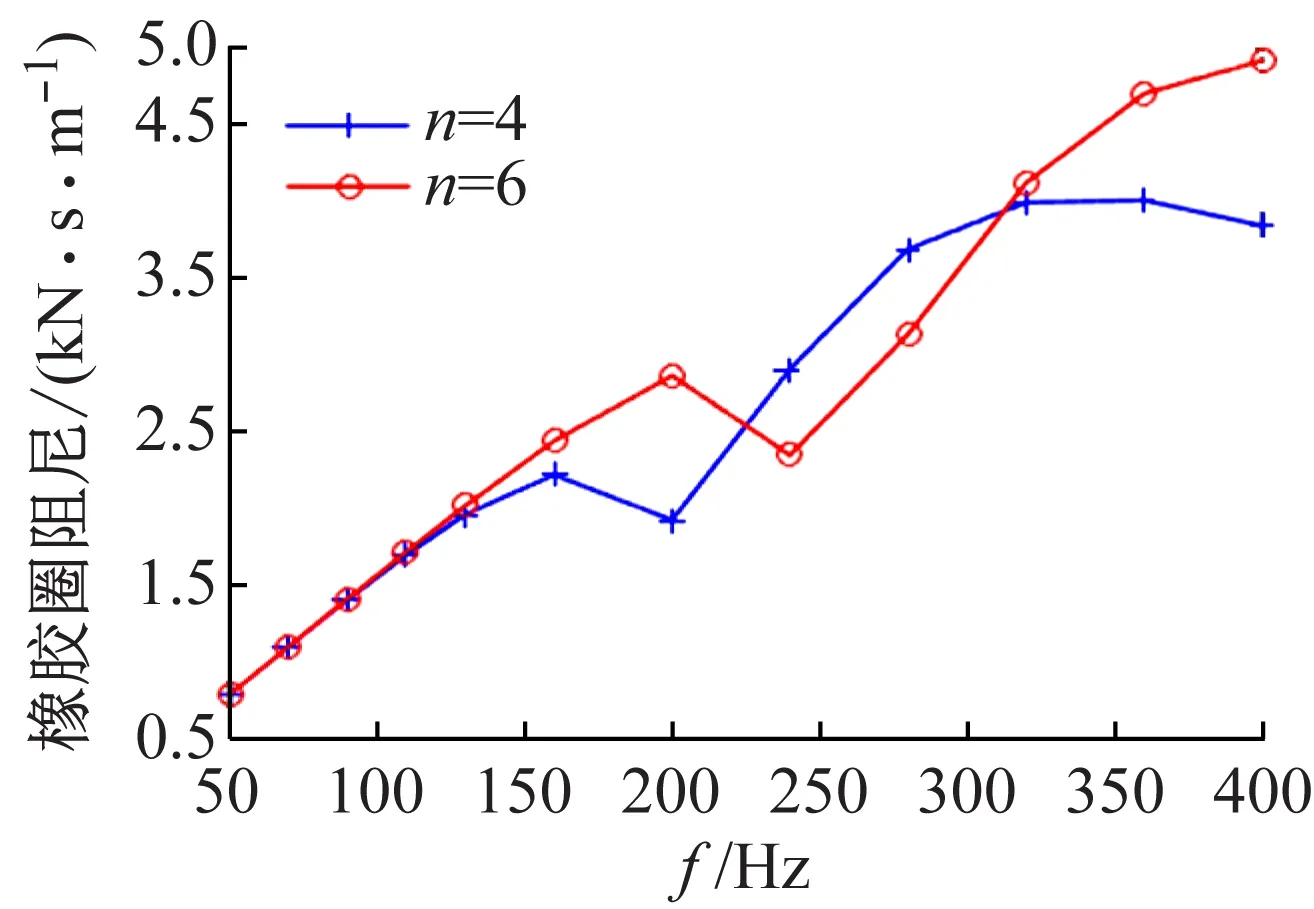
(b) 橡胶圈阻尼
2.2 “锭轴-卷装-接触辊”系统等效接触刚度和等效接触阻尼测试
卷装为涤纶长丝和纺织成品的中间产品,为了方便后续的加弹、储存、运输等需要,长丝通过卷绕机卷绕成圆盘形状,又称丝饼。卷装既要求卷绕密度大,又要求外观形状符合规定且不塌边、无污染,同时便于在后续工序退绕。某型号卷绕机的卷绕线速度为3 km/min,涤纶长丝生产时其线速度恒定,随着卷装直径的增大锭轴卷绕角速度从8 000 r/min降低到3 000 r/min。因此,锭轴、卷装和接触辊形成转速频变、质量时变的复杂系统,且接触辊对卷装表面具有一定压力,通常为9~18 N,该系统的等效接触刚度和等效接触阻尼对卷装质量和卷绕机性能都有非常重要的影响[13]。本文对“锭轴-卷装-接触辊”系统的接触特性进行试验研究,测试所需卷装的参数如下:线密度220 dtex/72,测试卷装直径258 mm,加速度传感器型号2106C,激励位移幅值0.05 mm,振动接触辊等效质量12.36 kg。
为了能够用实验的方法测试得到“锭轴-卷装-接触辊”系统的接触刚度和接触阻尼,本文设计了对应实验测试装置,其中该装置的锭轴与接触辊与某型号卷绕机一致,如图5所示。当卷装直径为258 mm时对应锭轴转速为4 690 r/min,确定振动台激励频率78 Hz;根据对卷绕机锭轴工作时测得振动幅值为0.05 mm,确定位移激励幅值。

图5 “锭轴-卷装-接触辊”模型及实验测试
根据纺丝工艺确定相关测试参数后,确定所用实验设备全部正常后进行“锭轴-卷装-接触辊”系统的动力学参数测试,实验测试时保证测量卷装直径不变,改变接触辊对卷装的接触压力,得到结果通过数据处理得到“锭轴-卷装-接触辊”系统的接触刚度和接触阻尼,计算结果如图6所示。

(a) “锭轴-卷装-接触辊”系统接触刚度
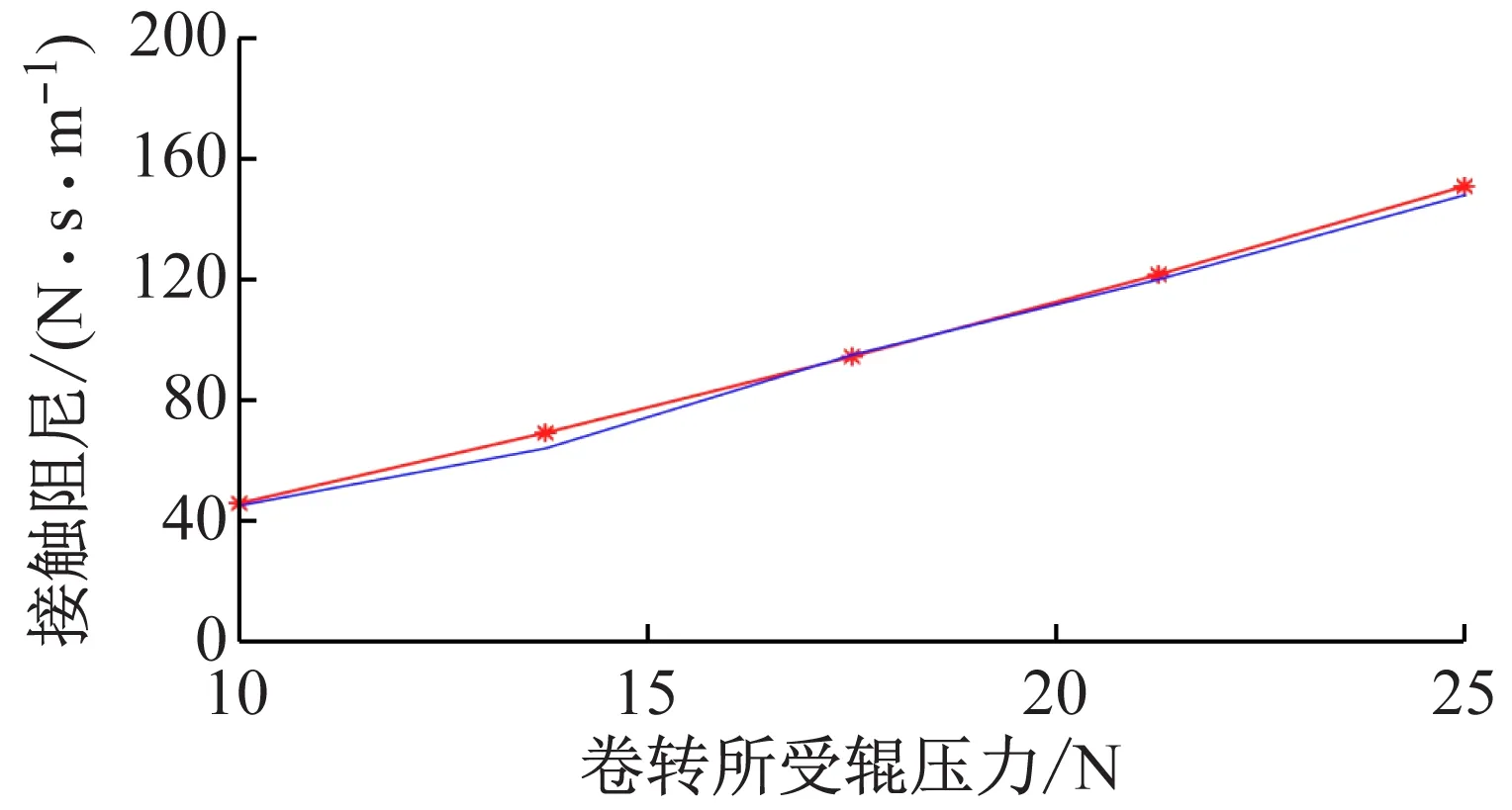
(b) “锭轴-卷装-接触辊”系统接触阻尼
由实验可知,“锭轴-卷装-接触辊”系统的接触刚度和接触阻尼都随卷装所受接触辊压力的增大而增大。但是若设定工艺的接触压力过大则会导致卷装塌边等情况。因此,“锭轴-卷装-接触辊”系统动力学参数测试实验能够为纺丝工艺研究提供参数和理论指导。
3 结 语
本文基于单自由度强迫非共振法,采用电动振动系统进行激励以橡胶圈和“锭轴-卷装-接触辊”系统为对象研究了动力学参数,快速、准确地得到了刚度和阻尼。本文提出的这种动力学参数测试的方法具有通用性,只需设计对应的夹具或满足测试工艺的装置就可以快速有效得到相关动力学参数,如新型复合材料等。
