一个布利安香点特殊情形在解题中的应用

李伟健

(安徽省滁州中学 239000)

布利安香点，是著名数学家布利安香在1806年发现的一条重要结论.它是帕斯卡线的对偶命题，布利安香点的发现时间晚于帕斯卡线的发现时间(1639年).

这一结论在解决共点问题中有着十分广泛的应用，本文探讨的是应用布利安香点解决与之相关的若干问题，并且揭示问题的本质特征.同时，在解决问题的过程中给出高师院校教材《高等几何》(朱德祥，朱维宗著)若干修订建议.

布利安香点对于任意一个外切于一条二次曲线的六边形，它的三双对顶的连线共点，即布利安香点.

当布利安香定理中的三对相邻的元素重合时，那么可以得到下面的命题，即：一个三角形外切于一条二次曲线，那么其三顶点与对边上切点的三条连线共点.下面介绍布利安香点的这一特殊情形在解题中的应用.

张正义老师在文[1]中探讨了一道高中数学联赛试题，并且提出了抛物线和椭圆中的类似命题.观察这一道竞赛试题，即：

命题1如图1，锐角△ABC内接于圆O，过圆心O且垂直于半径OA的直线分别交AB，AC于点E，F，设圆O在B，C两点处的切线相交于点P，求证：直线AP平分线段EF(选自2012年全国高中数学联赛陕西省预赛第二试的第三题).

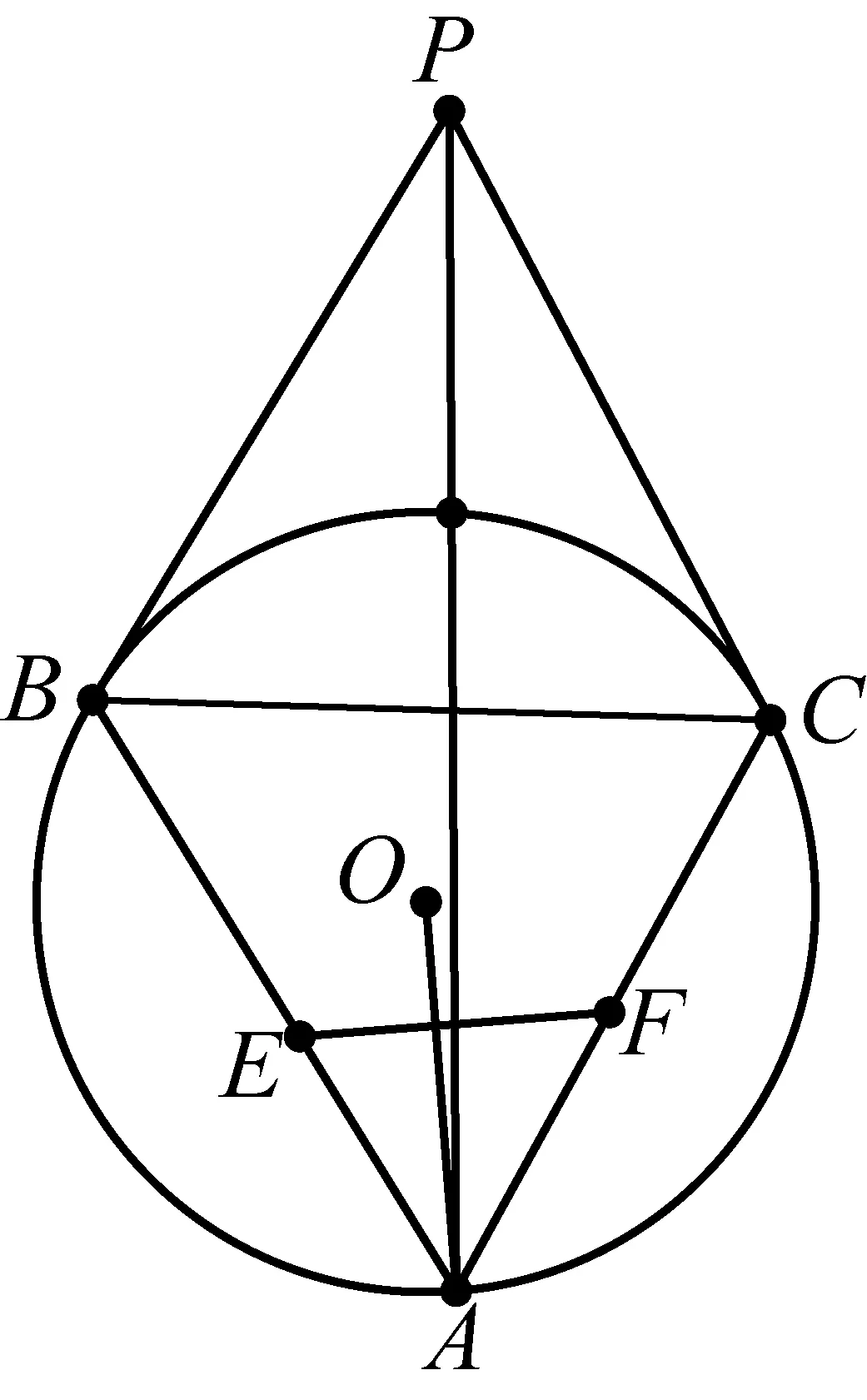
图1

事实上，命题1的结构特征可以应用布利安香点予以很好的揭示，下面给出一个简要证明，即：

证明如图2，设B，C两点处的切线分别交点A处的切线于点M，N，那么AP、BN、CM必交于一点(布利安香点)，AP与EF交于点G；

根据完全四边形MBCN的调和性，可知A(PM，BC)=-1，又因为直线EF与直线MN交于无穷远点(记为G)，所以(EF，GG)=-1，由此可知G是EF的中点，即直线AP平分线段EF.

图2

通过上面的证明可以发现，直线AP平分线段EF当且仅当直线EF与直线MN平行.所以命题1可以推广为如下命题，即：

命题2已知△ABC内接于圆锥曲线Γ，直线l交AB，AC于点E，F，曲线Γ在B，C两点处的切线相交于点P，那么直线AP平分线段EF当且仅当直线l与曲线Γ在点A处的切线平行.

在命题2的基础之上考察张老师提出的在抛物线和椭圆情形中的命题3和命题4，可以清晰地看到二者能够成立的根本原因.

命题3△AOB内接于抛物线y2=2px(p>0)，焦点F在△AOB的内部，过焦点F且垂直于x轴的直线分别交OA，OB于点E，F，设抛物线在B，C两点处的切线相交于点P，则直线PO平分线段EF.

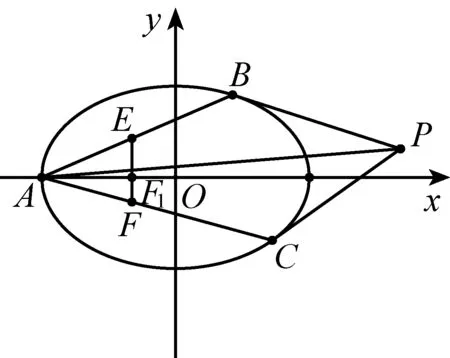
图3

命题3和命题4之所以能够成立根本原因是直线l与曲线Γ在点A处的切线平行.仔细观察命题1的证明过程中得出的结论A(PM，BC)=-1，不由得联想到朱德祥先生在其著作《高等几何》中提出的一个命题，即：

命题5如图4，设△ABC内切圆切三边BC、CA、AB于点D、E、F，那么D(CA，EF)=-1.

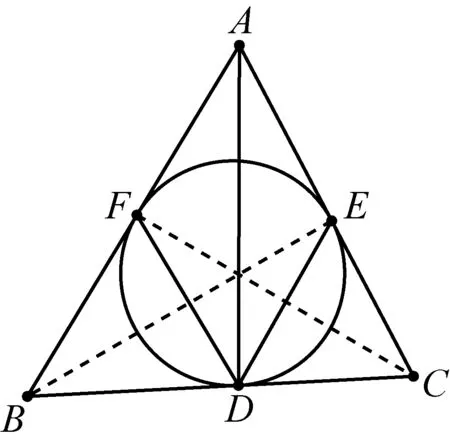
图4

朱德祥先生在处理这一问题时，应用圆的性质证实了这一命题，并且在论证之后，朱先生指出：“通过仿射变换，圆变为椭圆(如图5)，三角形ABC变为三角形A′B′C′，由仿射变换保持同素性和结合性知，三角形A′B′C′依旧外切于椭圆，又交比是简比的比，因而在仿射变换下不变，因此亦有D′(C′A′，E′F′)=-1”.如果应用布利安香点可以对这一命题得到更为透彻的解释，作为建议，或许这可能是《高等几何》以后修订可以考虑的.

图5

当前，朱先生的《高等几何》是国内为数不多的介绍射影几何，并且在高师院校影响较大的一本教材，继续考察这本教材中另一个命题，即：

命题6双曲线的任意一条切线介于两渐近线间的部分，被切点平分.转换为符号语言如下：设M为双曲线Γ上一点，曲线Γ在点M处的切线交两条渐近线于点A、B，那么|MA|=|MB|.

这一命题因其结构简单深刻，朱先生在文[2]中从双曲线共轭直径的角度解释了这一命题，下面用布利安香点给出另外一个解释，至于这一解释是否是本质的或者是稍微接近本质的，留待读者判断，即：

证明如图6，将这一命题放入射影空间，两条渐近线与双曲线Γ相切于无穷远点C、D，那么无穷远直线CD与直线AB交于点N，又AC,BD,OM交于一点，于是根据完全四点形ADCB的调和性，有(AB，MN)=-1，所以M是AB中点.

图6

这一解释也是对《高等几何》以后修订的另外一个建议.

上述讨论的主要内容是布利安香点所生成的调和点列和调和线束，这一内容在解题中的应用价值是不言而喻的.接下来，考察姜坤崇老师在文[3]提出的引理2和在文[4]提出的例6、7，调整叙述如下：

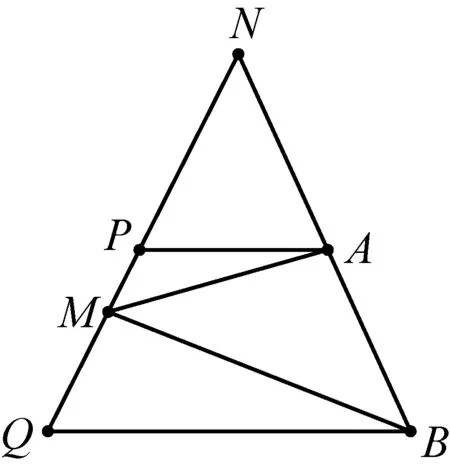
图7

这一命题可以从交比的运算性质给出一个相对来说比较简洁的论证，本文略去这一证明.

图8

姜坤崇老师对命题8从解析几何的角度分为椭圆和双曲线两种情形分别进行了论证，论证过程稍显繁琐，与结论的简洁稍显不和谐.事实上，从布利安香点的角度可以给出一个极富美感的解释，即：

证明如图9，设AP×BQ=H、AB×PQ=N，因为直线AB经过无穷远直线l的极点O，所以无穷远直线l经过直线AB的极点H，即H∈l，那么直线AP与直线BQ互相平行(欧几里得平面)；

图9

再次考察袁安全老师提出的一个命题.为此，需要王建荣老师提出的另一命题作为讨论依据，即：

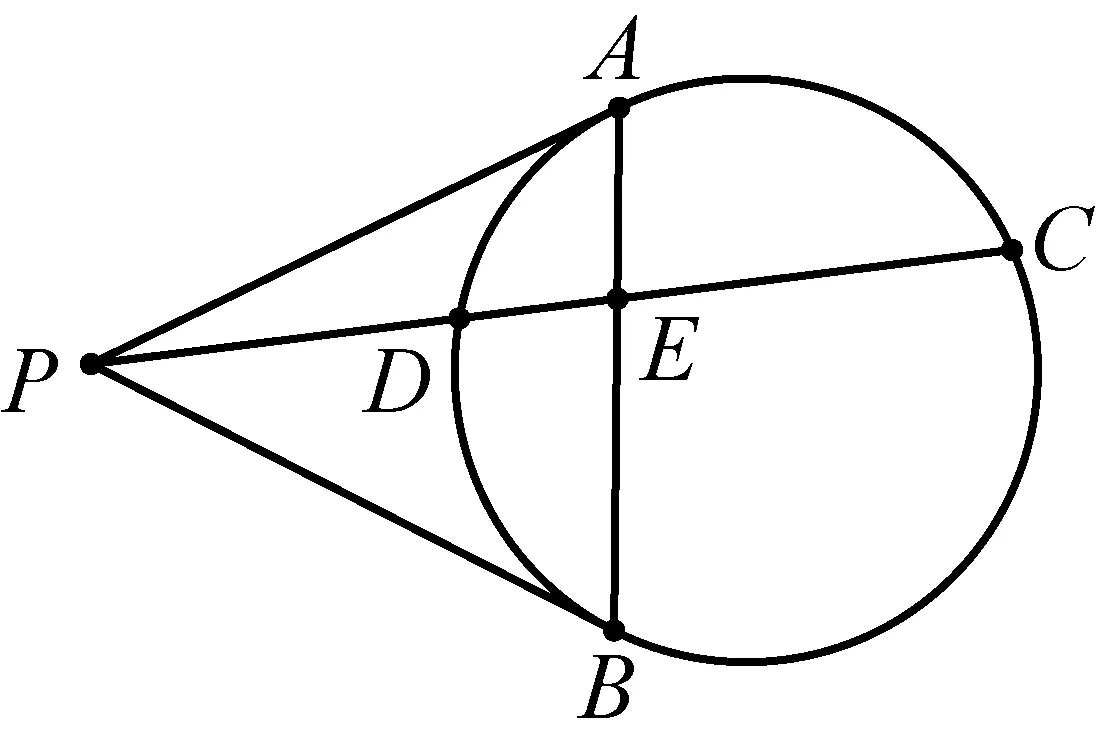
图10

实际上，王建荣老师提出的这一命题，本质是调和点列的性质，下面从交比的角度予以解释，即：

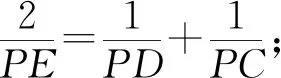
建立在命题9的基础之上，就可以应用布利安香点对袁安全老师提出的如下命题给出一个更为透彻的说明，即：

图11

证明因为△ABC的三条边与圆相切于点D、E、F，所以直线AD、BE、CF交于一点(布利安香点)，根据完全四点形ABDE的调和性，结合命题9，可得如下结论：

又因为|FB|=|DB|，

图12

经过上述讨论，读者可能对布利安香点在解题中的应用已经有所体会，布利安香点给出的解释有益于发掘问题的结构特征.下面再次考察先后由多位老师探究的一个问题，即圆锥曲线外切三角形和切点三角形之间的关系.蔡玉书和王波两位老师文[5]探讨的实际上就是布利安香点，即：

命题11若△A1A2A3的三边A1A2，A2A3，A3A1(或其延长线)与圆锥曲线Γ分别切于T1，T2，T3，则A1T2，A2T3，A3T1三线共点.

高凯老师在文[6]中提出的命题，本质上讨论的也是布利安香点，仔细观察高凯老师提出的命题，即：

命题12△B1B2B3为圆锥曲线Γ的外切三角形，△A1A2A3是相应的切点三角形，A1、A2、A3分有向线段B1B2、B2B3、B3B1的比为μ1、μ2、μ3，那么μ1·μ2·μ3=-1.

读者可能已经觉察出，这一定理的结构特征是由布利安香点生成的共点结论的塞瓦定理表述.苗相军和孙胜田两位老师在文[7]中提出的另外一个问题是本文着重讨论的对象，即：

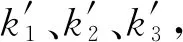
图13

实际上，苗相军和孙胜田两位老师提出的命题13的结构特征和笔者对高凯老师提出的命题12结构特征的判断是一致的，为了详细解释笔者的这一判断，需要审视塞瓦定理中所蕴含的线束斜率之间的关系.

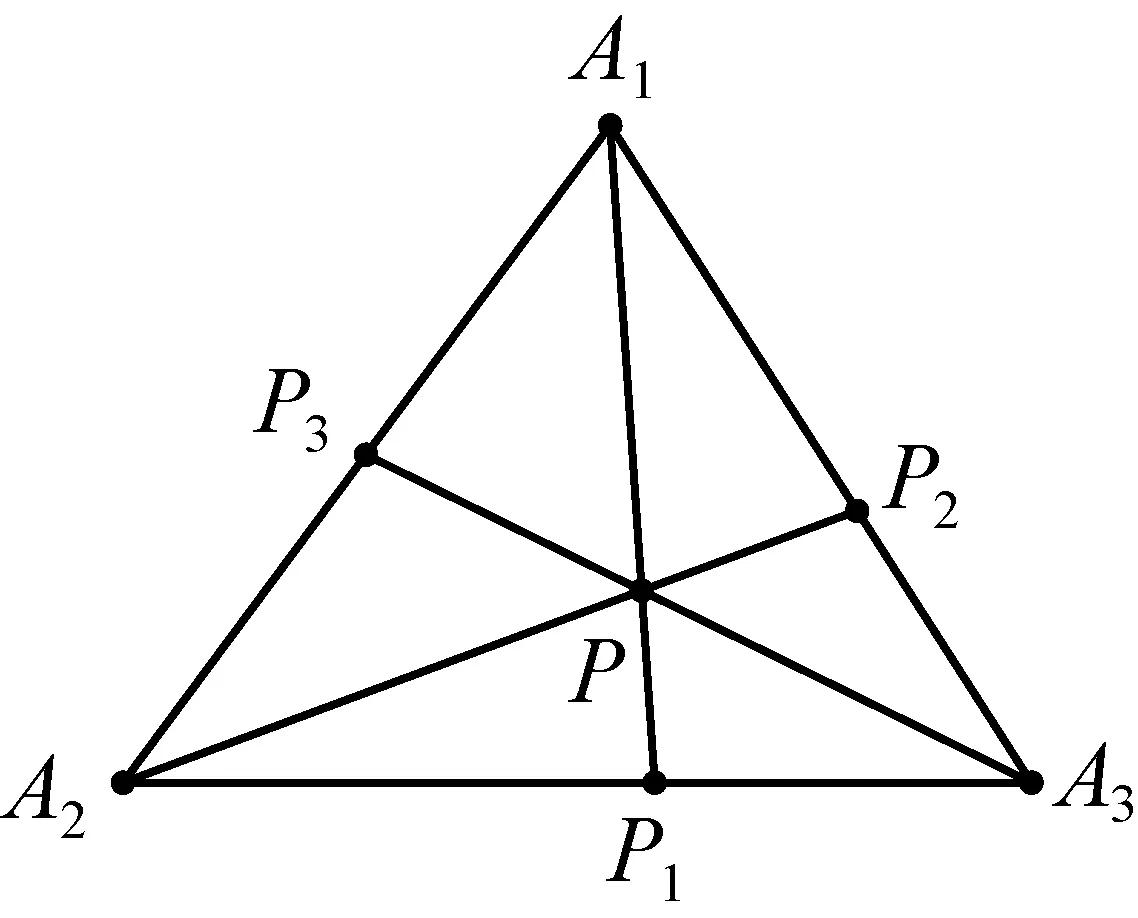
图14

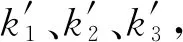
理由如下：① 设直线A1A2，A2A3，A3A1上的无穷远点为L，M，N，所以可以得到如下结论

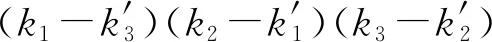
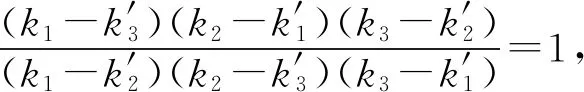
同理可得②式成立；

③根据完全四边形的调和性，

可得P1(A1P1，P2P3)=-1，

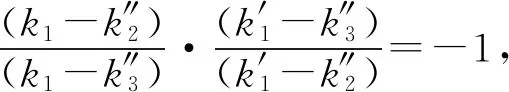
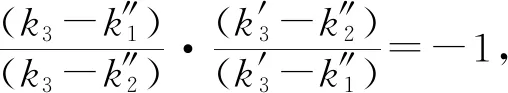
以上三个等式结合②可推出③成立.应用③可以解释命题13.

通过对塞瓦定理中线束的斜率关系的讨论，读者至此已经可以看到苗相军和孙胜田两位老师提出的命题13的结构特征的确是布利安香点生成的共点结论的塞瓦定理表述.