基于参数优化的非饱和尾矿砂渗流场解析解研究

林雪松， 王 东， 王来贵， 王永吉， 李俊岑

(1.辽宁工程技术大学 理学院，辽宁 阜新 123000; 2.阜新高等专科学校 工程系，辽宁 阜新 123000; 3.辽宁工程技术大学 力学与工程学院， 辽宁 阜新 123000)

1 研究背景

作为具有重大安全隐患的人造泥石流危险源，尾矿坝一旦发生溃决将对下游人民的生命财产和生存环境造成重大破坏[1-3]，因此，一直以来都是研究的重点。近年来，由于尾矿颗粒越来越细[4-5]，固结越来越困难，形成坝体溃决的概率呈不断上升的趋势[6]，该趋势使尾矿坝安全问题引起许多学者的关注。水的分布状态是影响尾矿坝安全的重要因素，尾矿坝中有相当一部分水分是存在于非饱和尾矿砂中的，在坝体的安全状态评估中，非饱和部分内部水分分布的影响必须予以考虑[7]，因此针对该部分水分分布的计算研究便具有重大意义。多年来国内外学者针对非饱和渗流计算问题进行过很多有意义的研究。Neuman[8]首先提出通过有限元方法解决二维饱和-非饱和渗流问题，彭华等[9]对渗流问题的有限元分析方法加以改进，提出了修正容水度和加速迭代收敛技术的新方法，消除了非饱和渗流计算中存在的数值弥散现象，提高了收敛速度。王铁行[10]考虑含水率和密度影响，给出了非饱和黄土路基水分场的数值计算模型，并探讨和确定了模型参数。刘杰等[11]研究了非饱和土路基毛细作用的数值与解析方法。李毅等[12]运用变单元渗透系数法，对FLAC3D软件进行二次开发，准确得出了连续光滑的自由水面，求解出了饱和-非饱和渗流场。刘豪杰等[13]通过自己建立的某深厚覆盖层土石坝三维渗流有限元数值模型计算，进行了针对该土石坝渗流控制方案的合理优化。刘梦茹等[14]运用非饱和渗流理论得到了包气带一维液相运动方程解析解。

纵观以往的研究，非饱和渗流计算的研究重点均在数值计算方法方面，解析方法研究的较少，即便使用解析方法也仅限于处理一维问题。数值方法的实际工程意义是有目共睹的，但重视数值方法的同时也不应该完全忽视解析方法，同时还应重视解析法与其他方法的结合。

本文拟从非饱和渗流的Richards方程出发，得到二维非饱和尾矿砂稳态渗流含水率的解析解，然后利用已有试验数据，通过参数优化的方法计算解析解中引入的待定系数，从而使解析解完整，最后对含水率计算值与实测值进行对比，以此考察解析解的实际应用效果。本文的主要目的是通过研究得出非饱和尾矿砂内的水分分布规律以及含水率计算的思路与方法，为考虑非饱和部分的尾矿坝安全评估工作提供基础资料。

2 解析模型的建立

Richards方程是解决非饱和渗流问题的基本工具，若以体积含水率θ为求解的主要参量，坐标系z轴以竖直向上为正，则三维问题中的Richards方程的形式如公式(1)所示。

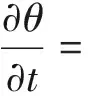
(1)

式中：θ为体积含水率，mm3/mm3；D(θ)为非饱和尾矿砂中水的扩散系数，mm2/s；K(θ)为非饱和尾矿砂的导水率， mm/s。

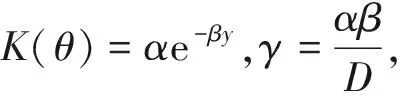
(2)

θ|x=0=A1e-A2yθ|x=q=A3e-A4y

(3)

θ|y=0=A5e-A6xθ|y=h=A7e-A8x

(4)

式中：α、β和A1～A8均为引入的无量纲待定系数，在应用模型之前，需要先将所有参数的取值确定；q为求解区域x方向的最大坐标值，mm；h为求解区域y方向的最大坐标值，mm。

3 解析模型的求解

3.1 解析解的得出

令θ=w+v，v=Ax+B，w、v、A、B均为任意函数，假设v满足边界条件公式(3)，将v代入边界条件公式(3)解得：

(5)

将θ=w+v代入方程和边界条件公式(2)～(4)得到关于w的方程和边界条件如公式(6)～(10)所示。

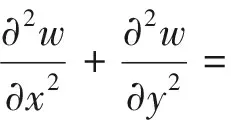
(6)

w|x=0=0

(7)

w|x=q=0

(8)

(9)

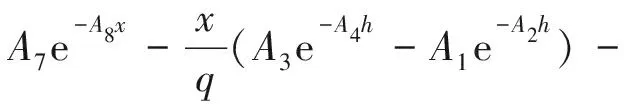
A1e-A2h

(10)

利用分离变量和傅立叶级数法可得到w，然后得到含水率空间θ分布的表达式为：

(11)

公式(11)中Cn、Dn的形式为：

(12)

(13)

很明显最终的结果具有无穷级数的形式，但因系数均具有很强的收敛性，所以在实际应用当中只取其中前几项即可。

3.2 模型参数的计算

3.1节中虽得出了解析解的具体形式，但其中涉及共计11个待定系数，在使用模型之前必须得到所有待定系数的值，否则模型是不完整的。因此，在结合试验数据的基础上进行参数优化不失为一种简单高效的方法。参数优化的方法很多，通过多方对比，最终决定采用混沌粒子群优化算法(Chaotic Particle Swarm Optimization, CPSO)。

3.2.1 运算的基本原理 算法的基本公式为：

vij(t+1)=ωvij(t)+c1r1j(t)(pij(t)-xij(t))+

c2r2j(t)(pgj(t)-xij(t))

(14)

xij(t+1)=xij(t)+vij(t+1)

(15)

zn+1=μzn(1-zn) (n=0,1,2,…)

(16)

式中：下标“i”为粒子的序数，本文取80个粒子；下标“j”为未知参量序数，如前述共有11个未知参数；t为迭代次数，本文在参考试算经验的基础上将迭代总次数取为1 000；c1、c2为两个加速常数，取值为c1=c2=1.70，c1与c2之间必须无任何关联；r1j(t)和r2j(t)为两个在0～1之间取值的随机数，每次迭代中均由计算机重新给出；ω为速度的惯性权数，取为1；vij(t+1)和xij(t+1)分别为t+1次迭代的速度和位置；vij(t)和xij(t)分别为t次迭代的速度和位置；pij(t)和pgj(t)分别为t次迭代的局部最优和整体最优。公式(16)为Logistic系统迭代公式，当初值z0满足0≤z0≤1时，通过(16)式可形成一个混沌集合，使系统完全处于混沌状态，避免计算陷入局部最优。公式(16)中μ为控制参量，取值为4。以上各参量均无量纲。

3.2.2 运算的基本过程 首先在位置、速度的取值范围内随机给出二者的初值，将c1、c2、ω和最大迭代次数等参数赋值，然后进入循环。每个循环中的运算步骤与内容如下：

(1)由公式(11)计算和对比分别得到局部最优和整体最优。

(2)将整体最优从原解空间映射到[0,1]范围内，然后作为初值通过公式(16)迭代29次得到一组混沌向量，再将该组向量映射回原解空间，从中计算出最优值，随机替代当前粒子群中任意一个粒子。

(3)按公式(14)和(15)更新速度和位置，并替换速度和位置中超出取值范围的数值，从第(1)步开始进行新的计算，直到达到最大迭代次数。

4 模型的有效性验证

4.1 已有试验结果及模型拟合效果

为计算模型参数和验证模型的适用性，笔者进行了尾矿砂非饱和渗流试验，获得了非饱和尾矿砂稳态含水率的分布结果与特点。试验采用的尾矿物料粒径很小，完全可称为细尾矿砂[15-16]。试验装置正面及非饱和渗流稳定后状态如图1所示，装置主体部分为蓄水池(100 mm×100 mm×1 000 mm)和尾矿物料池(1 000 mm×100 mm×1 000 mm)。蓄水池的作用是为尾矿物料的非饱和渗流提供水头恒定的水源，试验中保持水头高度50 mm不变。尾矿物料池用于盛装干尾矿物料，物料池正面面板上设置的网格点是用来标记需测量含水率的位置的，在水平和竖直方向上，格点间距均为100 mm。图1中AA′表示稳定后的润锋，BB′表示实验中尾矿砂试件内出现的一个裂缝。从图1中可看出AA′清晰的将试验尾矿物料分为干尾矿砂和湿尾矿砂。图1中矩形区域OCFE是一个位于湿尾矿砂内部的矩形，可用来作为一个求解域，在矩形域上分别建立了x轴和y轴，矩形域内共计包含了50个数据点，可用来拟合参数。矩形域长900 mm，宽400 mm，则前述公式(11)中q=900 mm，h=400 mm。测量得到的竖直向含水率分布曲线如图2所示，水平向含水率分布曲线如图3所示，由图(2)～(3)可知，无论在竖直还是在水平方向，含水率均逐渐降低，降低的趋势具有明显的非线性，可以近似的用指数函数描述。鉴于曲线的分布特点，前述模型中的边界条件均采用指数形式。在图3中还给出了通过模型计算得到的各格点含水率，并将计算值与实测值进行了比较。总体来说，计算值与实测值是比较接近的，说明模型完全具有实际价值，另外，计算得到的分布曲线一般要比实测得到的曲线稍显平滑。

图1 试验装置与求解区域

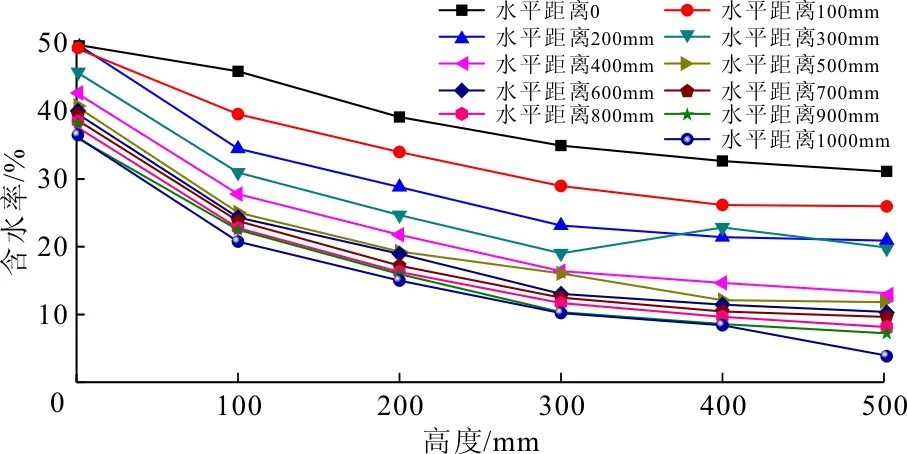
图2 不同水平距离含水率随高度的变化规律

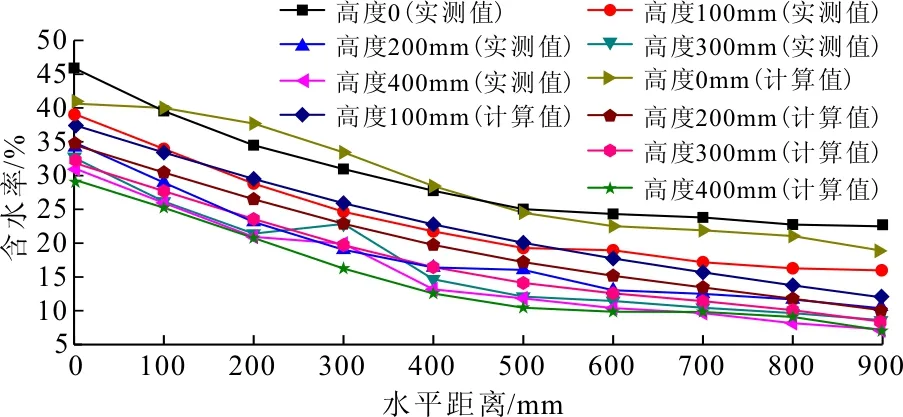
图3 不同高度含水率实测、计算值在

4.2 模型参数的计算结果

4.1节中用模型计算各格点含水率之前，就已知模型中的参数值，所有参数值均利用3.2节所述的原理与过程，通过Matlab7.0编程计算得到，运算中误差的变化如图4所示，从图4中看到，开始时收敛速度较快，然后逐渐变慢，随着迭代次数的增加最后误差趋于恒定值。由计算得到公式中的未知参数取值如下：

α=6.839088379,β=20000.0,

A1=44.22930231,A2=0.0960269445,

A3=979.9613199,A4=20000.0，

A5=4465.81149,A6=0.1204775985,

A7=21.48347685,A8=16768.46475,

D=16177.80965

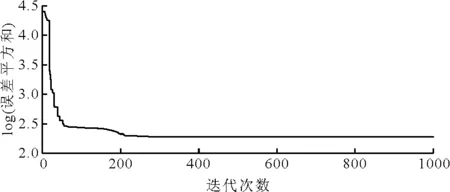
图4 运算误差演化曲线

5 结 论

(1)通过解析方法得到了描述二维非饱和尾矿砂稳态渗流含水率空间分布公式，求解过程从Richards方程的简化开始，方程简化主要包括两个方面，第一是将方程形式简化，简化过程中包括降低维度、由瞬态变为稳态、将未知参数简化为常数或固定函数形式等。第二是将复杂的求解区域简化为矩形，在矩形区域里只要给出边界条件是可以得到方程解析解的。

(2)模型求解所需的边界条件应在参考试验数据的基础上给出，以此来保证求解结果的有效性。求解中引入的参数可通过CPSO算法编制程序利用测量数据得出。算法计算中误差具有明显的收敛性。得出的参数能够很好地拟合全部测量数据。由计算得到的曲线较实测曲线具有明显的光滑性。