岩石孔隙内地下水流动的微观数值模拟研究
2019-11-26苏军伟刘媛箐
苏军伟, 王 乐, 吕 高, 刘媛箐
(1.西安交通大学 人居环境与建筑工程学院, 陕西 西安710049; 2. 西安石油大学 机械工程学院, 陕西 西安710065)
1 研究背景
地下水是地球数量丰度分布广泛的淡水资源,对于人类生产生活均有着重要意义[1]。现阶段,研究者多采用有限元方法、有限差分和观测统计等方法[2-6],从宏观角度解析地下水流动及人类活动对地下水质量及污染物运移的影响。郑灿政等[2]采用MODFLOW软件基于有限差分方法,研究了地下结构物对地下水流场的影响,发现地下结构物不仅影响地下水流场的稳定时间,而且使得迎水面水位上升,背水面水位下降。吴乐等[7]采用有限差分方法对北京西山地区含水层系统进行数值模拟,分析不同开采条件下含水层系统响应特征,发现维持现状开采至2030年,岩溶水水位下降22 m,第四系承压水水位下降约28 m。代锋刚等[8]以山西长治盆地潞安矿区为例, 通过野外调查、相似材料模拟实验和数值模拟手段, 分析了群矿开采驱动下含水层结构破坏对地下水流场的影响。虽然现有研究已经取得了丰硕成果,但目前的宏观地下水数值模拟仅重视模型研究,不重视具体水文地质条件的研究,影响了宏观数值模拟结果的准确性[9]。此外,传统的达西尺度分析无法准确描述复杂结构中的渗流规律以及微纳尺度流动中的非达西效应[10]。
从微观角度上来说,地下水流动于岩石孔隙之中,通过真实岩石孔隙中地下水的流动分析能够为宏观地下水流动提供进一步的认识分析。随着图像学和计算流体力学的发展,通过对岩石进行CT扫描获得物理模型[11-12],并进一步对该模型进行网格划分得到真实的岩石孔隙计算域,结合计算流体力学,使得地下水流动及污染物迁移在真实岩石孔隙内的研究成为可能。近年来,基于真实岩心的数值模拟技术发展迅速,其中,哈佛大学Datta等[13]在微尺度下研究了三维多孔结构内的流体流动行为,发现复杂孔隙结构内流体流动并不是随机的,且沿流动方向的流动速度呈指数分布。斯坦福大学的Roman等[14]采用微型PIV技术测量了孔隙内的单相流动速度,且采用数值模拟验证了实验结果,并对不相融两相流动进行了数值模拟研究。Yang等[15]采用多种数值方法模拟了流体在岩石孔隙内的流动行为,从宏观变量和微观变量两个方面对不同数值方法的模拟结果进行比较。清华大学王沫然等[10]对地下深层岩石微纳米孔隙内气体渗流进行了跨尺度混合模拟,为页岩气勘探开发提供了相关理论支持。Su等[16-17]基于欧拉-拉格朗日架构下,开发了颗粒追踪的精确算法,对真实岩石中的驱油过程进行了多相数值模拟,揭示了真实岩石中多相流动机制及流动行为。以上研究表明了基于真实岩心的流体流动行为研究逐渐展开,且由单相不断扩展至多相,研究结论也进一步解释了宏观尺度研究中观察到的现象[18-20]。
本文从微观角度出发,通过对真实岩心进行扫描,建立真实微观岩石孔隙结构模型,并基于此对地下水在岩石孔隙内的流动进行数值模拟,探讨不同流量及不同出入口位置对地下水流动的动力学行为影响,以期完善地下水流动的微尺度数值模拟方法,为地下水的流动行为提供微尺度解释。
2 数学模型
根据连续介质假设,只要流动特征尺度远大于流体微元尺度,可采用N-S方程描述流动,从目前实验测量看出,连续假设可以应用于10 nm以上的流体流动[21],因此对于微米级真实孔隙尺度,连续介质假设仍然适用。
质量方程:
(1)
动量方程:
(2)
式中:ρ为密度;u为速度;p为压强;ν为黏度。压力和速度耦合采用PISO算法[22]。上述数学模型通过有限体积法进行离散。
3 物理模型及计算方法
本研究中通过岩石扫描技术结合数字图像处理技术得到真实岩石孔隙结构的物理模型,二维真实孔隙尺度岩心的物理模型如图1所示。该模型长、宽分别为0.010 3和0.008 53 m,且模型内分布着多条微米级复杂、曲折、相互贯通的孔隙通道。地下水从左侧区域向右侧区域流动,为更好地说明入口和出口位置,图1(a)中标注的数字1、2、3、4、5、6、7、8分别对应入口1、入口2、入口3、入口4、出口5、出口6、出口7及出口8。
采用非结构化网格对该物理模型进行网格划分,图1(b)中给出了图1(a)中方框区域对应网格的细部划分,显示了在微米级孔隙通道内,网格分布均匀密布。经网格独立性检验,本文选择总量为221 742的网格进行计算。
对不同的注入速度及出入口位置的算例设置如表1所示,算例a、b和c分别探讨相同入口位置不同入口速度下孔隙尺度地下水流动行为;算例b、d及e分别探讨不同入口位置相同流量下孔隙尺度内地下水流动行为;算例f为多入口及出口的算例便于与以上算例的对比分析,其入口流量与算例b一致。水的密度为1 000 kg/m3,运动黏度设置为0.000 001 m2/s。
采用OpenFOAM开源流体力学软件中的icoFoam求解器,设定时间步长为10-6秒,最大库朗数为0.1,各个物理量残差设置为10-6。
4 结果分析与讨论
图2为整个岩石孔隙通道内的速度分布。由图2可以看出,不同区域的地下水流动速度差异较大,尤其是在四个端角附近,流动速度受边界阻滞的影响,流动较为缓慢,且在相邻通道内受孔道大小及两侧压差的影响,流动速度也存在较大变化;此外,在单向封闭孔隙通道——盲道(通道仅存在一个出入口)内地下水流动近乎停滞,以上现象说明真实岩石孔隙通道内的地下水流动具有复杂性和非均匀性。对比图2(a)、2(b)及2(c),发现随着入口速度的增大,岩石中部孔隙内的速度不断增大,而左侧上部区域速度变化差异较小,这主要是由于左侧上部存在着多处不连通孔隙且受边界条件影响,共同形成了流动死区。为了进一步说明不连通孔隙对地下水流动的影响,对图2(a)中方框区域进行了放大分析,详见图4叙述。此外,对比图2(b)、2(d)及2(e),发现随着入口位置的改变,地下水流动的速度分布发生明显变化。当入口位置位于中下部时(图2(d)),对比图2(b),发现岩石孔隙下部区域的流动情况得到改善,下部水流速度明显增高,仅在岩石上部左侧和上部右侧孔隙存在着明显的速度低值区;当入口位置位于中上部时(图2(e)),对比图2(b),发现左侧上部岩石孔隙的地下水流动速度明显增加,且这一变化也体现在中部及中下部区域,仅下部水流速度没有明显变化。这意味着在流量相同的情况下,改变入口位置能够改善微观岩石内的地下水流动情况,且无论是改变入口速度或调整入口位置,单向封闭孔隙通道内的流动情况都无法得到改善。需要说明的是,本算例中出口位置并没有变化。当出口位置上移或下移时,受出口位置的影响,在中部及右侧区域的地下水流动方向将随之变化,并增大出口周边区域的地下水流动速度。图2(f)给出了多入口、多出口下的岩石孔隙结构内水流速度分布,对比同一流量下算例b,发现整个岩石孔隙区域中部的水流速度明显较低,而岩石右上部区域速度有着一定的升高。
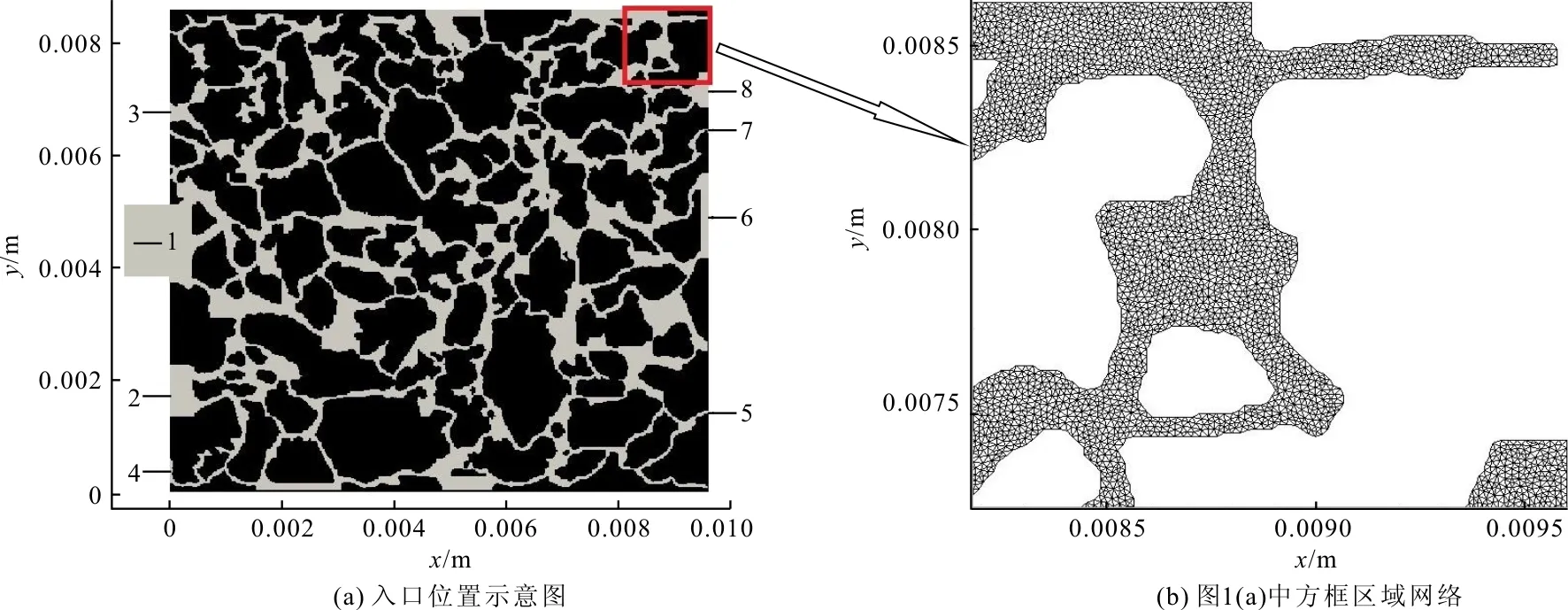
图1 二维真实岩石孔隙结构模型及网格划分

参数算例a算例b算例c算例d算例e算例f入口速度/(m·s-1)0.0010.0020.0030.003010.007360.0009入口位置入口1入口1入口1入口2入口3入口1、2、3、4出口位置出口6出口6出口6出口6出口6出口5、6、7、8
图3进一步给出了孔隙结构内的y方向速度分布,通过设置两个速度区间区分了y正方向和负方向的水流流动行为,间接反映了孔隙结构内水的流动方向。发现所有算例中,在图3(a)方框区域内的y方向速度分布极为接近,差异主要体现在岩石孔隙结构的左侧区域。其中随着流量的增大,对比图3(a)~3(c),发现y方向速度分布没有明显差异,这也意味着入口速度的不断增大并没有明显改变水流在孔隙结构内的y方向流动。而入口位置的改变对岩石孔隙结构内速度分布影响明显,对比图3(b)、3(d)及3(e),发现左侧区域受入口位置改变,速度分布存在明显差异,意味着在这些区域水的流动方向变化剧烈,但受影响的区域明显有限,主要集中于入口周边区域。如图3(f)所示,多入口及多出口下,y方向速度分布与图3(a)~3(c)中的速度分布较为近似,这可能是由于入口1和出口6为孔隙结构面积最大的两个出入口,导致了水流主要经由这两个口流入和流出,这也显示了孔隙结构内水流方向往往受面积大的入口和出口影响。
图4所示为各算例部分孔隙结构速度分布(图2(a)中方框区域放大部分),发现无论入口速度大小、入口位置及出入口数量的改变,位于图中左侧中部区域的单向封闭孔隙通道内(图4(c)方框2区域)的地下水流动速度始终极低;通道内径越小,相对的地下水流速度越高;通道内的地下水流动速度高值位于通道中心,受壁面剪切影响贴近壁面处地下水流动速度较小。此外,在图4(a)、4(b)以及4(c)中部区域(图4(e)方框3区域),随着入口地下水注入速度增大,孔隙通道内流动速度并没有进一步增大,其可能的原因是连接该孔隙的上下两侧通道内地下水流动速度较为接近,没有形成明显的压差,且入口速度的增大也没有改变这一现象,导致该区域速度较低;上部区域(图4(c)方框1区域)由于孔隙通道较细,速度变化较为明显,速度持续增大。
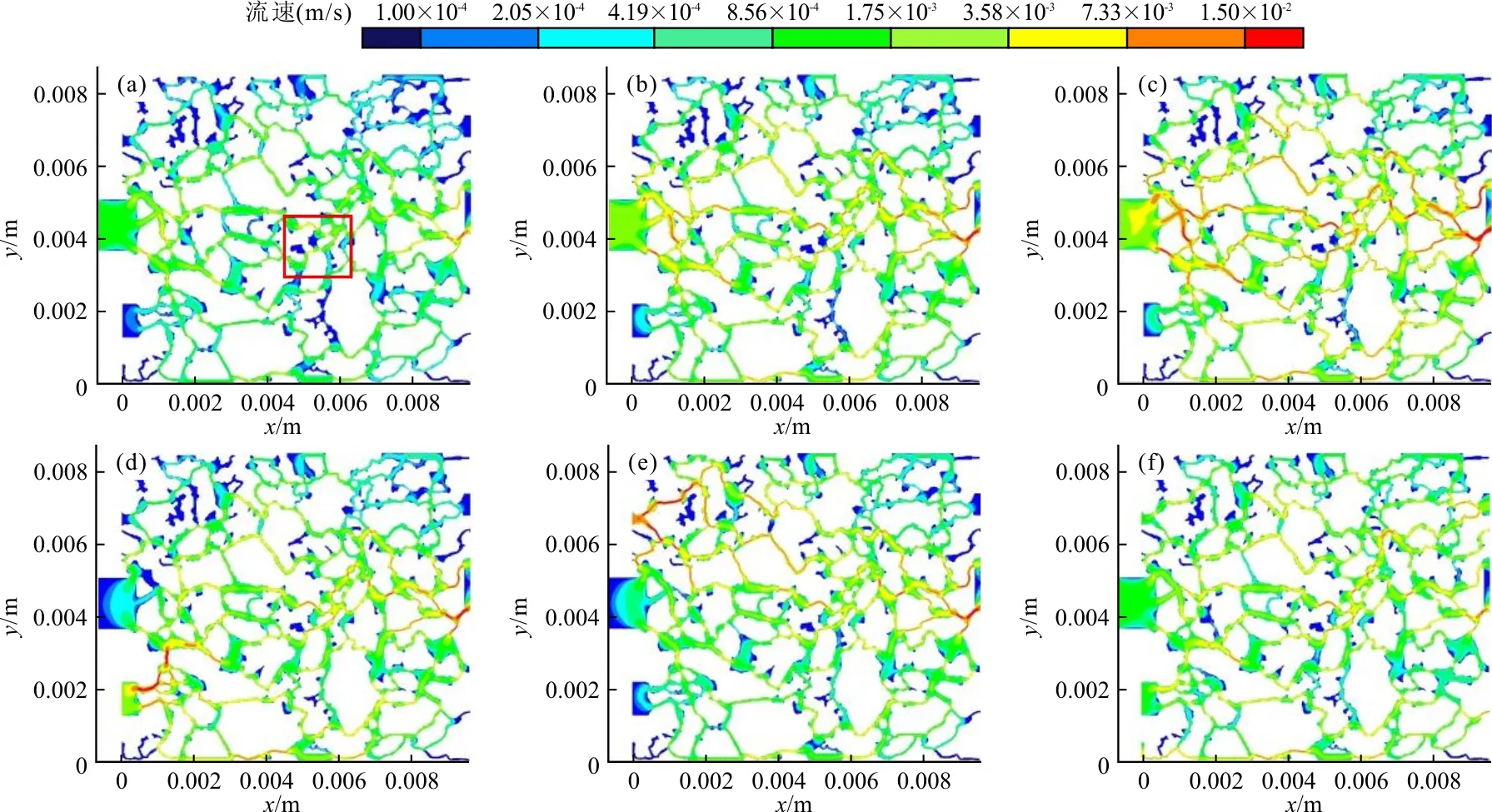
注:图(a)~(f)分别对应算例a~f
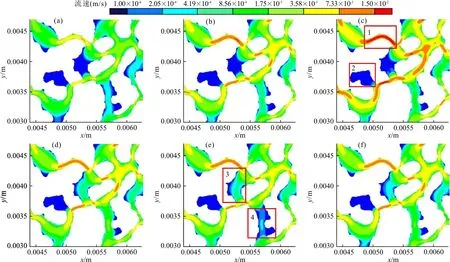
注:图(a)~(f)分别对应算例a~f
对比相同流量下不同入口位置时的算例,如图4(b)、4(d)及4(e)所示,发现地下水流动速度分布区域差异主要体现在图4(e)中的方框3和方框4区域。当入口位置由中部移至下部时,对比图4(b)及4(d),发现方框3区域的地下水流动速度增高,同时方框4区域的地下水流动速度也有一定程度升高;当入口位置由中部移至上部时,对比图4(b)及4(e),发现方框3区域的地下水流动速度明显增大,而方框4区域的速度明显减小。如图4(f)所示,当存在多入口及多出口时,在方框3和方框4区域,对比图4(b),孔隙通道中部水流速度有着少许增大,其他区域速度分布没有明显差异。
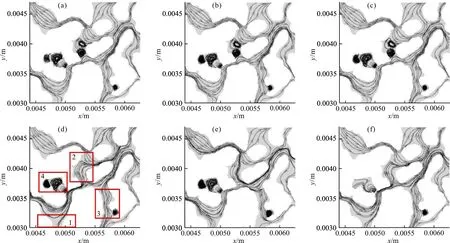
上述讨论分析了孔隙通道内地下水流动的速度分布,但仍然无法精确描述地下水流动方向等行为,为此图5给出了部分孔隙通道内的地下水流线。对比图5(a)、5(b)及5(c),发现随着入口速度的增大,孔隙结构内的流线没有发生明显的差异,意味着水流方向一致;旋涡主要分布于单向封闭孔隙内(对应图5(d)方框4及方框3区域)及上下连通通道内(对应图5(d)方框2区域),这导致了地下水不易流入也难以流出。需要说明的是上下连通的孔隙通道内部旋涡的形成可能是由于流速较为接近,上下没有明显的压差时,该孔隙通道内形成了两个旋涡,影响了地下水向上方和下方通道的流动。
当入口位置发生改变时,对比图5(b)、5(d)及5(e),发现地下水流动方向发生了较大变化。尤其是当入口位置由中部下移,对比图5(b)与5(d),在方框1及方框2区域均发生了明显的流线改变,其中图5(d)中方框1区域地下水由底部向上部流动,而在方框2区域中原有旋涡消失,地下水由下向上流动;当入口位置由中部上移(如图5(e)所示),同样方框2区域内的旋涡消失,此外在方框3区域内地下水流线发生转向,流动方向为由底部向上部流动。值得一提的是入口位置的改变并不影响单向封闭通道内的水流流动形态。当存在多入口及多出口时,如图5(f)所示,其流线与图5(d)接近,而与图5(b)中的方框2和方框1区域有着明显差异。总之,无论改变入口速度、入口位置或出入口数量,岩石孔隙结构内均存在着流动相似区域,而流动方向差异较为明显的区域集中在纵向孔隙通道内。
图6给出了中轴线位置处的x方向速度,其中中轴线位置为x=0.004 45 m。从图6中发现,速度经历着增大、减小、中断的变化过程,这也意味着在每个孔道内,贴近孔道两侧部位受孔壁的影响速度较低,孔道中心速度较高,这与图4中的现象一致。此外,速度的中断也意味着真实岩石内孔道间是不连续的,这也符合岩石的真实地质构造,而现有研究采用多孔介质进行假设时会忽略这一现象。当入口速度不断增大时,对比图6(a)、6(b)及6(c),发现各个孔道内速度值均不断增大且不同孔隙通道内的速度峰值排布序列没有发生变化,仅从流动速度上来说,在靠近y=0.000 2 m以及y=0.003 5 m附近的孔道内存在两处地下水流动速度的较高值,这意味着这两个孔道为地下水流动的优势通道。当改变入口位置时,对比图6(b)、6(d)及6(e),发现不同孔隙通道内的速度峰值排布序列发生变化,尤其是图6(d)中原有的优势通道仅在y=0.000 2 m处,而在图6(e)中y=0.000 2 m、y=0.003 5 m、及y=0.005 2 m处均存在着较高的速度值,这意味着改变入口位置可能会带来地下水流动优势通道的改变。当存在多个入口和出口时,如图6(f)所示,在y=0.000 2 m孔道内地下水流动速度最大;对比图6(b)发现,在y=0.003 5 m处速度减小,但不同孔隙通道内的速度峰值排布序列较为一致。
注:图(a)~(f)分别对应算例a~f

注:图(a)~(f)分别对应算例a~f
图7进一步给出了不同速度权重区间下的占比,其中单个网格内速度权重的计算公式为:速度权重=网格点速度/孔隙孔道内最大速度,根据速度权重的大小归属至0~1中的10个等分区间内得到不同速度权重区间的占比。从图7中可以发现,算例a、b、c的数据基本一致,岩石孔隙内速度权重区间为0~0.1的占比最高,均在0.75以上,意味着地下水流动低速区占据了整个岩石的绝大部分;速度权重区间为0.1~0.2的区域同样占比较高,但明显低于速度权重0~0.1,上述现象意味着低速区在地下水孔隙通道流动速度中占据主导。对比算例a、算例b及算例c,发现改变入口速度的大小,在不同速度权重区间下,未发生明显变化,均为低速区占据主要权重区间。对比算例b、算例d及算例e,发现改变入口位置能够一定程度改变速度权重区间占比,尤其是算例e中,速度权重区间为0~0.1的占比相比于其他两个算例增高了约0.06,意味着低速区的范围进一步扩大,这对于地下水的污染物运移不利。而多入口多出口下,在速度权重区间为0~0.1的占比最低为0.75,明显低于算例b的占比,这意味着增加入口和出口数量能够改善孔隙结构内的水流整体流动情况。
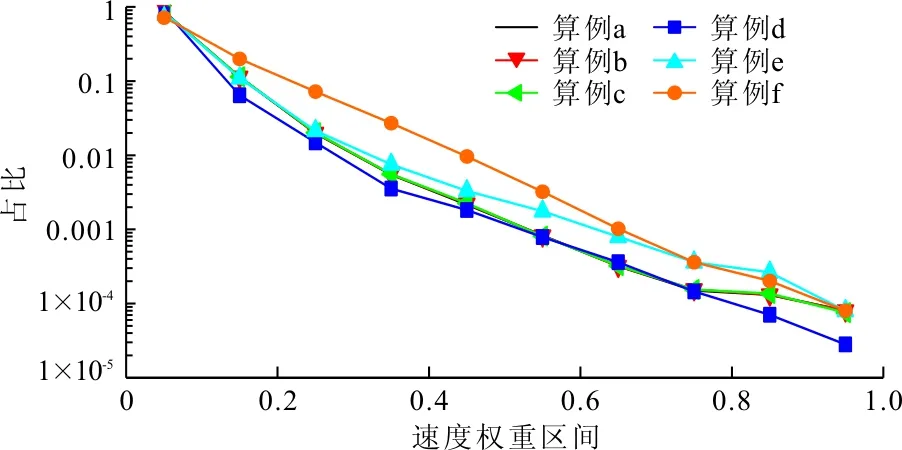
图7 各算例岩石孔隙水流不同速度权重区间占比
5 结 论
本研究针对岩石孔隙内地下水流动行为进行微观数值模拟研究,探讨了不同出入口位置及入口速度对地下水流动行为的影响,主要结论如下:
(1)真实岩石孔隙内地下水流动过程非常复杂,地下水流速呈现非均一性。随着入口速度的不断增大,岩石孔隙内不同的速度权重基本没有差别,但改变着岩石孔隙内的速度大小。其中,单孔隙内成为地下水流动死区,不受外界入口位置及入口速度大小的影响。
(2)入口位置的变化会改变地下水在岩石孔隙中流动的优势通道数量和位置,且能够改变孔隙通道内的流动方向,尤其是能够影响孔隙结构内低速区的分布权重。
(3)多入口多出口下,岩石中部速度降低,地下水流动方向受面积较大的出口和入口影响,不同孔隙通道内速度排布序列没有明显变化,速度权重0~0.1的占比最小。
