基于构件协同工作的平面钢闸门主梁最优梁高研究

杨 勇， 李守义， 刘计良， 肖 阳， 李 浪， 杨 光

(西安理工大学 西北旱区生态水利国家重点实验室, 陕西 西安 710048)

1 研究背景

平面钢闸门是水利工程中普遍采用的门型之一，常用作检修门或事故门，其能否安全运行就显得尤为重要[1-3]。主梁是平面钢闸门的主要受力构件，一般根据闸门跨度和作用水头来选择其形式[3]，其形式以简支式为主，主梁梁高的选择也就成为钢闸门组合梁截面选择过程中的关键，因为选择一个较优的梁高，不仅对梁的整体稳定有利，而且还能减小门槽宽度及钢材用量等。

何运林[4]结合优化设计原理及规范，提出了迅速选择不等翼缘工字钢梁经济梁高的公式和图表；郑圣义等[5]为改善水工钢闸门主梁腹板的应力分布,减小主梁挠度,提出了一种新型的主梁结构即实腹式双拱形主梁；窦国祯[6]运用数学规划的基本原理，给出了确定钢闸门主梁经济梁高的解析图解法和经济梁高的新公式；崔丽萍[7]根据钢闸门主梁的结构形式及受力条件，推导出了弯曲型与剪切型主梁梁高的计算公式；张雪才等[8]建立了钢闸门主梁优化模型，利用MATHEMATICA和MATLAB软件求解，最后给出了对称与不对称工字形简支式钢梁的最优梁高理论计算公式；王正中等[9]首次提出了双悬臂式单轴对称梁最优梁高的理论公式。由此可知，就平面钢闸门主梁最优梁高而言，已有较多研究成果，得到了一系列可直接应用到工程中的确定梁高的理论公式，且文献[8-9]求梁高的公式所需计算参数也较容易得到。但目前在平面钢闸门最优梁高的研究中考虑各构件空间协同工作的研究较少。

本文在以上理论研究的基础之上，考虑主梁与各构件的协同工作，运用三维有限元的方法进行数值模拟计算[10]，得到了平面钢闸门主梁的最优梁高，为平面钢闸门主梁最优梁高的选择提供参考。

2 计算模型

2.1 计算参数

(1)某工程挡水结构为平面钢闸门，其整体结构采用Q235B钢，弹性模量E=206 GPa，重度为γ=78.5 kN/m3，泊松比为0.3；

(2)平面钢闸门尺寸为10.4 m×6.2 m，设计水头6 m；面板厚度8 mm；主梁采用变截面梁，其上翼缘宽140 mm、厚20 mm，下翼缘宽340 mm、厚20 mm，腹板厚10 mm；竖直次梁布置3道，其腹板与主梁腹板同高；边梁上下翼缘厚度均为14 mm，腹板高度由主梁变截面的高度确定。

2.2 三维有限元模型建立

(1)本文选用的有限元分析软件为Ansys软件；

(2)坐标系设定：垂直水流方向为Z轴，向右岸为正；水流方向为X轴，向下游为正；沿高度方向为Y轴，向上为正；

(3)计算模型的单元划分：各构件网格尺寸控制在0.2 m以内；

(4)平面钢闸门的面板、主梁、竖直次梁用壳单元来模拟，水平次梁用梁单元来模拟；面板与主梁、面板与边梁相接处采用TARGE170与CONTA174单元来模拟[11-14]。

(5)约束处理：边梁顺水流向、垂直水流向施加X向和Z向约束模拟闸门槽的约束；底部施加Y向约束来模拟底槛对面板的约束。

有限元计算模型网格划分如图1和2所示。

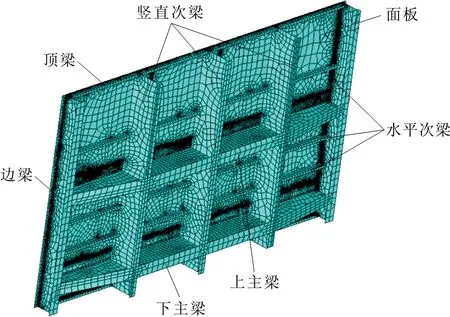
图1 闸门整体结构网格划分

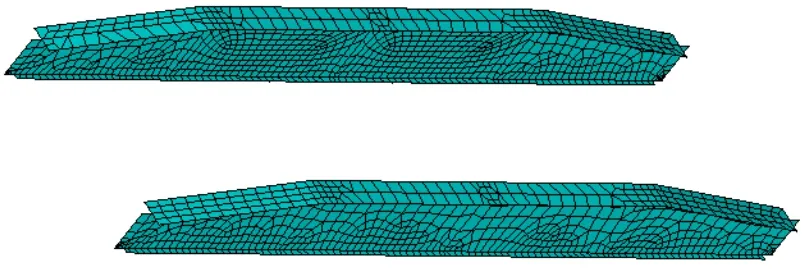
图2 主梁结构网格划分

2.3 计算求解

(1)计算工况：正常蓄水位。

(2)方案设计：为研究主梁梁高对其受力性能的影响，定义量纲归一化的参数K如下：

(1)

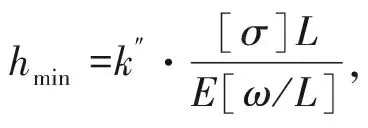
依据定义的公式(1)，本文所选梁高尺寸等差递增，对应的K的取值范围为[1,1.184]，在其区间内选取8种方案，具体如表1所示。

表1 各计算方案K的取值

3 计算结果分析

主梁结构主要承受由面板和竖直次梁传来的水荷载，所以受很大的压力作用，主梁的应力分布主要以平面弯曲应力为主。由于在与边梁相接处会出现小部分应力集中，为避免其对主梁应力分析的干扰，故避开应力集中点。该结构稳定性已满足规范要求。因在设计时上、下主梁所受水压力相等，为方便研究，选下主梁进行分析，且该结构应力分布情况较为复杂，应力大小、方向都在变化，因此本文仅给出关键部位绝对值最大的正应力、切应力及Mises应力。

3.1 强度分析

3.1.1 下主梁上、下翼缘应力分析 各方案下主梁上、下翼缘应力见表2，下主梁翼缘应力随K值的变化见图3。

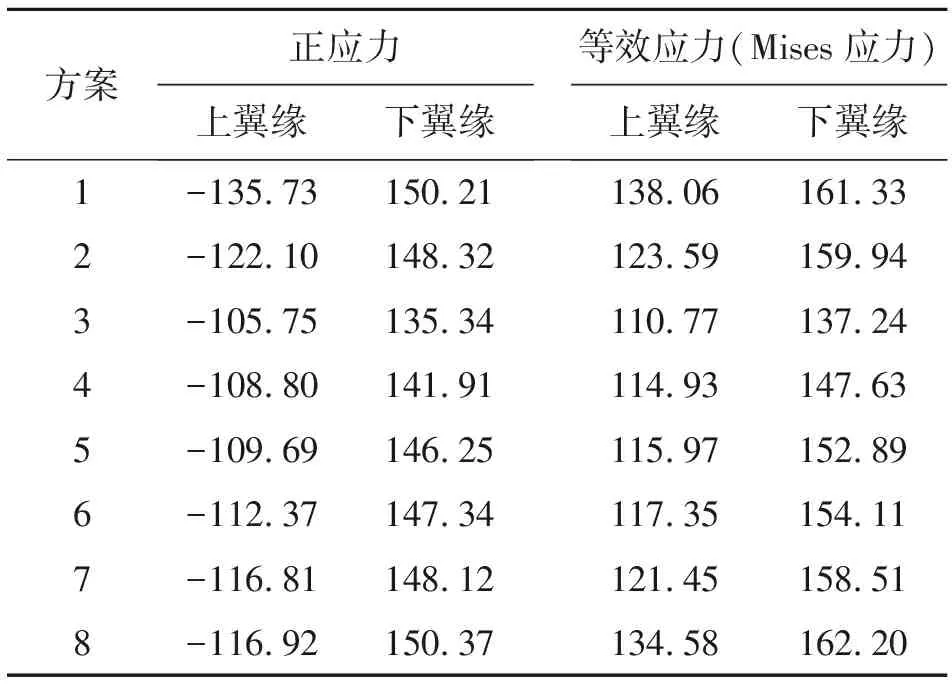
表2 各方案下主梁上、下翼缘应力值 MPa

由表2和图3可知，主梁上翼缘受压，下翼缘受拉，与实际相符。下翼缘拉应力值比上翼缘压应力值大，是由于上翼缘有部分面板来兼作主梁上翼缘的作用，因此上翼缘压应力值较小。随着主梁梁高的增大，上翼缘压应力呈现出先减小后增大的趋势，由135.73 MPa减小到105.75 MPa，减小22.1%，可见当K为1.038时，上翼缘压应力最小；下翼缘拉应力也呈现出先减小后增大的趋势，最大为150.37 MPa，最小为135.34 MPa，减小9.99%，最小拉应力对应的K值也为1.038。该钢结构材料可用畸变能密度理论(第四强度理论)来校核，即为表2中的Mises应力值，可看出Mises应力能够满足容许应力。由计算结果可以看出，由上下翼缘的强度控制的主梁的最优梁高与最小梁高的比值K约为1.038时，能使主梁的上、下翼缘的应力降到最低。

3.1.2 下主梁腹板应力分析 各方案下主梁腹板应力见表3，下主梁腹板应力随K值的变化见图4。

表3 各方案下主梁腹板应力值 MPa

由表3和图4可知：随着主梁梁高的增大，腹板正应力呈现出先减小后增大的趋势，最大为151.68 MPa，最小为145.50 MPa，降幅4.07%，对应K值为1.038左右；腹板切应力也呈现出先减小后增大的趋势，最大为96.6 MPa，最小为86.61 MPa，降幅10.35%。由计算结果可以看出，由腹板强度控制的主梁的最优梁高与最小梁高的比值K也约为1.038左右，与翼缘所得结果相吻合。

3.1.3 应力与位移云图 当选取K值为1.038时，给出平面钢闸门主梁的计算云图，翼缘应力云图见图5，腹板应力云图见图6。

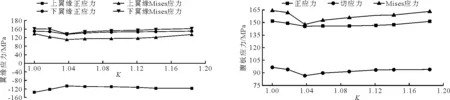
图3下主梁翼缘应力随K值的变化图 图4下主梁腹板应力随K值的变化图

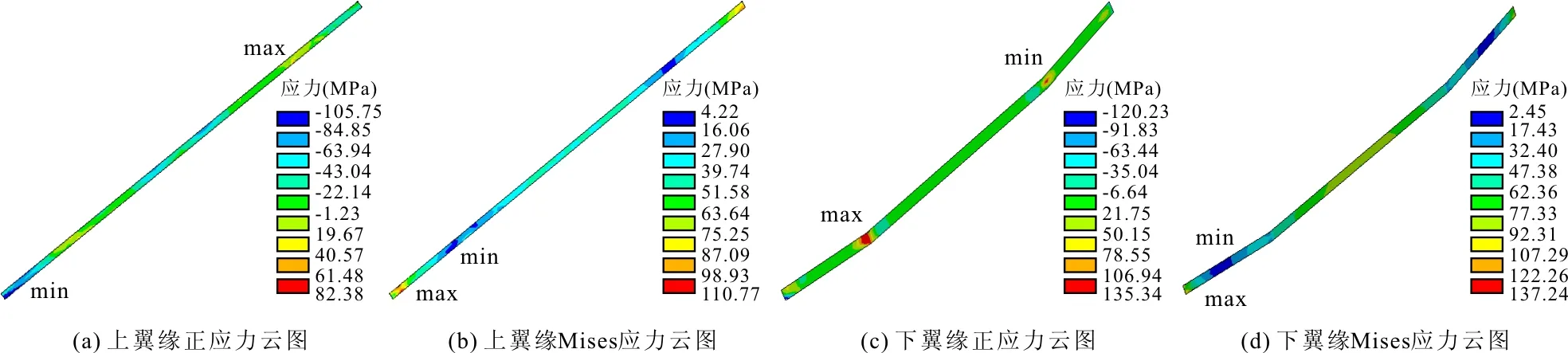
图5 下主梁翼缘应力云图(K=1.038)

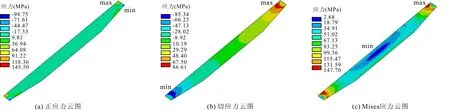
图6 下主梁腹板应力云图(K=1.038)

3.2 刚度分析

下主梁的挠度随K值的变化见图7，下主梁整体位移云图见图8。

由图7可知：随着主梁梁高的增大，主梁挠度呈现出逐渐变小的趋势，各方案中的最大挠度为7.41 mm，最小挠度为5.63 mm，挠度最小值比最大值减小24%。此规律符合工程实际，由于随着梁高的增大，其截面抵抗矩也随之增大，抗弯性能随之增强，因而挠度会随之减小。单从刚度角度看，各方案计算的主梁挠度均控制在规范规定的最小挠度之内，均能满足要求。因此在选取最优梁高时以强度为控制条件。

3.3 讨论

将文献[4]和文献[8]所得的理论最优梁高公式应用到该工程实例中，利用三维有限元的方法建模、求解，针对主梁的不同组成构件(上翼缘、下翼缘和腹板)，将三者的最大工作应力及挠度的计算结果进行对比，见表4。

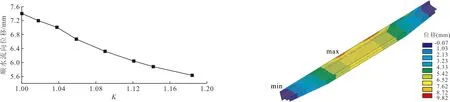
图7下主梁挠度随K值的变化图 图8下主梁整体位移云图

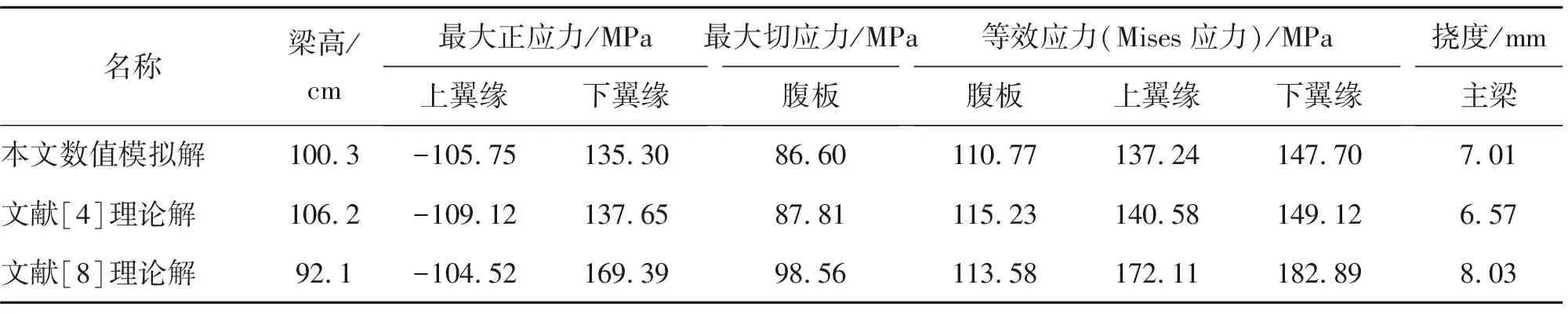
表4 数值模拟解与文献[4]、[8]的理论公式解对比表

由表4可知，本文的上翼缘压应力比文献[4]的压应力减小3.09%，下翼缘拉应力减小1.71%，腹板切应力减小1.38%，本文的梁高比文献[4]的小5.56%；比较本文与文献[8]的计算结果，本文的上翼缘压应力比文献[8]的压应力增大1.18%，下翼缘拉应力减小20.13%，腹板切应力减小12.13%，文献[8]的梁高较小，但参考规范给定的Q235钢的容许应力，文献[8]主梁的某些构件的最大工作应力超过了规范规定的容许应力；三者的挠度均较小且都满足规范要求。

基于三维有限元的方法进行数值模拟，对理论公式没有考虑各构件的空间协同工作这一不足进行补充。本文所得的主梁最优梁高能使各构件的受力性能得到较好的发挥，既能充分利用材料，又有安全富裕，可作为平面钢闸门最优梁高理论模型的补充。

4 结 论

本文采用三维有限元分析法，研究了平面钢闸门主梁梁高对腹板、翼缘等关键部位应力和变形的影响，得到以下结论：

(1)对于平面钢闸门这类受力复杂的空间结构而言，考虑主梁与其他构件的空间协同工作是有必要的，能更加真实地反映结构的受力特征。

(2)最小梁高与经济梁高之间存在一个最优梁高，该梁高与最小梁高比值约为1.038，与理论公式计算的最优梁高相比，可减小主梁翼缘、腹板等构件的应力，使各构件受力更为合理。

(3)钢闸门的主梁是主要的受力构件，合理选择梁高直接关系到钢闸门的经济性及安全性，本文所得的最优梁高可为工程设计提供参考。