弧形钢闸门支承钢梁横向加劲肋布置研究

肖 阳， 李守义, 2， 刘计良,2， 杨 勇， 张紫璇， 李 浪

(1. 西安理工大学 水利水电学院， 陕西 西安 710048； 2.西北旱区生态水利国家重点实验室， 陕西 西安 710048)

1 研究背景

弧形钢闸门支承体形式主要为钢筋混凝土锚块式和钢筋混凝土深梁式[1]。钢筋混凝土锚块式支承形式存在着受力钢筋多、不易布置、在闸墩颈部出现较大的拉应力且支铰定位精度不易控制等缺点；钢筋混凝土深梁式支承形式虽然整体稳定性能好、刚度大，但工程量大，且有在闸墩颈部出现较大拉应力的缺点。为了克服上述缺点，大型弧形钢闸门的支承体采用薄壁钢梁结构，其具有结构形式简洁、力的传递路径明确、施工装配更加准确快速，可减少闸室空间，节省工程量并能有效改善闸墩受力性能的优点。

支承钢梁的安全直接关系到弧形闸门的正常运行。与建筑结构的支承钢梁不同，弧门支承钢梁由于要承担巨大的水推力及锚索预应力，因而设计具有合理结构形式的弧门支承钢梁至关重要。目前，国内外诸多学者对钢梁的力学性能都进行了深入研究[2-8]，加劲肋是保证钢梁局部稳定性及改善强度和刚度的重要构件，目前对钢梁力学性能的研究中不乏对加劲肋的深入分析。Maiorana等[9]研究了各种受力状态下桥梁腹板纵向加劲肋的线性屈曲，并提出具有实用价值的形状和优化位置方案。Perchikov[10]利用加劲板挠度场表达式的渐近展开式，推导出了高柔性和高刚性加劲板的全局最优加劲布局。Liu等[11]选取里兹能量法得到组合梁受旋转约束支承影响的纵向加劲肋临界刚度和最优位置的计算公式。Zhang等[12]推导出矩形加筋板在非均匀荷载作用下的局部屈曲非线性特征方程，并指出纵向加劲板的最优设置位置。石雪飞等[13]研究了加劲肋布置对工字钢组合梁桥结构性能的影响。

上述成果大多集中于建筑钢结构方面，而对弧门支承钢梁合理布置方面的研究较少，目前《钢结构设计标准》(GB50017-2017)仅规定横向加劲肋的最小间距为0.5h0，最大间距为2h0(h0为腹板高度)[14]，而横向加劲肋构造形式及其间距的不同都会影响到支承钢梁的力学性能[15]，因此，有必要对弧门支承钢梁横向加劲肋布置进行详细的分析，避免在设计中造成不必要的浪费或不安全。针对这一问题，本文结合工程实例通过对比分析多种横向加劲肋间距的支承钢梁的应力分布规律，得出支承钢梁横向加劲肋间距的合理布置区间，为弧门支承钢梁的设计提供参考。

2 计算模型

为了研究支承钢梁横向加劲肋合理布置问题，本文以某工程大型弧形闸门支承钢梁作为研究对象进行分析。该工程闸坝结构堰顶高程50.0 m，两孔闸门孔口尺寸均为9.0 m×17.0 m(宽×高)，钢梁作为弧形工作闸门的支承体，采用预应力锚索固定钢梁。支承钢梁采用Q345钢，梁高3.7 m，跨度15.0 m，钢梁结构图如图1所示。闸门挡水状态时单侧弧门推力为P=28 000 kN。中墩厚度5.0 m对称布置30束锚索，边墩厚度4.0 m布置20束锚索，单束锚索永存吨位4 000 kN。

运用ANSYS有限元软件建立三维模型见图2、3，有限元模型共计251 374个单元，196 138个节点。采用solid65实体单元模拟预应力闸墩和地基，闸墩选用C30混凝土，弹性模量为30.0 GPa，混凝土容重为24.0 kN/m3，泊松比μ为0.17。采用shell181单元模拟钢梁结构，支承钢梁选用Q345钢，弹性模量为206.0 GPa，钢材容重为78.5 kN/m3，泊松比μ为0.3。采用link8单元模拟预应力锚索结构，预应力锚索选用1×19S-17.8-1770钢绞线，钢绞线公称面积为208 mm2，弹性模量为195.0 GPa，钢绞线容重为79.4 kN/m3，泊松比μ为0.3。

基础底面固结，基础四周法向约束，闸坝上下游、顶部及左右横缝面均按自由边界处理。

计算模型应用的坐标系为：坐标原点在左边墩外侧上游底面，闸室轴线方向为X轴方向，向右岸为正；水流方向为Y轴方向，向下游为正；沿高度方向为Z轴方向，向上为正。

3 加劲肋的合理布置

钢梁的局部稳定性是指当压应力或剪应力达到钢材的临界应力时，钢梁翼缘或腹板会突然偏离原有的平面位置而发生显著的波形屈曲，钢梁即丧失局部稳定性[16]。

为探索支承钢梁横向加劲肋的合理布置间距，针对控制工况在满足局部稳定性的条件下，设置5类加劲肋间距布置方案并进行对比分析。为便于研究，各方案均假定仅有横向加劲肋间距变化而钢梁其他结构形式均不改变，分别计算分析控制工况下各设计方案支承钢梁的力学性能。

各方案支承钢梁横向加劲肋间距设置如下。

方案1： [1/2，1)h0；方案2： [1/3，1/2)h0；方案3： [1/4，1/3)h0；方案4： [1/5，1/4)h0；方案5： [1/6，1/5)h0。其中，h0为腹板高度。

为便于分析，建立局部直角坐标系，以梁横截面的宽度方向为X轴，上腹板指向下腹板方向为正；梁轴线方向为Y轴，向右岸为正；梁横截面的高度方向为Z轴，下翼缘指向上翼缘方向为正。

3.1 强度分析

不同方案支承钢梁各构件绝对值最大的应力计算结果见表1。

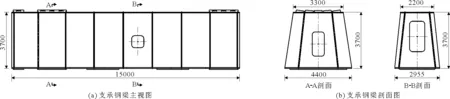
图1 某工程弧形闸门支承钢梁结构图(单位：mm)

图2整体有限元模型 图3支承钢梁有限元模型

表1 不同方案支承钢梁各构件应力值 MPa

注：切应力正负号代表方向，遵循弹性力学中切应力正负号规定。

分析表1数据可知，方案1的支承钢梁翼缘及横向加劲肋最大应力已超过钢材允许应力(205 MPa)，不满足规范要求[17]。随着支承钢梁横向加劲肋间距的缩小，支承钢梁上、下翼缘的应力值明显减小，且上翼缘的应力值均大于下翼缘的应力值。横向加劲肋间距从 [1/2，1)h0缩小至[1/6，1/5)h0时，上翼缘第一主应力降低64.3%，Mises应力(等效应力)降低61.9%，下翼缘第一主应力降低65.7%，Mises应力降低45.5%，可见改变支承钢梁横向加劲肋间距能有效改善其上、下翼缘应力。

随着支承钢梁横向加劲肋间距的缩小，支承钢梁腹板的应力值有减小趋势但变化不明显。横向加劲肋间距从 [1/2，1)h0缩小至[1/6，1/5)h0时，腹板第一主应力降低5.3%，Mises应力降低12.2%，切应力降低9.4%，可见改变支承钢梁横向加劲肋间距对改善支承钢梁腹板应力影响较小。

随着支承钢梁横向加劲肋间距的缩小，支承钢梁横向加劲肋的应力值减小明显。横向加劲肋间距从 [1/2，1)h0缩小至 [1/6，1/5)h0时，横向加劲肋第一主应力降低55.4%，Mises应力降低55.3%，切应力降低56.8%，可见改变支承钢梁横向加劲肋间距能有效改善钢梁横向加劲肋应力。

比较各个方案下支承钢梁各构件应力值，绘制不同加劲肋间距各构件绝对值最大的应力变化图，见图4～6。

由图4～6可知，缩小横向加劲肋间距能有效改善支承钢梁上、下翼缘及横向加劲肋的应力，但对腹板应力影响很小，是由于横向加劲肋主要是保证腹板的局部稳定性。横向加劲肋间距为 [1/3，1/2)h0时，支承钢梁的应力最接近钢材容许应力，此时材料的性能得到最大程度的发挥，达到最优结构性能。

3.2 刚度分析

考虑钢梁的实际受力情况，主要分析其沿顺水流方向的挠度。梁的挠度由其轴线的位移来确定，但是由于支承钢梁结构非常复杂，通过确定梁轴线位移的方式来确定挠度非常困难，对于此类型的钢梁，通常可由上翼缘的位移来确定挠度。考虑到钢梁自身以及与闸墩的变形协调的问题，取上翼缘端部顺水流方向的位移u0为梁端位移，取上翼缘跨中顺水流方向的位移u1为刚度验算点的位移，则钢梁顺水流方向的最大挠度为：

umax=|u1-u0|

(1)

支承钢梁横向加劲肋间距与钢梁最大挠度的关系曲线见图7。

图4不同加劲肋间距各构件第一主应力变化图 图5不同加劲肋间距各构件Mises应力变化图

图6不同加劲肋间距各构件切应力变化图 图7加劲肋间距与钢梁最大挠度的关系曲线

图8 方案2支承钢梁各构件应力云图

由图7可知，随着横向加劲肋间距的减小，支承钢梁最大挠度也不断减小，且各方案计算的支承钢梁挠度都能满足规范规定的最小挠度要求。钢梁横向加劲肋间距从 [1/2，1)h0缩小至 [1/6，1/5)h0时，钢梁最大挠度从2.45 mm减至1.85 mm，降低了24.5%，可见缩小加劲肋间距能有效降低钢梁挠度。由于横向加劲肋间距为 [1/6，1)h0时支承钢梁均能满足规范规定的最小挠度要求，故结合其强度要求，横向加劲肋间距为 [1/3，1/2)h0时，支承钢梁整体稳定性满足规范要求，且钢梁材料能够发挥较优结构性能。由于两孔闸门支承钢梁结构形式及工况相同，故仅给出单孔(左孔)钢梁方案2的各构件Mises应力及切应力云图见图8。

由图8可知，支承钢梁上应力大致以钢梁中心线为轴对称分布，弧门支绞及预应力锚索位置的拉应力最大，腹板及横向加劲肋大部分拉应力较小。

4 结 论

在保证稳定性的前提下，通过改变支承钢梁横向加劲肋布置间距，分别对支承钢梁的强度和刚度进行研究分析，得到以下结论：

(1)支承钢梁横向加劲肋间距对钢梁翼缘和横向加劲肋的应力影响明显，对腹板应力影响不大，因此，可通过减小支承钢梁横向加劲肋间距改善翼缘及横向加劲肋应力。

(2)支承钢梁各构件应力大致以钢梁中心线为轴对称分布，其中弧门支绞和预应力锚索位置的拉应力最大。

(3)建议支承钢梁横向加劲肋间距为[1/3，1/2)h0，在此区间内钢梁材料的性能得到充分发挥，支承钢梁强度、刚度及稳定性满足规范要求，兼具经济性和合理性。本文建议的横向加劲肋间距可为弧门支承钢梁的设计提供参考。