基于响应面分析的隧洞开挖过程优化设计研究

南 轩， 刘艳慧， 孙语晨， 张玉波， 张明飞

(1.云南农业大学 建筑工程学院， 云南 昆明 650000； 2.云南省高校城乡水安全与 节水减排重点实验室， 云南 昆明 650000)

1 研究背景

鉴于龙开口水电站一期工程中隧洞施工存在的侧壁坍塌问题，目前国内外隧洞的开挖主要研究在隧洞的爆破和开挖方式及支护方面，貊祖国等[1]研究不同开挖方式下的隧洞引水过程中温度应力耦合；章诚等[2]研究了连续爆破下的围岩应力的变化；于小朋等[3]研究隧洞群的支护方式，但对于隧洞开挖过程中围岩受力的变化情况研究较少，因此本文基于ANSYS APDL隧道分步开挖数值模拟方法对水电站二期设计中与一期的7#和9#塌方隧洞岩体实际参数相似的1#隧洞，采用D-P屈服准则描述岩体的关联流动程度通过测定单轴抗压、抗剪及相关参数[4-10]，应用生死单元法通过APDL编写单元命令实现分部开挖(第1步实现隧洞顶部开挖、第2步实现隧洞洞身上半部分的开挖、第3步实现洞身下半部分的开挖)了解其开挖过程应力和位移的变化情况，并通过参数设计试验进行优化分析[11]，最终确定1#隧洞最优设计方案保证侧壁的应力最小,减小塌方的可能性。

2 隧洞开挖数值模拟设计

2.1 D-P准则的应用

1#隧洞长78.60 m，设计流量1.43 m3/s，加大流量1.79 m3/s，穿越地层为古生界二叠系上统玄武岩组上段(P2β3)致密状玄武岩夹凝灰岩，隧洞最大埋深约30 m，进、出口段属于V类围岩，洞身段围岩以IV类为主，围岩局部稳定性差。岩体描述在之前的研究中通常采用M-C准则但其收敛性较差，通过大量的修正和计算表明D-P准则能够更加完整和准确地描述岩体在开挖过程中的破坏和变形情况。Drunker-Prager准则是在M-C准则和塑性mises准则的基础上扩展得到，可表示为：

(1)

式中：I1为应力张量第一不变量；J2为应力偏量第二不变量，偏应力张量第二不变量J2的大小可用来判断物体所处的弹塑性状态；α、k均为与材料的黏聚力和内摩擦角φ有关的参数 。

I1，J2可通过主应力表示为：

I1=σ1+σ2+σ3

(2)

(3)

式中：σ1、σ2、σ3分别为最小主应力、中间主应力、最大主应力，MPa。

与M-C准则相比，D-P准则不仅考虑了中间主应力对材料的屈服影响，通过实际岩体的剪切强度和抗压强度以及内摩擦角考虑了静水压力和中间主应力，能更加全面地反映隧洞开挖过程中岩体的变形和应力的变化。

根据D-P的屈服流动准则在岩体塑性变形阶段其变形量满足：

(4)

在整个弹塑性屈服的阶段，其总的应变量为弹性形变和塑性形变的总和:

(5)

2.2 生死单元法的应用

在隧洞施工过程模拟中，需要对模型进行合理的设置，按照龙开口水电站二期1#隧洞的实际模型进行1∶1的建模，在施工过程中分为多步开挖，施工过程中每一次的开挖就相当于去掉这个开挖单元，在建模过程能去掉有限单元的方法有很多，但由于开挖过程中每次开挖都对后面的开挖过程有较大的影响，因此需要用生死单元法，生死单元法可以记录前一施工步结构的变形状态、应力、位移，并可将前一施工步中的变形和应力传递给下一步的施工。

2.3 有限元模型的建立

输水隧洞的模型尺寸为1.5 m×1.8 m，按照龙开口隧洞处山体形状实测和设计施工尺寸要求进行设置，在相应的边界处进行加密保证网格质量良好，网格质量为0.84时网格数量为1 232 987，经计算满足网格无关性的要求(网格继续加密对计算结果无影响)，保证数值模拟结果的准确性。有限元模型如图1所示。

2.4 实验数据确定和设计

由于ansys模拟过程中需对岩体材料属性进行Drunker-Prager屈服准则设计，因此需要测定出龙开口1#隧洞的抗压强度与变形量的关系和抗剪强度。基于实验和相关文献得到如表1的龙开口水电站1#隧洞岩体的相关参数数据[13]。

上述参数完全能够满足Drunker-Prager屈服准则设计下数值分析过程中岩体的变化情况。

3 数值模拟结果分析

数值模拟中采用生死单元法，这有助于详细了解施工过程中应力、应变、变形等的变化情况，首先分析开挖过程中的岩体变形情况，开挖过程中岩体变形云图如图2所示。

图1 龙开口水电站1#隧洞岩体有限元模型

表1 龙开口水电站1#隧洞岩体特性参数

图2 龙开口水电站1#隧洞开挖过程中岩体变形情况

由图2可以看出，在未开挖阶段，整个岩体在重力加速度作用下产生变形，随着上部岩体的开挖，隧洞周围的岩体出现了变形不均匀的情况，隧洞顶部的岩体变形量远大于底部的变形量，而且隧洞底部与顶部的变形在方向上也是不同的。顶部的变形主要是由重力引起的向下的位移，当岩体较松软时顶部塌陷的机率较大，底部的岩体受到两侧的围岩挤压之后形成向上的位移，同时可以发现在侧边处的变形量较大，侧边处易于塌方，这与实际的施工中塌方主要是侧壁处应力较大并且龙开口输水隧洞岩体较松软的情况基本一致，与相关的工程实际和相关文献相吻合[12-13]。

由图2可以看出，在隧洞顶部处变形出现峰值，监测隧洞顶部的变形量能更加详细地了解开挖的进程。随着开挖步的进行，隧洞顶部的变形量逐渐增大，从未开挖时最大变形量5.894×10-5m到第1步开挖之后的最大变形量6.502×10-5m，再到第2步开挖时为1.071×10-4m，最后一步开挖后为1.098×10-4m。可以通过隧洞沿程的变形曲线了解到每一步开挖过程的变化情况，如图3所示。

由图3可以看出，开挖过程中第1步开挖之后与未开挖的顶部变形量相差不大，这主要是由于弧顶的开挖量相对较小，但是在第2步开挖之后的顶部变形量远大于第1步开挖之后，同时第3步开挖之后的顶部变形量与第2步开挖之后顶部的变形量相差不大。

隧洞的稳定性与其隧洞围岩处所受到的应力有密切的关系，通过应力云图可以了解其应力的分布情况，并且得到其侧边处的应力变化情况，应力云图如图4所示。

图3 开挖过程中隧洞顶部沿程变形曲线

图4 隧洞开挖过程中应力变化云图

由图4可以看出，随着开挖进程的深入，岩体逐渐出现应力集中的现象，其应力集中在隧洞的附近的围岩之中，在隧洞的侧壁面中间位置处的应力出现最大值，同时根据沿程应力曲线和沿程应变曲线(图5)可以发现，在隧洞第2步开挖完成后，整个岩体应力峰值和应变峰值变化较大，应力峰值从8.72×105Pa增加到1.47×106Pa，应变峰值从2.955×10-5m增大到4.906 ×10-5m，结合整个过程中变形情况可以确定，在整体的开挖过程中第2步开挖对应力、应变的影响最大。

图6为整个开挖过程中隧洞侧壁的应力和变化矢量变化。由图6可清晰地了解应力和变形参量在隧洞每一步开挖完成后的变化情况，未开挖时，隧洞壁面矢量方向沿隧洞反向方向偏下，在第1步开挖之后，其矢量方向基本没有太大的变化，随着第2步开挖的进行隧洞周围的岩体的应力、变形的矢量方向发生了显著变化，其方向已经出现偏转，随着开挖继续进行其矢量的方向与侧壁面夹角增大，与侧壁面在实际中的坍塌方向一致，在整个开挖过程中隧洞围岩处的应力、变形的矢量方向在不断变化最终与侧壁形成夹角并指向隧洞内部，若隧洞施工过程中没有及时支撑，或者岩体较软时易于形成侧边岩体塌方。

通过模拟与分析隧洞开挖过程中围岩的形变、应力、应变等的变化，可以了解到在开挖过程中隧洞的塌方主要是由于侧壁处的应力、应变、变形等增大并且其矢量方向从侧壁面向外逐渐转变为从壁面向内，如何在施工中减小或改善这种状况，尤其是在开挖的岩体所对的Drunker-Prager屈服准则以及非关联流动与各向同性硬化确定的情况下，如何减小其坍塌尤为重要。目前可靠性分析开始被大量运用在结构和工程的失效、疲劳、破坏等方面[14-18]，通过前人在工程可靠性方面的研究分析，本文将进一步运用响应面分析和优化对龙开口水电站1#输水隧洞侧壁应力和变形提出改善意见。

图5 隧洞开挖过程中应力及应变沿程变化曲线

图6 整个开挖过程中隧洞侧壁应力和变形的矢量变化

4 可靠性及优化设计分析

输水隧洞的可靠性分析和优化设计可以保证隧洞耐用程度和降低坍塌机率。随着计算机仿真技术的发展，试验设计的范围和结果更加准确，可通过评价试验因素、确定最佳试验参数组合、分析输入参数和输出参数之间的关系、构建回归方程和近似模型等方法提高工程设计的稳定性，本试验选用中心组合设计(central composite design)由2k全因子设计、轴点设计与零水平的中心点重复试验3部分构成，应用各影响因子的二次多项式来预测其对评价指标的作用。该方法扩展了试验设计空间并得到高阶信息，能够给响应面近似模型提供样本数据，具有设计简单、试验次数少、预测性好等优点，在优化设计中由于山体中的岩体和土体为确定的参数，因此只能对隧洞的埋深、断面的长宽尺寸、隧洞的长度进行相应响应面优化和修改。

响应面分析法，即响应曲面设计方法(Response Surface Methodology，RSM)，是利用合理的试验设计方法并通过试验得到一定数据，采用多元二次回归方程来拟合因素与响应值之间的函数关系，通过对回归方程的分析来寻求最优工艺参数，解决多变量问题的一种统计方法，响应变量y与各输入变量xi的关系可用简单的代数形式表达出来：

(6)

当通过中心组合试验获得M个样本点对应的响应量y=(y(1),y(2),…,y(M))后，利用最小二乘法得到系数矩阵：

β=(θTθ)-1(θTy)

(7)

式中：θ为响应面样本矢量点，可以表示为：

(8)

结合公式(6)～(8)可得二阶响应面近似模型的表达式。

以龙开口水电站1#隧洞尺寸设计为优化对象，将ANSYS数值模拟计算和响应面方法相结合，对侧壁应力和变形进行优化分析。

4.1 输水隧洞设计参数敏感性评价

输水隧洞设计主要参数包括隧洞的埋深、断面的长宽尺寸、隧洞的长度等，要了解这些参数能对应力、变形产生多大的影响，灵敏性分析方法(定量分析某一组研究数据对某些因数响应值变化的分析技术，实质是逐步改变相关变量值以了解关键指标受这些因数影响的规律)能准确分析各因素的权重，是确定因数对结果影响的重要评价方法。在多目标优化(MOGA)方法中很难求出解析解，这里借鉴故障树分析法中计算基本事件临界重要度的方法来进行参数的敏感性评价分析，用S表示敏感度[19-21]，定义为：

(9)

式中：Δyi为应力峰值的变化量，Pa;y0为设计模型下的隧洞侧壁应力峰值,Pa;Δxi为试验中某因数改变量;x0为设计模型对应因数参数。S越大表明应力对该因素的敏感度越高，因此借助敏感度可以了解各因素对应力的相对影响程度，以选出最大的不确定因数。

表2为通过计算得出的隧洞几何参数敏感度：

从表2各因素对应力峰值的敏感度可以看出，隧洞的长度对侧壁的应力峰值无影响，隧洞埋深对应力峰值有较大的影响，隧洞宽度对应力峰值的影响为负相关，因此隧洞长度为无关变量，在设计时不考虑隧洞长度的影响。

4.2 中心复合设计方法的应用

在响应面的试验中应用Design Expert软件采用中心复合试验设计方法，对隧洞几何尺寸因素进行试验设计，见表3。试验总次数为20次,其中14个为外部分析点，6个区域中心点，能够在重复计算中降低误差[22-26]。

表3 中心复合设计试验各因素编码水平

4.3 响应及优化设计结果

中心复合设计试验结果见表4。

将试验结果的数据代入二阶响应面试验近似模型拟合后得到应力峰值基于实际因子水平的回归方程,可表示为：

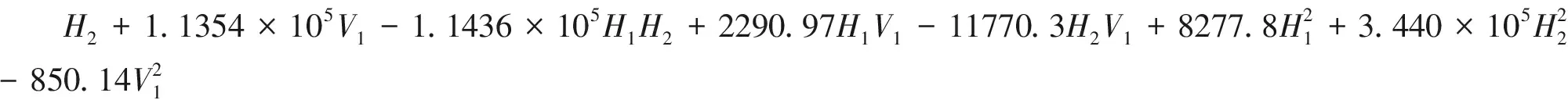
(10)

(11)

相关系数为完全拟合的度量值，反映了响应面与试验数据的相符合程度，要在0.9以上才能保证拟合效果。

(12)

表4 中心复合设计试验结果

4.4 影响应力峰值各参数间交互作用结果分析

试验将隧道侧壁应力作为研究隧洞坍塌问题的主要考察指标，影响侧壁应力峰值的各参数之间交互作用下的侧壁应力峰值变化趋势见图7。参数包括隧洞截面长度H1、截面宽度H2和埋深V1。

从图7中的各因素面的斜率情况可以清楚的了解到，对于隧洞侧边的应力峰值大小，从影响效果上来看是隧洞埋深最大、隧洞截面宽度次之、隧洞截面长度影响较小；从响应面分析结果可以看出，所有的参数与应力峰值之间均处于线性，仅仅是响应程度不同，这也表明在隧洞的设计过程中，在设计许可的范围内尽可能减少截面长度、增大截面宽度，从而保证最终形成的侧壁应力最小并且降低龙开口水电站1#隧洞松软岩体的坍塌机率，使输水隧洞保持良好的稳定性。

为了综合考虑实际施工过程中的参数设计，在优化过程中沿对角线选取外部分析点，由于隧洞的埋深与山体的位置以及水库的位置相关且不易改变，因而在不改变埋深的情况下选取：隧洞截面长度H1=1.35 m和隧洞截面宽度H2=2m、隧洞埋深V1=30 m、隧洞长度L1=78.6 m。

在ANSYS中按照优化前的开挖步骤和方法求解并与优化后的应力与变形曲线进行对比，可以发现整个隧洞侧壁的沿程应力峰值在初始设计尺寸下为1.4159×106Pa，优化尺寸设计后的侧壁沿程应力峰值为1.2741×106Pa，侧壁沿程应力峰值下降了10.01%；同时对沿程应变峰值进行对比,初始设计的应变峰值为4.7053×105，优化后的沿程应变峰值为4.2313×105，侧壁沿程应变峰值下降了10.07%，整体的变化情况与之基本相同。具体如图8所示。

表5 应力峰值回归方程的方差分析

图7 隧洞各几何参数之间交互作用下的应力峰值变化趋势

图8 中心复合试验优化前后应力及应变沿程变化曲线

5 结 论

在分析隧洞开挖过程中隧洞内部的岩体受力和变形时，采用生死单元和数值分析相结合，得到内部的岩体受力情况；同时将敏感性评价分析和响应面法应用于隧洞内部壁面处沿程受力变化情况的优化，选取对受力情况有影响的几何参数，分析各影响隧洞沿程受力参数间交互作用的结果，确定符合隧洞设计要求的最优化参数组合。得到如下结论：

(1)在生死单元法开挖的过程中，从第1步开挖完成到第2步开挖完成，这个阶段隧洞侧壁岩体受到的应力在大小和方向上均发生了极大的变化，应力值从9.7×105Pa增加到1.467×106Pa，其方向从沿侧壁向外转变为沿侧壁向内，此变化极大地增加了隧洞坍塌的可能性。

(2)应用中心复合设计的方法对选取的3个敏感度较高的参数进行试验设计，建立了隧洞沿程应力应变的多元回归模型，同时采用方差分析验证了模型的拟合度。结果表明：回归模型能够准确地反映影响参数与响应值之间的变化关系，并且对实际情况拟合良好。

(3)通过建立的多元回归模型求解，得到了截面尺寸在隧洞设计要求内的最优组合设计参数，在ANSYS中验证之后，发现比原始模型设计得到的沿程应力峰值降低10.01%，应变降低10.07%。