轴向循环加载卸载条件下饱和软土变形特性试验研究

王学营， 岳夏冰， 惠 冰

(1.内蒙古自治区交通建设工程质量监督局， 内蒙古 呼和浩特 010020； 2.长安大学 公路学院， 陕西 西安 710064； 3.中交通力建设股份有限公司， 陕西 西安 710075)

1 研究背景

随着我国经济的快速发展，城市交通基础设施建设也相继迅速发展。高层超高层建筑、高速公路和铁路工程、桥梁隧道工程、地铁和越江隧道工程、地下商场、水电站、大型油罐等相继修建。而这些工程必然要穿越或修建在软土之上，并且经常承受着变载的作用，因而卸载作用随之可见。从大量的工程实际和试验研究表明，软黏土具有明显的流变性，软黏土变形和强度特性与其应力状态以及加载历史密切相关，岩土材料在外荷载下所产生的塑性变形是不可逆的。循环加卸载造成的变形将会不停累积并决定最终变形。

受应力历史影响，每经历一个加卸载，其再加荷所产生的变形将明显小于前次。这也是为什么同荷载下超固结土所产生的变形明显小于正常固结土的原因。

“加荷-卸荷-再加荷”这种加荷方式就是通过荷载的循环模拟土的应力历史。

与普通的单轴及三轴试验相比，加卸载试验更能揭示土的力学特征，因而研究循环加卸载条件下软黏土的强度和变形特性具有一定的工程实践价值[1-2]。目前关于循环荷载条件下岩土体变形特性的研究也比较多，但大多数是循环三轴试验，而在K0状态下一维固结轴向循环加卸载试验研究目前还较少[3-4]。

本文依托实体公路工程。由现场取样，通过利用长安大学自行研制的连续加载K0固结仪，对所取一定深度饱和土开展循环加卸载试验，分析其在整个试验过程的变形特征和在整个加卸载过程中土体弹、塑性变形与应力水平的关系，建立了相应的表达式，以便于工程实际应用。最后根据试验结果建立了循环加卸载本构方程[5-7]，并对塑性滞回能进行计算拟合。

2 循环加卸载试验

此次饱和软黏土循环加卸载试验采用长安大学自行研制的一维侧限固结仪。该试验仪器由三轴加荷装置进行加荷，由固结仪上的传感器观测试验过程中的轴向应力、侧向应力、轴向位移和孔隙水压力，并通过数据储存系统记录试验数据。

本试验土样采用武汉地区软土，呈灰色，软塑状态，有机质含量较多，试样为圆柱体状，尺寸为高40 mm、直径61.8 mm，塑限wp=31，液限wl=59，塑性指数IP=28。该试样采用真空饱和气进行饱和，具体饱和过程为：将制备好的试样放入饱和缸内，封盖前用凡士林进行密封，确认密封完好后开始抽真空。当真空压力表值达到0.01，打开连通饱和缸的水管，向其内注水，直至试样被水覆盖2～3 cm时，停止注水并继续保持抽气机抽气10～15 min，最后打开空气阀。静置24 h后即可。饱和后土样的饱和度Sr=99%，ρ=1.69 g/cm3，e0=1.44。试样饱和后进行循环加载卸载试验。饱和试样制备完以后将试样放入固结仪内，试验首先在完全侧限条件下对土样进行连续加载。先对试样施加1 kPa的预压力，并将测试传感器均归零。采用0.002 4 mm/min的加荷速率。对试样施加轴向应力，定时采集数据。当达到第1级应力水平后在同样速率下进行卸载。当轴向应力水平卸载为0后，再对土样实施第2级荷载，达到第2级应力水平后再次卸载，直至最后1级荷载。试验结束，关电源，拆除仪器，取出试样。试验共设5级等增量加载、卸载，如表1所示。利用位移传感器量测土样达到相应应力水平时的总应变以及轴向荷载卸载为0时土体的残余应变。

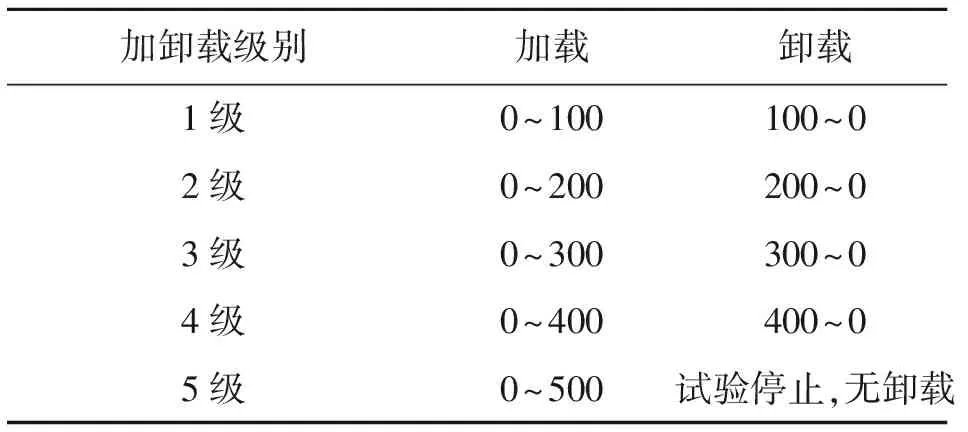
表1 循环加、卸载试验方案 kPa

3 加卸载试验数据分析及本构关系

3.1 试验数据分析

3.1.1 轴向应力与轴向应变关系图 本文以2级循环加卸载对轴向应力与轴向应变关系进行说明，如图1所示。图中L1为初始加载曲线，L2为卸载曲线，L3为再加载曲线，L4为第2级卸载曲线，4个曲线对应的初始变形模量分别为En1、Em1、En2、Em2、；卸载顶点为A(ε1，σ1)和B(ε2，σ2)，εp1、εp2为卸载过程轴向应力为零时所对应的应变，即为试样的塑性变形；σn1、σn2为加载阶段轴向应变趋于无穷大时对应的最大轴向应力；εm1、εm2为卸载曲线轴向应力趋于无穷大时的最大轴向应变。

由图1可以看出，试验加载过程体积减小，卸载曲线及加载曲线坡度均与加载曲线的起始坡度相等。在再加载曲线的最后阶段，即再加荷载超过前次卸载值后，其对应的曲线将保持原单轴加载曲线同一路径继续上升，相关学者定义为岩土材料的变形记忆[4]。在卸载和再加载曲线之间形成了一个封闭的滞回环，土体的应变既有不可恢复的塑性应变又有可以恢复的弹性应变。初始切线模量是由初始加载曲线计算所得，回弹模量则由卸载曲线确定，其均可用于沉降分析与计算。由图1可见，任一加卸载循环曲线，相等的应力增量所对应产生的应变增量不等，初始加载曲线所对应的应变增量值明显大于再加荷曲线，这也说明了土体的应力历史对变形是有影响的[5]。

3.1.2 卸载曲线分析 软土在K0状态下各级卸载曲线的轴向应力与轴向应变曲线如图2所示。

图2显示，各级卸载曲线的变化趋势是相同的，卸载初期曲线的变化趋势较陡，可近似为直线；而随着卸载时间不断增加，卸载为曲线形式。而卸载曲线主要是由曲线段构成的，这也说明了饱和软土的非线性特性，这是与岩石卸载曲线不同的。通过卸荷曲线可以求得饱和软土的变形模量以及土体的塑性变形。隧道围岩长期处于卸载环境中，通过得到K0状态下的卸载曲线，在建模计算时采用卸载曲线的变形模量更接近于实际工程。

3.1.3 再加载曲线分析 图3为饱和软土K0状态下循环再加载各阶段对应的轴向应力与应变曲线。由图3可见，各阶段曲线前期至上级卸载值均近似为衰减形曲线，各阶段曲线后段，即超过上级卸载值时，所有再加载曲线均近似为直线形，且均保持初始加载曲线同一路径上升。对于非饱和土或一般的地基土，其加卸载曲线与初始加载曲线的起始切线斜率大致相等，但本试验研究的为饱和软土，其所对应的两者间曲线斜率相别明显，此差异的产生是由于加卸载影响了饱和软土的物理力学特性所致，同时也表明饱和软土的弹性变形较小。一般用再加载曲线的切线斜率表示各级再加载的变形模量，以各级再加载曲线的变形模量的平均值描述再加载曲线的变形特征[3]。

在施工过程中，地基土处于加载卸载再加载状态，且当上覆压力小于地基土的初始应力时，为最大程度接近与实际工程，则在数值计算中，建议选用K0状态下再加载曲线的变形模量。

3.1.4 弹性应变与塑性应变变化规律分析 在饱和软土加卸载曲线上可以求得试样在各级卸载为零时的弹性变形和塑性应变，结合试验结果与理论分析，分别将弹性应变和塑性应变随各级卸载载荷的变化规律进行分析，如图4、5所示。

从图4、5可以看出，饱和软土在循环加卸载试验中试样的弹性应变与塑性应变都是随着卸荷等级的增大而增大的，但塑性应变的变化率高于弹性应变变化率，因次饱和软土具有一定的强度，且两者都与卸荷应力水平呈良好的线性关系，可用下列回归方程表示：

(1)

(2)

公式(1)、(2)分别表示该试样在一维K0状态下循环加卸载试验得到的弹性变形和塑性变形，对以后工程实际计算土的弹塑性变形时有一定的参考价值。

3.2 加卸载的本构关系

3.2.1 本构方程推导 在轴向循环加卸载应力-应变关系曲线中，通常取曲线上轴向力为0时所对应的切线斜率作为加载或卸载过程中试样的轴向初始变形模量Eni，用该模量确定双曲线方程，前一级加载曲线和卸载曲线确定下一级卸载曲线和再加载曲线的初始变形模量[6-9]，从而建立循环加卸载过程的本构方程。

根据试验结果(图1～5)可得，加载曲线L1方程用双曲线方程可表示为：

(3)

公式(3)也可用下式表示：

(4)

因此公式(3) 可以变为：

(5)

整个加载曲线L1的变形模量可以写为[6]：

(6)

卸载曲线L2的方程可以写为：

(7)

由于A点在卸载曲线上，将A点的坐标代入公式(7)可以得到：

(8)

卸载曲线轴向应力为零时对应的变形模量可通过试验求得：

(9)

卸载曲线上轴向应力趋于无穷大时的轴向应变可表示为：

(10)

将公式(9)、(10)代入公式(7)，可求出C和D：

C=Em1

(11)

(12)

将公式(11)、(12)代入公式(8)中整理后可得到方程式：

(13)

求解方程(13)可得到：

(14)

根据公式(14)可以求得卸载为零时试样的变形量，即试样的塑性应变。

将公式(11)、(12)代入公式(7)中，可以得到卸载曲线应力表达式：

(15)

卸载过程的变形模量可表示为：

(16)

根据同样方法可以求得再加载曲线L3的应力表达式以及变形模量表达式为：

(17)

(18)

根据上述方法可将饱和软土循环加卸载的应力-应变方程及变形模量表述出来：

初始加载曲线：

(19)

卸载曲线：

(20)

(21)

再加载曲线：

(22)

(23)

式中：i=1,2，…,n。

公式(19)～(23)即为饱和软土循环加卸载曲线的本构方程及变形模量的表达式，式中的Eni,Emi,εp(i-1),εmi,σni参数均可在常规固结仪中的循环加卸载试验中得到，通过施加的轴向应力可以算出所对应的某一时刻的轴向应变。

3.2.2 本构方程验证 上述公式(19)、(20)、(22)为饱和软土循环加卸载试验的本构方程，方程中的参数为Eni、Emi、εp(i-1)、εmi、σni，可通过常规循环加卸载试验得到，将这些参数整理如表2所示。

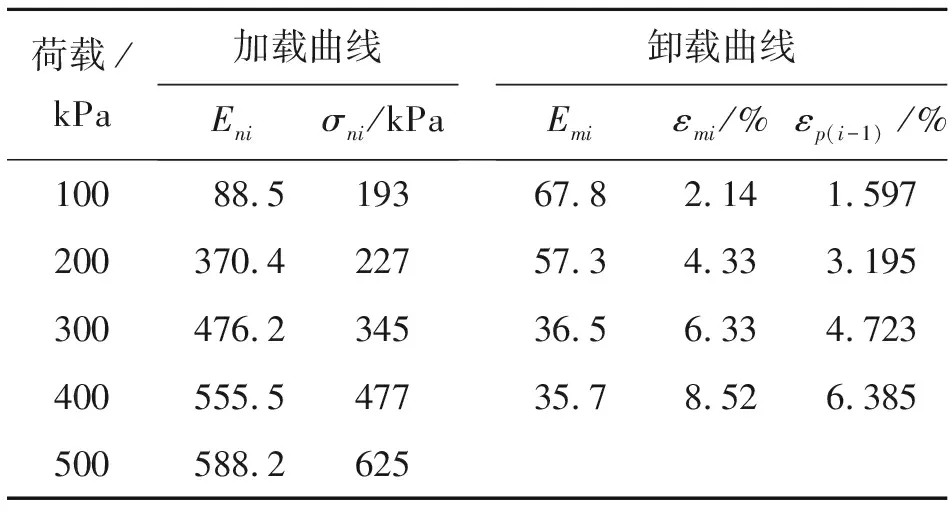
表2 本构方程各参数

将表2中的各参数代入公式(19)、(20)和(22)中，可求出循环加卸载任意轴向应力所对应的轴向应变，将本构方程计算结果与试验数据进行了对比分析，如图6所示。

从图6可以看出，本构方程计算的结果与试验结果虽然存在一定的差异，但总体的变化趋势是相同的，说明该本构方程能够用来描述饱和软土的循环加卸载特性。

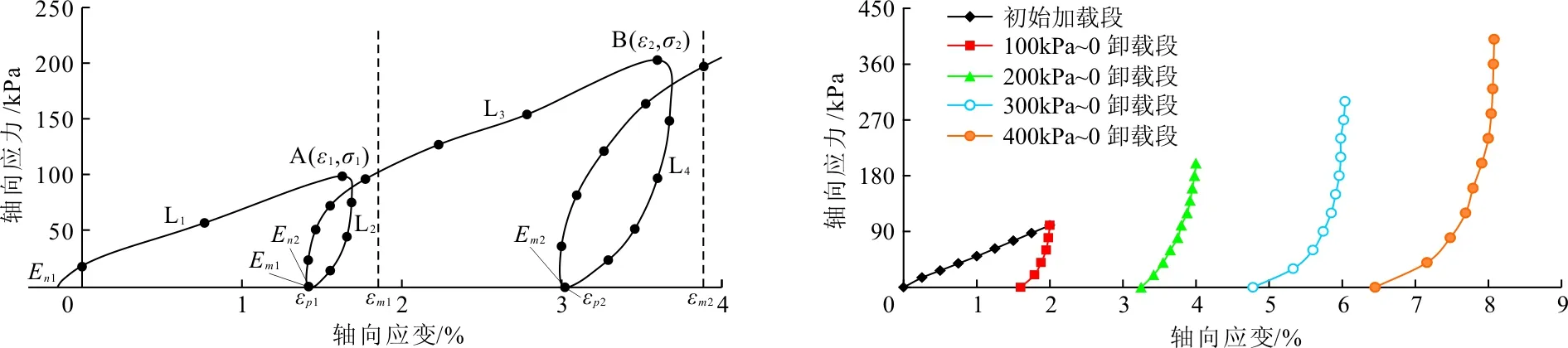
图1软土土样轴向应力与轴向应变关系 图2软土土样卸载曲线轴向应力与轴向应变曲线

图3软土土样再加载曲线轴向应力与轴向应变关系 图4软土土样弹性应变与卸载载荷关系

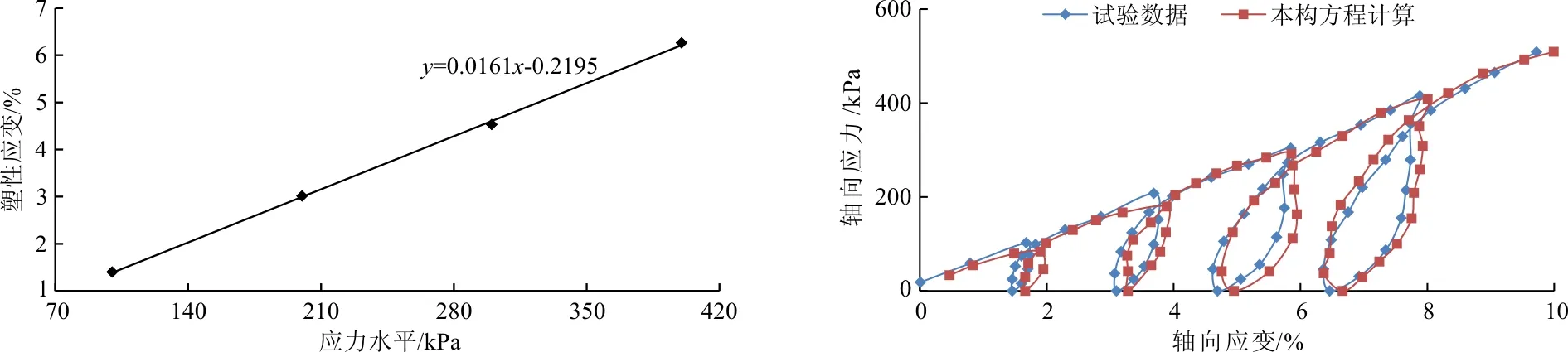
图5软土土样塑性应变与卸载载荷关系 图6本构方程计算结果与试验数据对比

3.3 塑性滞回环分析

饱和软土土样循环加卸载试验的塑性滞回环示意图见图7。从图7可以看出，饱和软土加卸载试验再加载曲线与卸载曲线并不重合，而是形成一个封闭的滞回环，这是由于饱和软土具有一定的塑性变形，且随着荷载等级越高，滞回环的面积越大，表明饱和软土的塑性越大[10]。用滞回环的面积表示饱和软土在加卸载过程中滞回能的大小[3]，而滞回能是描述加卸载过程中能量消耗的重要参数，本文就滞回能的变化规律进行如下分析。

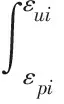
(24)

式中：Wi为每级卸载再加载过程中的滞回能；εpi为卸载为零时的应变；εui为卸载曲线与再加载曲线上交点所对应的应变；σli为滞回环上各级再加载曲线任意时刻的轴向应力；σui为滞回环上各级卸载曲线任意时刻的轴向应力。

将公式(20)、(22)代入公式(24)中计算滞回能如下：

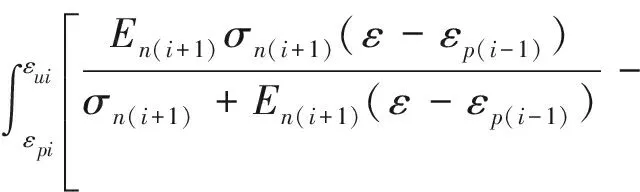
(25)

利用公式(25)计算滞回能见表3，并建立滞回能与卸载应力等级的关系。

表3 各级卸载应力水平下的滞回能

试样加载最大轴向应变εmax以及各级卸载为零时试样的轴向应变εpi可根据图7解出来，将表3中的参数代入公式(25)则可求出塑性滞回能的大小。从表3可以看出，随着荷载等级的不断增大，各级卸载曲线初始变形模量不断减小，而再加载曲线的初始变形模量则不断增大，各级滞回能也不断增大，这是由于随着试样循环荷载的增大，土体的塑性在不断增大。

本文对塑性滞回能与卸载应力水平的关系进行整理，得到了两者呈二次曲线关系，如图8示。

图7 饱和软土土样加卸载试验塑性滞回环示意图

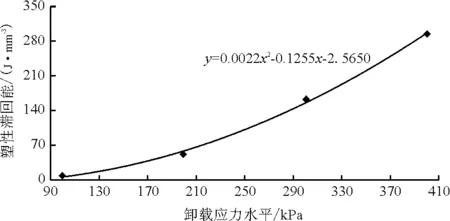
图8 塑性滞回能与卸载应力水平的关系

根据图8，可将塑性滞回能和卸载应力水平用下列回归方程表示：

(26)

式中：Wi为塑性滞回能，J/mm3；σi为各级卸载应力水平,kPa；A,B,C为回归系数。

4 结 论

本文通过对饱和软土开展轴向循环加卸载试验的数据进行分析，得出以下主要结论：

(1)各级卸载与再加载曲线的变化趋势是相同的，试样的变形表现出了非线性特性，卸载和再加载曲线主要有曲线段组成，当再加载曲线荷载超过上级卸载荷载时，曲线近似为一条直线，且沿着初始加载曲线上升。这些规律可通过对试验过程中的变形模量分析来加以验证；

(2)由于软土试样具有可塑性，所以在试验过程中试样的变形主要包括弹性变形和塑性变形两个部分，通过试验数据求得试验弹性变形和塑性变形，并且分析后，可知弹性变形和塑性变形均与卸荷应力水平呈线性关系；

(3)通过利用加卸载曲线的初始变形模量推导出了卸载和再加载两个过程的轴向应力与轴向应变的双曲线本构方程，并验证了其可靠性；

(4)通过对试验曲线的分析计算，得到试样加卸载过程中消耗的塑性滞回能与卸载应力水平呈良好的双曲线关系，且随着荷载等级增大而增大。