一种结合优化后AES与RSA算法的二维码加密算法
2019-11-26刘海峰梁星亮
刘海峰, 刘 洋, 梁星亮
(1.陕西科技大学 文理学院, 陕西 西安 710021; 2.陕西科技大学 电子信息与人工智能学院, 陕西 西安 710021)
0 引言
二维码作为一种存储、传递和识别信息的技术现已在多个领域得到了广泛的使用,例如物流、交通、电子商务等.但随着二维码在市面上的推广,二维码的信息泄露危险也日益突出.由于二维码的生成标准是公开的,且未能在编码过程中实现信息加密,攻击者可以通过二维码截获到存储和传递的信息,存在着一定安全问题[1].对于未加密的二维码,任何获得二维码的人进行扫描后均可得到二维码中保存的信息,这对涉及个人隐私敏感信息领域造成使用上的不便.例如在追溯系统中,产品信息生成的未加密的二维码在传输过程中,若被不法分子获得,便可进行假冒印刷等一系列违法行为,使用加密后的二维码作为保存、传递产品信息的媒介,可以起到规范市场,打击假冒的目的.对于二维码信息进行加密,既保证了它的隐私性,也为使用者的个人安全提供了保障.因此,有关二维码的加解密的研究成为一个热点问题.
目前,国内对于二维码信息安全的研究取得了一些初步进展.2014年,于英政等[2]提出结合了DES和RC4加密算法,选取DES和RC4两种算法之一,针对不同阶段的二维码信息进行加密,实现了对二维码分阶段加密;安吉旺等[3]提出对编码信息采用RSA和key口令的算法进行二维码混合加密,对明文信息分组加密后,通过key口令对分组明文加密,再使用RSA算法对key口令的密钥进行加密.在专用的识别软件上,如果输入正确的私钥可解密出相应的明文信息.2015年,肖本海等[4]基于SHA512和AES两种算法对二维码信息及其密钥进行了加密,提高了对密文的保护;同年,廖镇勋等[5]提出一种针对二维码的不同阶段,探究其差异并采用不同的方法进行二维码的加密,提高了二维码加密的程度.2017年,龙强等[6]提出一种基于非对称密码体制的二维码加密算法,该算法将非对称加密算法RSA与Logistic混沌模型相结合,对二维码中信息及密钥进行加密编码,保证了二维码中信息可以在不安全的信道中安全地传输.2018年,张华[7]探讨了利用非对称 加密算法加密二维码的可行性和安全性;葛娅敬等[8]提出对二维码图片矩阵进行奇异值分解从而加密得到密文,解密得到明文,使基于图像处理上的二维码信息安全有了一定进展.杨康等[9]针对不同的信息权限和属性集,生成访问控制树,通过不同用户的属性分配对应的不同私钥,实现了二维码的分级加密.
综上,当前针对二维码加密的方式分为对生成的二维码图像的加密和对未进行生成二维码之前的初始明文信息的加密.在对二维码信息加密的讨论中,主要是针对二维码加密算法安全性的讨论,使用RSA非对称算法为例的加密算法存在着加密或解密算法时间复杂度高的问题,而使用以DES对称算法为例的二维码加密算法,又存在着DES超期服役和密钥传输是否安全的问题.
本文提出一种结合改进的AES算法和RSA优化算法的二维码加密算法.本算法在生成二维码之前,对明文信息加密,利用AES对称密码算法加密效率快和RSA非对称算法便于密钥管理的优势,基于算法安全性的基础之上实现了对密钥的安全管理.同时通过对两种算法的优化减少加解密消耗的时间,实验证明,该算法提高了二维码加密的效率.
1 算法理论
1.1 二维码
二维码,又称二维条码或QR Code.在固定好的平面区域,二维码通过散落的黑白相间的图形按一定的规律排序,从而记录数据信息.QR码与传统一维条码相比:数据承载量更大;属于纠错编码;可以引入加密体系;编码范围更广.QR码的这些特性,决定了其作为载体,在信息时代会有更多的发展空间.
1.2 AES算法
AES算法是一种新型加密方法,具有更加可靠的加密过程和更加适合的密钥长度.AES算法包含三大部分:密钥扩展,加密和解密.密钥长度有128位、192位、256位3种.密钥扩展算法的输入是一个4字的密钥,输出是一个44字的一维线性数组.每轮的密钥由种子密钥经过扩展得到.128位的AES加解密算法由十轮组成(192位12轮,256位14轮),每一轮有四个基本步骤:ByteSub变换:用一个S盒完成分组中的按字节的代换,ShiftRow变换:一个置换过程,MixColumn变换:一个利用在GF(28)上的算术特性的代换,AddRoundKey变换:当前分组按位异或扩展密钥的一部分.解密算法和加密算法不同,仅仅密钥扩展形式一样,但对于加密解密中转换顺序是不同的.
1.3 AES算法改进
1.3.1 密钥扩展改进
在传统AES算法密钥扩展部分,使用初始输入的4字(16字节)的密钥进行密钥扩展后,得到44个字(156字节)组成的扩展密钥数组W=(w0,w1,…,w43).由输入的密钥可直接先得到W的前4个字:w0,w1,w2,w3,W剩余的字由前一字以及前面第四个字进行如下运算操作得到:当下标数字不为4的倍数时,直接进行异或操作,否则,先与前一字进行g变换,再和前第四字进行异或操作,如图1所示.这种密钥扩展算法面临的主要挑战是攻击者若是截取到其中一轮密钥,便可通过相应变换得到剩余所有密钥.

图1 传统AES算法密钥扩展过程
文献[10]提出一种密钥改进算法:在密钥扩展过程中,初始密钥不变,在密钥扩展过程中,使用与初始密钥无关的一套新密钥填充为第一轮扩展密钥,求解剩余密钥则继续使用AES密钥扩展算法依据新密钥扩展,最终得到全部密钥.算法原理如图2所示.

图2 改进AES算法密钥扩展过程
由于扩展密钥都是由新密钥通过AES算法扩展得到的,与初始密钥无关,因此扩展密钥和初始密钥不存在代数关系,对于攻击者来说,截取到任一轮扩展密钥也无法推出初始密钥,反之,截取到初始密钥也无法推出扩展密钥.设种子密钥长为kbit,采用穷尽密钥攻击平均复杂度约为2k-1,以10轮AES算法来说,密钥攻击者平均需尝试2127次可能的密钥,而改进后的密钥扩展算法使平均需尝试2225次可能的密钥,以目前的计算能力很难破解.因此该算法在保证与程序效率不变的基础上克服了程序被截取一轮密钥即可破解全部密钥的漏洞.
在这种密钥扩展改进算法中,若攻击者已知算法密钥扩展改进过程,又成功截取到初始密钥x0和其后由任一轮由新密钥或新密钥扩展得到的密钥,那么攻击者依然可根据密钥扩展过程由任一轮密钥穷尽推出新密钥,进而得到全部密钥.
面对这种挑战,本文提出一种在文献[10]密钥扩展算法上的改进算法:初始密钥不变,依照原始密钥扩展算法进行轮密钥扩展,增加随机轮数k(1 图3 本文AES算法密钥扩展过程 对于之前的攻击者,攻击分为以下情况: (1)攻击者截取到十轮中任两轮密钥,但未知随机轮数k情况下:①两轮密钥均由初始密钥或新密钥之一进行密钥扩展而来,由于开始选取的新密钥与初始密钥无关,则攻击者无法推得另一密钥及其扩展密钥,进而无法获得全部密钥;②两轮密钥分别由初始密钥和新密钥之一密钥扩展而来,则攻击者在未知捕获的两种密钥分别属于新密钥或初始密钥和未知分别属于两种密钥扩展的哪一轮密钥扩展情况下一共有90种可能的密钥组合,大大增加了破解难度. (2)若攻击者截取到随机数k和初始密钥的情况下,由于不知道新密钥,无法通过计算获得全部密钥. (3)若攻击者截取到随机数和新密钥,情况和(2)相似. 1.3.2 列混淆变换改进 在传统AES加密算法中,MixColumn变换即列混淆变换,分为正向列混淆变换和逆向列混淆变换,提供算法的扩散性.列混淆变换的正向列混淆变化对每列独立地进行操作.每列中每个字节被映射为新值.式(1)表示GF(28)上正向列混淆变换,用于数据加密,式(2)表示GF(28)上逆向列混淆变换,用于数据解密. (1) (2) 在AES算法中,加密过程中,列混淆变换需要执行4次xor加法和2次xtime乘法,而解密过程中逆列混淆变换需要执行9次xor加法运算和12次xtime乘法运算[10].加密算法和解密算法因列混淆算法不同,导致加解密耗时不对等,解密算法中需要更多的时间来进行运算. 文献[10]提供了最简单形式的正向列混淆运算矩阵和逆向列混淆运算矩阵. (3) 用M矩阵代替原AES算法中正向列混淆和逆向列混淆运算中矩阵,减少了逆向列混淆运算所消耗时间,使正向列混淆运算和逆向列混淆运算消耗相同的运算资源,均为执行4次xor加法和2次xtime乘法,解决了加解密耗时不对等问题. 本文对M矩阵进一步改为: (4) 这样改进M后,正向列混淆和逆向列混淆均减少执行2次xor加法运算,加密耗时和解密耗时的共同降低使运算速度得到一定提升,章节4.1中的表1 罗列了对同样数据量加密或解密所用时间的对比. RSA是典型的非对称加密算法,它的特点是使用两个密钥的密码算法,具有方便密钥管理和传送的特点.它的基础是大数分解的困难性,它的核心是模幂运算.主要包括两个方面:密钥的产生和加密解密. RSA密钥的生成过程: (1)首先选出两个大的素数p和q,要求p不能等于q,且p和q有一定的差距. (2)计算出n=p*q. (3)计算出Ф(n)=(p-1)*(q-1). (4)选择e,使得1 (5)计算解密密钥参数d时,要求ed=1 mod Ф(n),可用扩展的欧几里得算法求解.由此得出,私钥(d,n),然后公开n参数,其中n又被称为模,保密原始素数p和q. 其中(e,n)是公钥,(d,n)是私钥.d是秘密的,而n是公开的.密文的解密者(或系统)将公钥公开,而将密钥和系统参数两个大素数p、q藏起来. 对于RSA算法:D(E(M))=(Me)dmodn=(Md)emodn+E(D(M)),其中M为明文,加密公式C=E(M)=Memodn,解密公式M=D(C)=Cdmodn. 由于RSA算法中模正整数次幂的运算过程复杂,影响算法执行效率,是限制RSA发展的主要难题.而RSA算法的解密者拥有保密的系统参数p、q和私钥,可以在解密过程中利用中国剩余定理进行解密优化,先对中国剩余定理做简单介绍.对于同余方程组(5): (5) 若满足:①m1,m2,…,mr为两两互素的正整数;②a1,a2,…,ar为整数,则同余方程组(5)的模M=m1,m2,…,mr有唯一解(证明过程省略): (6) 其中:Mi=M/mi yiMi≡1 modmi,1≤i≤r 可见,中国剩余定理能够把高位宽大数的模幂运算转换为低位宽相对较小的模幂运算.下面叙述运用中国剩余定理改进RSA解密的方法[11]. 在RSA算法中,存在两个互素的数p、q,由中国剩余定理,可知求解密方程M=D(C)=Cdmodn的运算,等价于求同余方程组(7),由此,可实现由计算模n的数量级转化为计算模p和模q的数量级. (7) (费马小定理)p为素数,x为满足x(modp)≠0条件的整数,则:xp-1≡1(modp). 由费马小定理,令r=d(modp-1),则存在k满足:d=k(p-1)+r.故: M1=Cd(modp)≡Ck(p-1)+r(modp)≡ (C(p-1)modp)kCr(modp)≡ 1kCr(modp)≡Cd mod(p-1)(modp)≡ (Cmodp)d mod (p-1)(modp) 同理,对同余式M2=Cd(modq),有:M2=(Cmodq)d mod (q-1)(modq).令d1=dmod(p-1), d2=dmod(q-1).因此,同余方程组(7)转化为低指数的同余方程组(8). (8) 又由中国剩余定理和费马小定理可知其解: M=((Cmodp)d1q(q-1modp)+ (Cmodq)d2p(p-1modq))modn= ((Cmodp)d1q(qp-2modp)+ (Cmodq)d2p(pp-2modq)modn= ((Cmodp)d1q(qp-2modn)+ (Cmodq)d2p(pq-2modn)modn= ((Cmodp)d1(qp-1modn)+ (Cmodq)d2pq-1modn)modn 将中国剩余定理应用在RSA算法解密过程中,远远小于直接进行解密所需指数运算数量级,而且通过多项式运算代替逆元的求解,进一步减少运算时间,从而提高运算速度. 根据RSA的快速MMRC解密算法[12],步骤1-5为快速解密算法.运用这种算法共有1次逆元,2次乘法,1次加法,1次减法和1次k比特模余,RSA算法解密效率得到进一步提升.计算以下各式: (1)d1←d(modp-1)与d2←d(modq-1) (2)C1←C(modp)与C2←C(modq) (3)M1←C1d1(modp)与M2←C1d2(modq) (4)B←p-1(modp) (5)m←M1+[(M2-M1)*B(modq)]*p 方案总体思路:采用以改进后的AES算法为主、改进后的RSA算法为辅的加密算法,将改进后AES算法加密结果与改进后RSA算法加密结果结合作为QR码算法的输入,然后进行二维码编码.不妨设Alice是二维码的生成方和发送方,Bob是二维码的接收方和验证方,明文为M.算法主要分为以下步骤: (1)系统建立 发送方Alice选择AES算法参数随机密钥x0和第一轮密钥y0,系统利用RSA生成算法及Bob选择的RSA公钥K1=(e,n),系统生成私钥K2=(d,n),并反馈给Bob,将K1公开,将系统初始化系数传递给接收方Bob. (2)信息加密 Alice采用改进AES加密算法,选定参数N=(x0,y0,z0)对明文进行加密,即利用改进后的AES密钥扩展算法,得到AES算法全部密钥,再利用全部密钥进行AES加密算法得到密文M′.将参数信息N用RSA算法公钥K1进行加密生成N′. (3)生成二维码 Alice将明文密文M′和参数密文N′拼接在一起并进行一系列后续操作即数据分析、数据编码、纠错编码、构造最终信息、生成掩膜和格式与版本信息等,生成含有加密信息的二维码. (4)密文解密 接收方Bob收到二维码信息后,扫描并通过RSA算法的私钥K2进行解密得到二维码参数密文N,结合改进后AES解密算法进而得到明文信息M. 算法加密流程如图4所示,算法解密流程如图5所示. 图4 算法加密流程图 图5 算法解密流程图 算法实现基于PyCharm平台,编程语言为python.QR二维码的生成识别采用zxing解析库、PIL,pillow和qrCode库. Alice在线传输明文信息给接收方Bob.Alice作为二维码生成以及发送方,传输M=′iamgladtoseeyous′作为信息明文,进行测试运行.Alice选择随机密钥x0=2345678910111213,新密钥y0=1520251221521113,z0=2,加密之后密文M′=c059e873b5a60a9104ef499f961a320B,Bob选取RSA算法公钥后,由系统生成1024位密钥,RSA算法加密x0得到x0′,加密y0得到y0′,加密z0得到z0′,中间用′//′分隔.x0′=12906416898900598349674 359045029739702606540597,y0′=425420404286 176275383986137492130476820305389897,z0′=8,将M′和N′用′//′拼接后进行后续二维码编码. 如图6所示,接收方Bob扫描得到:由AES算法加密的密文M′,由RSA算法加密的AES算法初始向量与第一轮密钥密文N′.首先使用系统建立时的私钥K2进行RSA解密,得到参数明文(x0,y0,z0).再利用AES解密算法和参数N解密由二维码传递的密文M′,最终获得信息明文M= ′iamgladtoseeyous′. 图6 带有密文和参数密文信息的QR二维码图片 程序运行环境为:Windows 10,CPU2.5 GHz,RAM 4G.测试软件为PyCharm 2018.1.2.测试采用四种算法对二维码编码前明文加密: (1)文献[13]提出的AES算法. (2)文献[14]提出的3DES算法. (3)数据加密经典传输方案AES+RSA算法. (4)本文提出的结合了改进后的AES与RSA优化算法的加密算法.其中3DES使用3个56位的密钥进行加密.AES密钥长度均采用最广泛的128位,二维码存储明文字符串,四种算法对相同的48字节的字符串分别进行1000次加解密,取得加解密的平均时间,算法加密和解密时间测试结果在表1中列出. 表1 算法加解密时间比较 由表1可以看出,由于使用了RSA算法对AES密钥参数加密,结合AES和RSA的算法比仅使用AES算法耗费的时间长,但依然在加密速度上优于3DES算法,而采用综合改进后的AES和RSA优化算法加、解密消耗时间更少. 3DES算法是DES算法的一个安全变形,以DES为基本模块,通过组合分组方法设计出分组加密算法.目前,针对3DES算法的批评主要有: (1)3DES易受差分和线性密码分析攻击. (2) 3DES使用64位的块长度,不能满足大多数数据传输的要求. (3)用软件实现该算法的速度比较慢. 针对3DES的缺陷[15],AES算法得到了解决: (1)AES与3DES相比对差分、截断差分、线性、插值和平方攻击具有很强的抵抗力. (2)AES最小密钥长度为128 bits,最大密钥长度为256 bits,目前技术不存在穷举破解的可能.并且AES算法的密钥长度根据不同加密级别选择不同密钥长度,而分组长度同样可变,设计的灵活性高. (3) AES块长度128位,是3DES块长度的两倍 . (4)AES具有很高的加密效率. 3DES算法和AES算法两种对称密钥密码体制,密钥的分配均存在严重的缺陷,即若黑客在密钥传输过程中截取到密钥,则密文就不再保密.针对这一缺陷,RSA非对称密码体制使用两个独立的密钥,密钥的分配问题得到了解决. 本文提出一种结合了改进后的AES与RSA优化算法的QR加密算法.该算法结合两种算法优点,特别是对AES密钥扩展和列混淆变换两方面的改进实现了对明文的高效加密、通过RSA算法仅对参数信息加密,将明文信息加密后的信息密文和参数信息加密后的参数密文拼接生成二维码编码,再传送给接收方.在解密算法中,又对RSA解密算法使用中国剩余定理进行了优化.该算法相对于传统二维码传送信息和密钥而言,其加解密过程兼顾了效率和安全性,安全性能得到提高,加解密时间得到减少.该算法具有一定的推广和实用价值.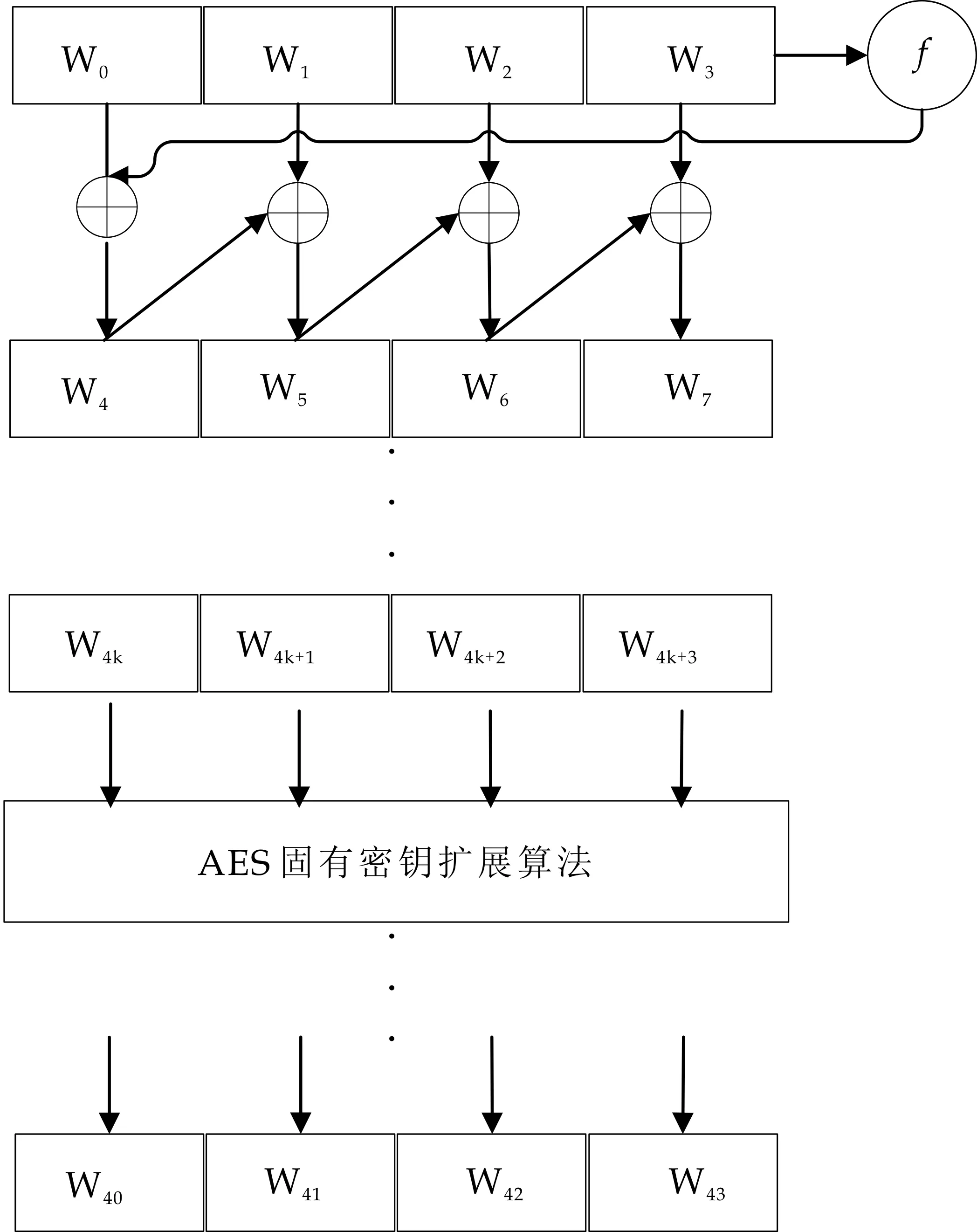
1.4 RSA算法
1.5 RSA算法优化
2 结合改进后AES和改进后RSA的QR加密算法
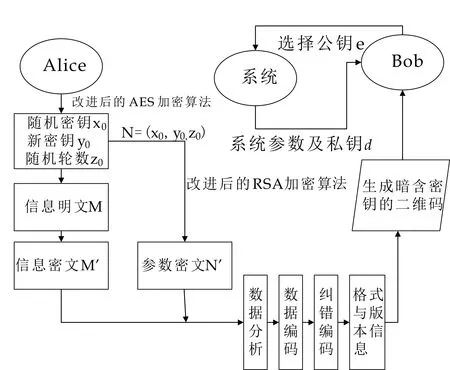

3 算法实现

4 算法测试
4.1 加密速度比较

4.2 安全性比较
5 结论
