永磁三自由度电机的运动学分析与动力学联合仿真

李争　刘令旗

摘 要：為了解决三维空间中多自由度电机传动精度较低、运动控制较差等问题，在刚性体机械系统下，基于复杂机械系统强耦合、非线性的特点，设计了一种可联动控制的三自由度电机。采用电机自转运动控制策略，分析了电机自转运行时的应力分布和形变程度，建立了混合驱动式电机的动力学模型，施加3个轴向转矩作为驱动力，规划了电机基于混合驱动式的三自由度运动，搭建并设计了机控一体化电机的动力学联合仿真接口。结果表明：通过激活有效阶模态，对刚柔耦合系统下的电机结构进行优化，可得到较小的偏心位移;多自由度电机的智能控制方案可自由设计被控对象的参数变化，降低了扰动的灵敏性，使控制系统具有较好的鲁棒性。结合三自由度电机的动力学数学模型来搭建基于滑模控制系统的联合仿真平台，可实现电机3个轴向角速度的轨迹跟踪，且在整个动力学联合仿真时段内均可实现跟踪效果，为后续实物样机的制造和测试提供了理论依据。

关键词：电机学;三自由度电机;偏心位移;虚拟样机技术;动力学模型;联合仿真接口;轨迹跟踪

中图分类号：TK172 文献标志码：A

doi：10.7535/hbkd.2019yx05003

Kinematics analysis and dynamics co-simulation of

permanent magnet three-DOF motor

LI Zheng， LIU Lingqi

（School of Electrical Engineering， Hebei University of Science and Technology， Shijiazhuang，Hebei 050018， China）

Abstract：In order to solve the problems of low precision and low motion control of multi-degree-of-freedom motor in three-dimensional space， under the rigid mechanical system， based on the characteristics of strong coupling and nonlinearity of complex mechanical systems， a three-degree-of-freedom motor capable of linkage control can be designed. The motor's rotation motion control strategy is used to analyze the stress distribution and deformation degree of the motor during the rotation. The dynamic model of the hybrid drive motor is established and three axial torques are applied as the driving force. The motor is based on the three-degree-of-freedom motion of hybrid drive， and the dynamic joint simulation interface of the machine-controlled integrated motor is built and designed. The results show that by activating the effective mode， the motor structure under the rigid-flexible coupling system can be optimized to obtain a small eccentric displacement. The intelligent control scheme of the multi-degree-of-freedom motor can freely design the parameter changes of the controlled object， reduce the sensitivity of the disturbance， and make the control system have better robustness. Combining the dynamic mathematical model of the three-degree-of-freedom motor to build a joint simulation platform based on the sliding mode control system， the trajectory tracking of the three axial angular velocities of the motor can be realized. The tracking effect can be achieved during the whole dynamics joint simulation period， which provides a theoretical basis for the subsequent manufacture and testing of the physical prototype.

Keywords：electrical engineering; three-degree-of-freedom motor; eccentric displacement; virtual prototype technology; dynamic model; joint simulation interface; trajectory tracking

随着智能化运动驱动装置的不断创新发展，可于狭小空间内实现多个自由度的运动受到人们的广泛关注。采用多台电机驱动需要依赖从动机构进行耦连控制，而由多自由度电动机作为主动机构直接驱动，可避免中间传动装置所带来的设备体积庞大、非线性耦合强、运动精度偏低等诸多不利因素[1-4]。球形电机因其特殊的结构可于三维空间内实现3个旋转自由度的运动。现有多自由度电机多为一个“整球体”的球型转子，通过对沿球面经、纬线排布的多组定子线圈施加不同幅值、相位的激励，实现三维空间内的多自由度运动。但此类电机难免存在体积庞大、转动惯量过大等问题，在单独实现高速旋转运行和定向倾斜操作时，易于产生较大的转子偏心位移，且难以输出恒定的转矩[5-10]。从国内外的参考文献中可以看出，关于多自由度电机的分析和研究大多侧重于本体结构的设计，而对电机三自由度的运动控制及轨迹规划却鲜有涉猎[11-14]。

在探究多自由度电机的动力学分析时，主要源于机械设计原理和经典理论力学的结合，但受电机做多自由度运动时快速响应的运动特性以及轴承摩擦、外部扰动等因素的影响，很难连续、稳定、精准地控制电机，常规的PID控制和转矩法控制往往无法满足轨迹跟踪精度的要求[14-17]。为此，基于复杂机械系统强耦合、非线性的特点，笔者提出了一种新型的适用于多自由度电机的智能控制方案[17-24]。

1 自转控制策略下的运动学分析

1.1 多刚体系统下电机的自转运行

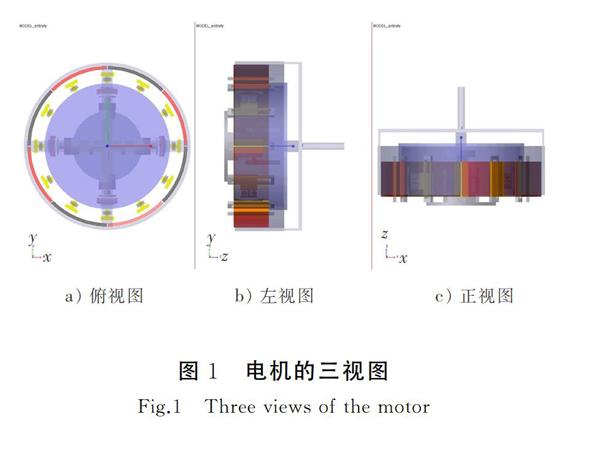
自转永磁体为8极结构，采用Halbach阵列充磁方式，永磁体磁路向内延伸;自转绕组采用单层分布式绕组，通三相工频交流电，产生旋转磁场与永磁体磁场相互作用，带动转子以同步转速自转。自转模块转子磁轭为偏转模块定子轭。偏转绕组为集中式绕组，在垂直于平面的方向上呈四列分布，偏转永磁体嵌于偏转转子轭上，与偏转绕组对应，给偏转绕组通直流电，产生N极或S极磁场，与转子永磁体对应的磁极相互作用，驱动转子永磁体绕关节轴承偏转，带动输出轴偏转。改变偏转绕组通电策略，可实现空间内的偏转运动[4]。混合驱动式电机的三视图如图1所示，包括俯视图、左视图、正视图，关于x-y角平分线的的轴测视图如图2所示。

电机的自转运行策略如图3所示，时域内的仿真时间为50 s，以角速度为参考量，设计电机加、减速阶段均为三次函数的抛物线式变化，对应角加速度曲线在相应时段内为二次函数的凸弧递增和凹弧递减，其加减速的时间均为10 s[7]。在中间时域内匀速旋转时达到最高转速，为31.4 rad/s，即达到电机高速运转时的300 r/s，角加速度在此时为0，而在电机启动与停转时刻达到最大值（10 rad/s2）。

1.2 刚柔耦合系统下的形变和应力分析

刚柔耦合系统中电机的自转运动采取与多刚体系统相同的控制策略，如图4所示，在仿真进行到中间转速最快的平稳匀速时段内，选取25 s处的时刻，运行仿真步数为250时，观测到电机形变程度最大，可见输出軸依据几何外形的特征被剖分为四棱柱体，显然添加的旋转副不再与十字型支撑连杆垂直，旋转副施加的关联点恰为电机输出轴始端圆环的中点。不难看出，支撑输出轴的十字连杆与输出轴交界部分的凹面棱角较为明显。电机自转模块运行时的形变程度主要来自所施加驱动的大小、方向和选取的一个位置点，故而靠近电机输出轴的十字连杆部分形变量较大，反之远离部分的形变量较小，而电机外壳和与电机外壳相连部分的连杆几乎没有形变。所以仅在此分析电机连接轴与转子轴的应力变化，如图5所示，最大应力值位于二者的交界部位，应力约为0.036 9 MPa，此后向四周均匀递减，最小应力值出现在连接轴一侧的中间部位，约为0.007 38 MPa。

对生成的柔性体进行编辑与模态优化，计算柔体时输入的模态阶数为6，定义旋转副的绞点有6个自由度，加上刚性体的6个模态，共需计算18阶模态。需要根据电机实际运行轨迹和控制策略，依据查看不同阶模态对电机输出轴、十字支撑连杆的位姿变化，考虑哪些阶模态对计算结果无法做出贡献后，使其失效，决定有哪些阶模态参与运动学和动力学的仿真计算。电机输出轴、十字支撑连杆的柔体形变大小，是依据构成模态的多个节点相对位移量的改变，再通过激活各阶模态的叠加后所得。因而在观测其各阶模态的当前位姿振型时，可调节形变比例因子至0.45，进而控制节点位移量的大小，将输出轴、十字支撑连杆的形变量调整到适度的位姿，以实现优化输出轴回转精度、减小偏心位移的目的[8]。

在选择电机输出轴、十字支撑连杆柔体的有效阶模态时，首先要保证输出轴具有一定的刚度和强度，其形变量尽可能小，以动画播放的形式观察各阶模态振型，并设置模态过滤，将该阶模态中最大位移点的量值小于设定值的模态都滤掉。确定激活柔体的第7阶、8阶、12阶、13阶作为有效阶模态，参与电机自转模块的运动学仿真计算，如图6所示。

研究电机自转时的偏心问题，采用先前相同的控制策略，以柔性体的关节点为物理量，对绕z轴旋转时在x分量、y分量上的偏心位移进行计算，如图7和图8所示。显然，在电机匀速运转阶段内偏心量的变化速度快，偏心位移的量值却很小;而在加速和减速过程中，偏心量的变化速度则相对缓慢，但其位移值相比较大。

首先从图7中x分量的旋转偏心位移变化可以看出，电机自转时启动0→5 s内偏心位移振幅呈现明显的衰减趋势，而在制动的45→50 s呈现明显的增幅趋势，且在启动的最初与制动的最末时刻，其振幅达到最大，为0.15 mm;在5→8 s的振幅衰减相较之前微弱一些，此后在8→10 s和40→42 s的2个过渡时期几乎与中间平稳运行时段曲线相似，仅在偏离0刻度的位置小范围波动。观察图8中y分量的旋转偏心位移，基本与x分量偏心位移曲线类似。在匀速平稳运行的前半段与启动至匀速的过渡阶段观测到有较小的衰减位移，在匀速平稳运行的后半段与匀速至制动的过渡阶段观测到有较小的增幅位移。通过对比不难看出，匀速时段内的位移量、波动率较小，在加减速时段内的位移量、波动率较大，2个分量的偏心位移均大致呈现对称的趋势，由此体现出了规划电机自转控制策略与电机结构设计的合理性。

2 混合驱动式电机动力学模型

为了更好地描绘电机的多自由度运动，取多刚体仿真软件中的系统全局坐标系为静态坐标系Oxyz，取电机转子轴标记点的局部坐标系为动态坐标系Odpq，引入欧拉角旋转序列的理论力学观念，即在静态坐标系下，转子轴由静平衡位置处经3次旋转后，形成新的确定位形，以章动角α、进动角β、旋进角γ为一组独立的运动参量，完成电机俯仰、偏航、滚动的三自由度运动[10]。

默认电机转子轴在静平衡位置处的动、静态坐标系重合，采用313的旋转序列，将绕坐标轴的由xyz相对运动到x″y″z″视为动态坐标系Odpq。分别给出3次旋转的坐标公式：

联立式（1）、式（2）、式（3）中3次旋转的坐标公式，得到由静态坐标系Oxyz向动态坐标系Odpq的转换公式和过渡矩阵，如式（4）所示。

为确切表征电机转子轴的位姿变化与外部施加3个方向转矩的关系，将所有转子部分视为同一个联动的刚性体，依据拉格朗日力学的第二类方程推导如下：

式（5）中：E为局部动态坐标系的的动能; qj为动态坐标系下第j个作用点; Qj为作用点qj下施加的旋转力矩。

电机在3个驱动转矩作用下运动到任一位姿时，均有与之相对应欧拉参量的转动坐标（α，β，γ）T，以向量形式表征电机转子轴沿轴线上的旋转角速度为w=（wx，wy，wz）T，依据动态坐标系向静态坐标系的转换关系，设定

为转动坐标（α，β，γ）T下的角速度，则动力学计算时的旋转角速度可由转动坐标下的过渡矩阵来表示[11-14]：

w1w2w3=

单以电机的三自由度运动而言，需满足机械系统自由度大于约束驱动数值的条件，有3个未被约束的自由度，即

n=3。广义局部坐标点q1=α，q2=β，q3=γ，广义驱动转矩Q1=τα-τfα，Q2=τβ-τfβ，Q3=τδ-τfδ。其中，τα，τβ，τδ表征电机转子轴受到内部载荷的影响，减速制动时段内驱动转矩在3个轴向分量上的幅值。

取笛卡尔全局坐标系为静止坐标系，则混合驱动式电机的自转部分和偏转部分同步推进时的动能为

为电机转子部分的惯性张量矩阵，用以反映电机刚体系统中内、外转子旋转状态下的惯性。

电机做多自由度运动时，在相对静态坐标系下沿不同轴线的旋转有所不同，故需确定说明其相对运动的轴。其中Jd，Jp和Jq为该永磁三自由度电机在局部运动坐标系dpq下，分别对于x轴、y轴、z轴的主轴转动惯量，其余惯性积均为0，且由于电机整体模型关于xoz和yoz两个坐标面对称，则Jd=Jp≠Jq[14]。此处令Jd=Jp=Jdp，上述动能表达式整合后如式（8）所示：

求解多自由度电机的动力学数学模型，主要是为了更好地描绘施加在电机3个方向上的驱动转矩与自转、偏转模块中各部件的位姿变化，建立混合驱动式电机在空间内三自由度动力学仿真的数学模型，如式（10）所示：

为其转子输出轴的惯性矩阵;[WTHX]τ为合分量转矩的矩陣;[WTHX]C（q，[AKq·]）=

求解所建立的动力学方程后，即得转子输出轴惯性矩阵的各个分量，如式（11）所示：

科氏离心力矩阵的各个分量如式（12）所示：

3 基于混合驱动式电机协同控制下的动力学联合仿真

在电机整体内部球面轴承与穿孔轴套的交界处添加球铰链，并施加3个方向的旋转力矩，作为驱动电机三自由度运动的转矩，其余内、外转子均以固定副相连，视为一个联动体，随输出轴运动而运动，通过给定不同形式的驱动转矩，即可使混合驱动式电机围绕其静平衡点做各式各样的三自由度运动。基于三自由度运动的球铰链中，约束3个滑移自由度，施加3个铅直坐标面的轴向转矩，继而实现电机的三自由度动力学仿真。

为体现电机在自转模块与偏转模块协同下的联动控制，规划一种在动力学下典型的三自由度运动工况轨迹，同时实现围绕z轴向左右两侧的摇摆运动和偏离z轴的倾斜运动，其合成为往复3次的闪电型运动。如图9所示，设定仿真时间为24 s，仿真步数为1 500，以嵌套式IF函数给定3个轴向转矩，控制绕x轴与绕z轴的驱动转矩为等幅的正余弦变化，相位差为90°，继而驱动电机完成每次往复运动的弧线偏移;控制绕y轴转矩为周期性的正弦变化，其中每8 s为一个周期，每个周期内间隔2 s进行分割，其转矩方向分别按照“+--+”的顺序循环3次，完成电机绕y轴往复3次运动的闪电型轨迹。

如图10所示，在上述3个轴向驱动转矩的合力作用下，即可实现电机的闪电型运动轨迹，可用于异性复杂机械零件加工，走出单自由度电机不能实现有特殊要求的复杂路径，譬如异形玻璃构件有玻璃钢丝缠绕时可有效躲避障碍物;同时实时测量3个轴向夹角，通过调试电机转动惯量、驱动转矩的大小与质心点位置，控制电机做闪电型运动时与x轴和y轴的轴向夹角为20°，与z轴的轴向夹角限制为25°[18]。

基于虚拟样机技术与控制系统流程进行协同控制，建立动力学联合仿真的接口模块，创建6个状态变量，设定3个轴向驱动转矩为输入变量，3个轴向角速度为输出变量，并与电机模型对应的外部载荷产生电气关联。确定3个输入/输出接口，以机械系统子模块的形式导出，生成混合驱动式电机的虚拟样机模型adams_sub。如图11所示。设定为离散、交互式的运行模式，将电机的3个轴向驱动转矩作为输入函数，通过作为被控对象的虚拟样机模型adams_sub，得到电机的3个轴向角速度，完成动力学开环控制仿真。同时将电机的3个轴向角速度作为同步仿真数据存储至3个特定的工作空间，便于实现电机后续的轨迹跟踪控制[19]。

面对可能存在的输入扰动、轴承摩擦、参数摄动的不定性系统因素，选取拥有不变性、可靠性高、鲁棒性好的滑模变结构控制算法，与混合驱动式电机的动力学数学模型相结合，实现协同控制下虚拟样机与控制系统的实时数据交换。建立机控一体的联合控制仿真平台，通过编写S-Function完成电机的控制器算法设计。以混合驱动式电机的虚拟样机模型作为被控对象，将此前开环控制得到的3个轴向角速度作为联合仿真的3个输入量，同时将虚拟样机模型的3个轴向角速度输出量反馈至输入端，同样作为联合仿真的3个输入量。图12为滑模控制系统框图。

混合驱动式电机的动力学数学模型如下：

式中ε为虚拟样机模型做多自由度运动逼近滑膜面s=0时的快慢程度。ε的取值大小直接影响电机运动轨迹中任意一点到达滑模面的速率。若ε取值过大，则相应产生的“抖振”也越大。

经整理后可得动力学联合仿真的控制律为

基于混合驱动式电机的虚拟样机在实现自转运动与偏转运动的协同控制时，很可能出现较大的偏心位移与轴承摩擦等不定性因素，为进一步削弱抖振对滑膜控制系统稳定性的损害，使用饱和函数sat（s）替代控制器中的符号函数sgn（s），在边界层内部采用线性反馈，可于切换面附近形成平滑的趋近效果[20]。

图13中的a），b），c）分别对应x轴、y轴、z轴的角速度曲线，实线为混合驱动式电机的角速度/时间曲线，虚线为其跟踪曲线，z轴的输出响应于2.5 s后即可完全跟踪输入信号，而x轴与y轴的角速度输出响应则需在4 s后才能实现完全跟踪。相比之下，y轴的角速度跟踪于运动初始时误差较大，约为10 °/s，此后0.5 s才可体现跟踪效果，x轴与z轴的角速度跟踪于运动初时误差较小，分别约为0.5 °/s与1 °/s，在整个动力学仿真时段内均可实现跟踪效果。

4 结 论

1）依据电机实际运动状况，制定了自转运动的控制策略，选择通过激活有效阶模态对刚柔耦合系统下的电机结构进行优化，得到了较小的偏心位移。

2）在球铰链的约束下，规划了电机在空间内的三自由度运动，检测了与3个轴角度值的变化范围以及位移变化趋势，印证了实现电机三自由度运动的合理性与实用性，为后续实物样机的制造和测试提供了更多理论依据。

3）结合三自由度电机的动力学数学模型搭建基于滑模控制系统的联合仿真平台，可实现电机3个轴向角速度的轨迹跟踪。

4）本研究仅对三自由度电机在空载状态下一种典型运动工况进行了动力学联合仿真分析，并未实际考虑摩擦影响与带载情况，控制系统也仅为单闭环角速度积分反馈的滑模控制。因此，实现电机多自由度运动的滑模控制算法还有待进一步研究和完善。今后研究可选择合适的带载状态，基于球面轴承下点接触的摩擦系数进行测定，采用对角速度和角位置的双闭环积分滑模控制，实现对电机输出轴期望轨迹与响应速度的一并跟踪。

参考文献/References：

[1]HALL C E， YAO Z，CHOI M，et al.Progressive motor neuron pathology and the role of astrocytes in a human stem cell model of VCP-related ALS[J].Cell Reports，2017，19（9）：1739-1749.

[2]GMYREK Z，LEFIK M.Influence of geometry and assembly processes on the building factor of the stator core of the synchronous reluctance motor[J].IEEE Transactions on Industrial Electronics，2017，64（3）：2443-2450.

[3]ZHOU Huawei，ZHAO Wenxiang，LIU Guohai，et al.Remedial field-oriented control of five-phase fault-tolerant permanent-magnet motor by using reduced-order transformation matrices[J].IEEE Transactions on Industrial Electronics，2017，64（1）：169-178.

[4]  胡斌，陶征，劉旭.多自由度超声电机构建腕关节结构关键问题的研究[J].机械设计与制造，2017（11）：1-4.

HU Bin，TAO Zheng，LIU Xu.Study on key issues exsisted in the construction of the wrist joint structure based on the ultrasonic motor with MDOF[J]. Mechanery Design & Manufacture，2017（11）：1-4.

[5]  邱枫，杨臻，韩晓明.用于高转速球形电机的球形转子变形分析[J].机械设计， 2017（11）：38-41.

QIU Feng，YANG Zhen，HAN Xiaoming.Analysis of spherical rotor deformation for high speed spherical motors[J].Journal of Mechanine Design，2017（11）： 38-41.

[6]  胡波，王安东，李周斌，等.一种基于新型4-UPS+PSPR并联机构的动感座椅运动学和动力学分析[J].燕山大学学报，2018，42（1）：11-21.

HU Bo，WANG Andong，LI Zhoubin，et al.Analysis of kinematics and dynamics of a dynamic seat based on 4-UPS + PSPR parallel manipulator[J].Journal of Yanshan University，2018，42（1）：11-21.

[7] 韩善凯，李欣业，侯书军，等.钻杆纵-扭耦合振动两自由度模型的动力学分析[J].燕山大学学报， 2017， 41（3）：240-245.

HAN Shankai，LI Xinye，HOU Shujun，et al.Dynamics analysis of couple axial-torsional vibrations of drill-strings with two degrees of freedom[J].Journal of Yanshan University，2017，41（3）：240-245.

[8]  史婷娜，辛雄，夏长亮.采用虚拟电机的改进偏差耦合多电机同步控制[J].中国电机工程学报， 2017， 37（23）：7004-7013.

SHI Tingna，XIN Xiong，XIA Changliang.Multi-motor speed synchronous control based on improved relative coupling structure with a virtual motor[J]. Proceedings of the CSEE，2017，37（23）：7004-7013.

[9]  李富娟，李仕华，王凯，等.基于广义雅可比矩阵的空间并联机器人运动学研究[J].燕山大学学报，2018，42（4）：296-302.

LI Fujuan，LI Shihua，WANG Kai，et al.Kinematics analysis of space parallel robot based on generalized Jacobian matrix[J].Journal of Yanshan University， 2018，42（4）：296-302.

[10]李睿，吴凤英，张登权，等.三自由度永磁球形电机轨迹规划仿真[J].计算机仿真，2018，35（4）：342-347.

LI Rui，WU Fengying，ZHANG Dengquan，et al.Trajectory planning simulation of 3-DOF PM spherical motor[J].Computer Simulation，2018， 35（4）：342-347.

[11] 薛增涛，郭颖颖，李争.基于改进型滑模观测器的电动汽车用永磁同步电机转子位置估算[J].电机与控制应用， 2017，44（1）：1-5.

XUE Zengtao，GUO Yingying，LI Zheng.Estimation of permanent magnet synchronous motor rotor position for electric vehicle based on improved sliding mode observer[J].Electric Machines & Control Application，2017，44（1）：1-5.

[12]DOBZHANSKYI O，GOUWS R.Performance analysis of a permanent magnet transverse flux generator with double coil[J].IEEE Transactions on Magnetics，2015，52（1）：1-11.

[13]LI Hongfeng，LI Tianmeng.End-effect magnetic field analysis of the halbach array permanent magnet spherical motor[J].IEEE Transactions on Magnetics，2018，54（4）：1-9.

[14] 李争，邢殿辉，乜玮，等.永磁转子偏转式三自由度电机热特性分析[J].河北科技大学学报，2015，36（3）：279-285.

LI Zheng，XING Dianhui，NIE Wei，et al.Thermal characteristics analysis of a novel 3-DOF deflection type PM motor[J].Journal of Hebei University of Science and Technology，2015，36（3）：279-285.

[15] 张建华，李杨，吴学礼，等.基于U模型的非线性系统Super-Twisting滑模控制研究[J].河北科技大学学报，2016，37（4）：377-382.

ZHANG Jianhua，LI Yang，WU Xueli，et al.Study of Super-Twisting sliding mode control for U model based nonlinear system[J].Journal of Hebei University of Science and Technology，2016，37（4）：377-382.

[16]WESSEL J R，ARON A R.On the globality of motor suppression：unexpected events and their influence on behavior and cognition[J].Neuron，2017， 93（2）：259-280.

[17]夏長亮，李洪凤，宋鹏，等.基于Halbach 阵列的永磁球形电动机磁场[J].电工技术学报，2007，22（7）：126-130.

XIA Changliang，LI Hongfeng，SONG Peng，et al.Magnetic field model of a PM spherical motor based on halbach array[J]. Transactions of China Electrotechnical Society， 2007，22（7）：126-130.

[18]王群京，陈军，姜卫东，等.一种新型混合励磁爪极发电机的建模和计算[J].中国电机工程学报，2003，23（2）：67-70.

WANG Qunjing，CHAN Jun，JIANG Weidong，et al.The modeling and calculating on a new type hybrid Claw-Pole alternator[J].Proceedings of the CSEE，2003，23（2）：67-70.

[19] 李争，郭智虎，张玥.新型永磁转子偏转式三自由度电机磁场特性分析[J].河北科技大学学报，2012，33（5）：422-428.

LI Zheng，GUO Zhihu，ZHANG Yue.Magnetic field analysis of a novel 3-DOF deflection type PM motor[J].Journal of Hebei University of Science and Technology，2012，33（5）：422-428.

[20] 李争，刘朝英，宋雪玲.基于神经网络的无刷直流电机故障诊断和容错控制方法的研究[J].河北工业科技，2009，26（5）：411-414.

LI Zheng，LIU Chaoying，SONG Xueling.Study on fault diagnosis and fault tolerant control of BLDC motor based on neural networks[J].Hebei Journal of Industrial Science and Technology，2009，26（5）：411-414.

[21]MASMOUDI A，MASMOUDI A.3-D analytical model with the end effect dedicated to the prediction of PM eddy-current loss in FSPMMs[J].IEEE Transactions on Magnetics，2015，51（4）：1-11.

[22] 颜文旭，宁金，孙强，等.一种新型欠驱动型并联机器人的运动学分析与仿真[J].河北科技大学学报，2017，38（2）：190-195.

YAN Wenxu，NING Jin，SUN Qiang，et al.Kinematics analysis and simulation of a new underactuated parallel robot[J].Journal of Hebei University of Science and Technology，2017，38（2）：190-195.

[23] 王永婧，张冬雯，于健骐.基于T-S模型的一类时滞非线性系统模型预测控制[J].河北工业科技，2018，35（1）：37-42.

WANG Yongjing，ZHANG Dongwen，YU Jianqi.Model predictive control for a class of nonlinear systems with time-delay based on T-S model[J].

Hebei Journal of Industrial Science and Technology，2018，35（1）：37-42.

[24] 戴建國，赵志国，刘台凤，等.AFPM型轮毂驱动电机研究综述[J].河北科技大学学报，2018，39（1）：17-23.

DAI Jianguo，ZHAO Zhiguo，LIU Taifeng，et al.Review of AFPM hub motor[J].Journal of Hebei University of Science and Technology，2018，39（1）：17-23.