一题多解——直线与圆相交时的有关垂直问题

朱树家 徐加华

(山东省新泰市第一中学 271200)

直线与圆相交时的有关垂直问题，涉及问题形式较多，方法比较灵活，方法的选择尤为重要，方法选择得当，则会节省解题时间，从而提高解题速度.现举例加以说明.

例1已知方程x2+y2-2x-4y+m=0.

(1)若此方程表示圆，求m的取值范围；

(2)若(1)中的圆与直线x+2y-4=0相交于M,N两点，且OM⊥ON(O为坐标原点)，求m的值.

解(1)由题意得4+16-4m>0.解得m<5.

(2)方法一(圆系方程)

设过M,N两点的圆的方程为x2+y2-2x-4y+m+λ(x+2y-4)=0,

即x2+y2+(λ-2)x+(2λ-4)y+m-4λ=0,

故(λ-2)2+(2λ-4)2-4(m-4λ)>0. ①

说明：本法借助于圆系方程，由OM⊥ON知O在以MN为直径的圆上，利用过M,N两点的圆系方程，其圆心在已知直线上且过原点来构造含有m的方程组进行求解.

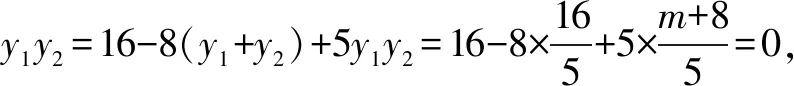
说明：本法借助于数量积的运算，把垂直关系转化为数量积的坐标运算，进一步把坐标的关系转化为方程的根的关系，从而借助于韦达定理来构造含有m的方程，来求得m的取值.

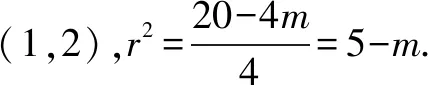
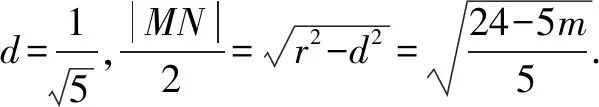
说明：本法借助于圆的弦长公式，以及直角三角形斜边上的中线等于斜边的一半来求解.

变式：若此圆圆心为C，且CM⊥CN，求m的值.

解析方法一(圆系方程)

设过M、N两点的圆的方程为：x2+y2-2x-4y+m+λ(x+2y-4)=0，

即x2+y2+(λ-2)x+(2λ-4)y+m-4λ=0，

故(λ-2)2+(2λ-4)2-4(m-4λ)>0。 ②

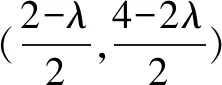
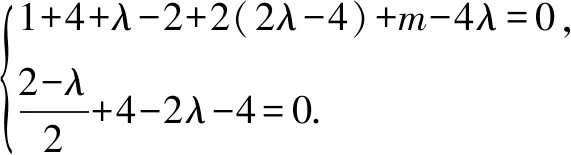
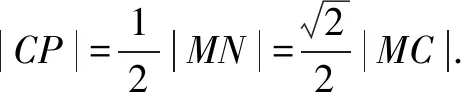
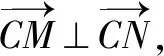
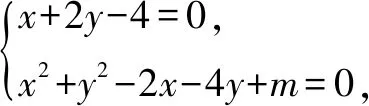
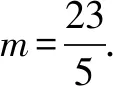
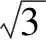
(1)求曲线E的方程；

(2)已知m≠0,设直线l1:x-my-1=0交曲线E于A、C两点，直线l2:mx+y-m=0交曲线E于B、D两点，若CD的斜率为-1时，求直线CD的方程.

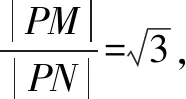
得(x+1)2+y2=3((x+1)2+y2),

化简得(x-2)2+y2=3.

(2)由题意知l1,l2均过定点P(1,0)，且l1⊥l2，故直线CD与圆E相交，且PC⊥PD.

以下用两种方法求解

方法一(代数法) 设直线CD方程为y=-x+b.

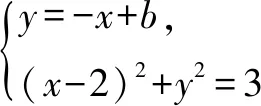
Δ=-4b2+24>0,b2<6.

=b2-3b=0,得b=0或b=3.满足b2<6.

故直线的方程为y=-x或y=-x+3，即x+y=0或x+y-3=0.

方法二(圆系方程) 设直线方程为x+y+b=0.

过CD的圆的方程为

x2-4x+y2+1+λ(x+y+b)=0，

即x2+y2+(λ-4)x+λy+λb+1=0，

(λ-4)2+λ2-4(λb+1)>0.③

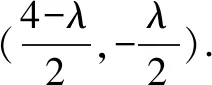
易知：以CD为直径的圆过P(1,0)，且圆心在直线x+y+b=0上.

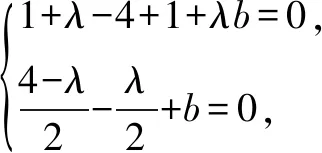
说明：本题若采用几何法，计算相对来说复杂一些，在此不再赘述.本题的关键在于看出l1,l2均过定点P(1,0)，且l1⊥l2.

本文通过三个例题列举了直线与圆相交时有关垂直问题的三种解法，通过解答，读者不难看出各解法的优劣.由此可见方法选择得当，会避免一些复杂的计算，提高解题速度，在考试中也会为其它题目争取更多的解题时间.当然，方法的选择还需要靠平时的积累，希望在此能起到抛砖引玉的作用.