圆锥曲线离心率全“求”通

谢慧芬

(江西省赣州市赣县第三中学 341100)

由于离心率涉及圆锥曲线较多的基本量、方程与曲线问题等，所以相对比较复杂，学生常常感到难以下手，不好把握，求解时也经常出错．下面就通过高考题和模拟题的分析、求解，总结出几种常见求法，大凡求椭圆离心率问题，用这些方法都能“求”通．

一、通过定义法求解

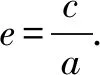
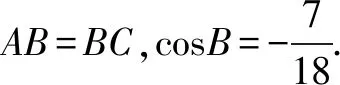
分析先设出AB的长，可知AB就是椭圆的焦距，然后用它表示出三角形其余的两边，再依据椭圆定义求出椭圆的长轴长，即可利用离心率定义求得椭圆的离心率．

解析设AB=2c，因为AB=BC，所以BC=2c.

由余弦定理得

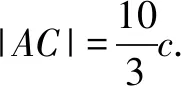
点评利用椭圆离心率的定义求离心率，关键是求出焦距(也就是半焦距)和长轴长(也就是长半轴长)，而求长轴长时，往往结合椭圆的定义．

二、借助方程法求解

例2 (广东卷)若一个椭圆长轴的长度、短轴的长度和焦距成等差数列，则该椭圆的离心率是( ).

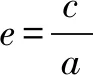
解析设长轴长为2a，短轴长为2b，焦距为2c，

由题意，2a+2c=2×2b，∴a+c=2b，

即(a+c)2=4b2=4(a2-c2)，

整理得5c2+2ac-3a2=0，即5e2+2e-3=0，

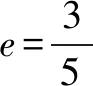
故选B．

点评方程法常用于已知或可以得到a,b,c，的关系式来求离心率的问题，解答的关键是把a，b，c的关系式转化为关于e的方程．

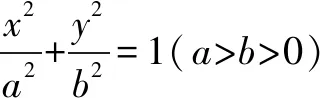
分析已知A,B的坐标，可以求出AB中点C的坐标，再代入椭圆方程即可得到关于a,b,c的方程，进而求得离心率．

点评已知点的坐标和点在椭圆上，自然而然地想到用代入法，直接建立起参数的方程关系，轻松求解，

三、采用几何法求解

求与过焦点的三角形有关的离心率，根据平面几何性质，再根据椭圆的几何性质以及定义，建立起参数之间的关系．通常画出图形，观察线段之间的关系，使问题更形象、直观，简单明了．

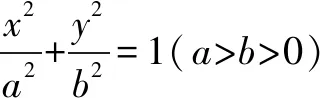
分析椭圆的一个短轴端点、焦点和坐标原点构成一个直角三角形，可在这个三角形中，利用三角函数求椭圆离心率．

因为∠F1BF2=120°，所以∠OBF1=60°.

故选B．

点评解答中所构造的△BOF1的三边长分别为椭圆的三个参数a,b,c，我们可以把这个三角形叫做椭圆的特征三角形，此时椭圆的离心率e=sin∠OBF1=cos∠OF1B．

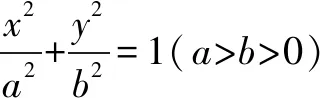
分析因为BF⊥x轴，所以我们可以由左焦点F，右顶点A以及点B三个点构造一个直角三角形，可以在这个三角形中，运用几何关系求椭圆离心率．

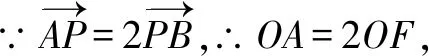
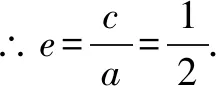
点评本题是对解析几何与平面向量结合的考查，既体现了几何与向量的交汇，也体现了数形结合的巧妙应用．先构造直角三角形，然后直接由三角形中边的比列关系得出a,c关系，简捷、迅速.

数学中的求值问题，主要有两种方法，一是代入(解析式、公式等)求值；二是解方程求值．求圆锥曲线的离心率也不例外．明确了解答求值问题的通法，再解答求值问题时，就可以有的放矢．