基于BP 神经网络算法的矩形顶管施工地表沉降预测研究

杨益平，王 威，陈丽波

（1.宁波市市政公用工程安全质量监督站，浙江 宁波315000；2.上海城建市政工程（集团）有限公司，上海市200333）

0 引 言

矩形顶管是一种在圆形顶管基础上改进的地下工程非开挖施工技术，具有大断面、空间利用率高的优点，自问世以来，已在地下工程领域有了广泛应用。矩形顶管工程多位于城市人口密集地区，周边环境复杂，对施工引起的地表沉降十分敏感，是施工控制的重点。

国内外对包括矩形顶管工程在内的非开挖地下工程引起的地表沉降的研究，根据方法不同大致可分为三个方向：一是目前应用最广泛、最简便的PECK 法，1969 年由学者PECK 根据实测资料提出经验公式，用来预估沉降槽曲线。二是以弹性力学为基础，根据事先假定的力学模型，利用软件进行地表变形的分析预测。包括有限元分析法、随机介质理论等。三是基于机器学习方法，建立数学模型，根据已知数据不断修改完善模型，进行预测，采用的模型包括神经网络、马尔科夫模型、Logistic 时间函数、遗传算法、灰色模型等。

PECK 公式在计算浅覆土非开挖地下工程地表沉降时与实测结果存在较大偏差，而应用弹性力学方法计算地表沉降时需假定很多边界条件，比如土体物理力学指标、施工工艺等，很多边界条件的取值依赖经验，一旦施工中发生变化或出现新的影响因素，将对计算结果产生很大影响。

BP 神经网络算法具有自学习和自适应的特点，经研究应用该方法预测地铁盾构施工引起的沉降，预测值和实测值拟合度较高，有很强的非线性映射能力，可以得到复杂的沉降规律。

本文基于BP 神经网络原理构建数学模型，以宁波市某矩形顶管地道工程地表沉降数据为例，计算地表沉降的预测值，通过与实测值的对比，验证该方法预测沉降的可行性，得出沉降规律，为矩形顶管施工地表沉降控制提供依据。

1 BP 神经网络模型基本原理

BP 神经网络（BackPropagation）1986 年由Rumelhart和McCelland 为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP 神经网络由输入层、隐含层和输出层组成，每层之间通过权值连接，BP 神经网络预测模型结构见图1。

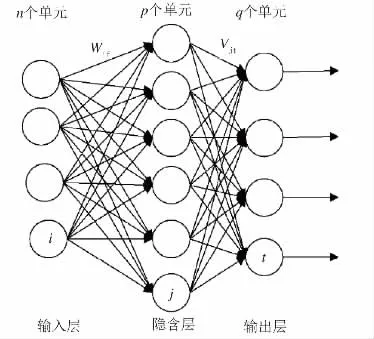
图1 BP 神经网络预测模型结构图

首先初始确定输入层与隐含层的权值Wmi隐含层和输入层的权值Wij。然后对输入层输入样本信息X；在输入层向隐含层传输样本信息过程中，对样本信息进行加权Wmi，即向隐含层输入加权信号；当隐含层神经元K向输出层传输信号时，对传输过程中的信号再次加权Wij，最后由输出层输出结果信息Y。当输出层输出信息误差无法满足需求时，网络会调整隐含层与输出层之间的权值Wij，隐含层与输入层之间的权值Wmi，计算误差对权值的梯度，并沿着反方向传播进行调整，反复训练调整

网络权值，直到误差越来越小满足需求为止[1]。

2 工程应用[2-6]

2.1 工程概况

宁波市某人行地道工程暗埋段采用矩形顶管工艺，钢筋混凝土顶管横截面规格为6.9 m×4.2 m，顶管单节长度1.5 m，总长度69 m。顶管覆土厚度为4.7～5 m。穿越土层主要为2-2a 淤泥质黏土层。主要施工设备为一台土压平衡顶管机。地道顶管上方为城市主干道，社会车流量较大。

为取得顶管施工期间地表沉降变形数据，在始发洞口水平距离21 m 位置设置了一个监测断面，以7.5m 间隔布置共5 个监测点，与顶管轴线垂直（见图2 中D17～D21）。

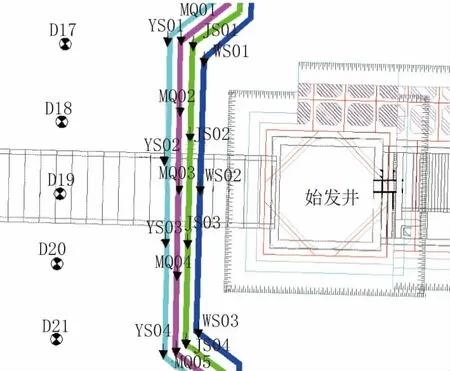
图2 监测布点平面图

沉降观测数据的采集周期为每日一次，从2018 年6 月22 日顶管机安装就绪，洞门完成破除开始，至2018 年7 月25 日顶管机进洞、地道贯通为止共34 期数据。

2.2 BP 神经网络的建立

2.2.1 网络结构和样本预处理

将该监测断面同一天的5 个监测点的数据编为一组，作为输入层的基础样本。考虑到BP 神经网络在样本数据较少的情况下收敛速度慢的特点，需要对样本进行预处理。采用时间序列法，以每2d数据为基础，将每组输入样本扩充为10 个。为了预测结果与实际观测值对比，输出样本的数量为5 个。根据朱伟刚等人的研究，隐藏层可以为单层也可以为多层，单层隐藏层可以在满足要求的同时避免收敛速度慢的问题。因此本文建立了一个3 层BP 神经网络模型，隐藏层为单层，见图3。

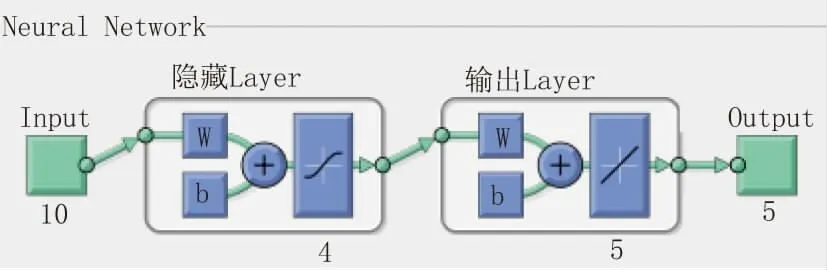
图33 层BP 神经网络模型结构图

2.2.2 样本划分

对34 组样本数据按照8∶2 的比例，选取前27 组数据为训练数据，后7 组数据为测试数据，见表1。由于样本数据范围较大，为了加快神经网络收敛速度，采用MATLAB 软件中的premnmx 函数对数据进行归一化处理，将其值域限定在（-1，1）之间。

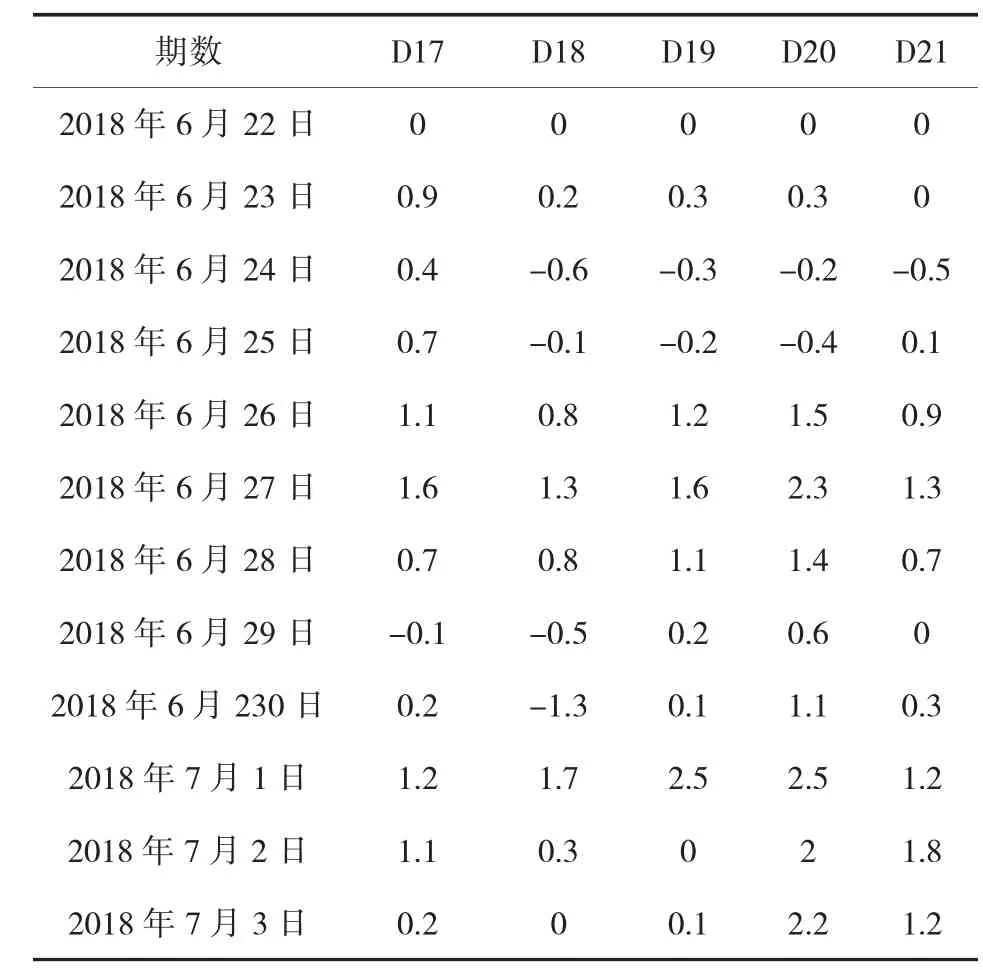
表1 部分样本数据

2.2.3 构建网络

利用MATLAB 神经网络工具箱中的newff 函数（前馈反向传播）构建网络，通过多次训练、反复修改参数，直到误差稳定收敛。本文设定的参数为：迭代次数2000 次；学习率0.01；目标精度0.01；隐藏层节点个数根据经验公式M=（n+m）0.5+a 计算，m 和n 分别为输入层和输出层的节点个数，a 为常数取1，隐藏层节点为4。得到的输出数据采用tramnmx 函数进行预处理，最后采用postmnmx 函数进行反归一化得到预测值。

2.3 地面沉降预测成果及分析

利用以上数学模型，经49 次学习训练后误差收敛，趋于稳定，训练结束，见图4。

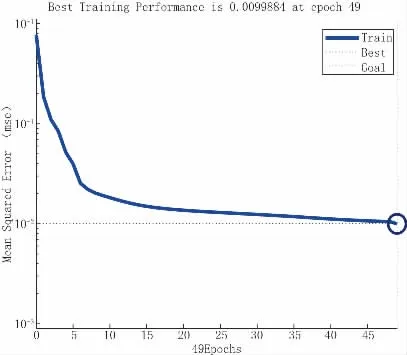
图4 训练误差收敛图

由表2 数据可以看出，同一个监测周期内，残差值的特征是在顶管轴线上的D19 号观测点最大，并向两侧逐渐收敛。D19 号观测点的残差值随着时间逐渐增大，见图5～图7。

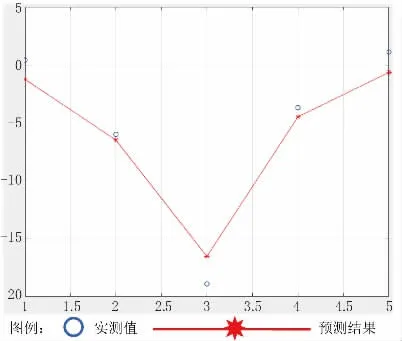
图57 月20 日实测值与预测结果对比

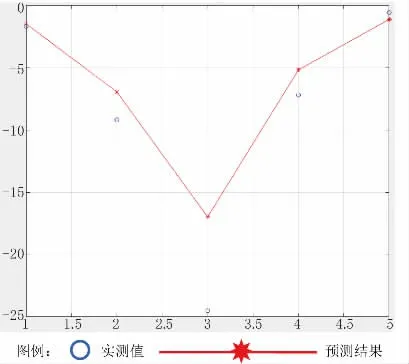
图67 月25 日实测值与预测结果对比

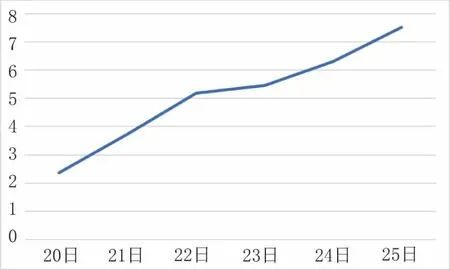
图7 D19 号点残差变化曲线

表2 实测值、预测值及残差数据对比表 mm

经过对现场施工记录分析，顶管机6 月22 日出洞，第1 天处于试顶进阶段，千斤顶压力、顶进速度、刀盘的电流强度、出土量、触变泥浆参数等都在不断摸索调整，至6 月23 日，顶管机开始进入稳定推进阶段，各项参数只有小幅变化。顶管机施工对土体产生扰动，是地表沉降的直接因素，在试顶进阶段，顶管机施工参数的不稳定造成了地表沉降变化的不规律。这一阶段的样本数据带有很强的“噪音”，如果加入训练可能最终导致预测值与实际值偏差过大。

为验证以上设想，将原来的34 组样本数据去掉第1 组，再以前26 组数据作为训练样本，后7组数据作为测试数据，经12 次训练后收敛稳定，成果见表3。

滤除带有“噪音”的样本数据后，可以看到每组预测数据仍然符合地表沉降槽“中间大，两边小”的特征，并且残差值明显减小，顶管轴线两侧的D17、D18、D20、D21 监测点的预测值基本围绕实测值上下波动，偏差在2 mm 以内。再次观察D19 号监测点，训练样本数据“降噪”前后的残差值对比见图8。可见最后一期残差值相比滤噪前下降了约47%，但随着预测时点远离训练样本数据，残差仍呈逐渐增加趋势。

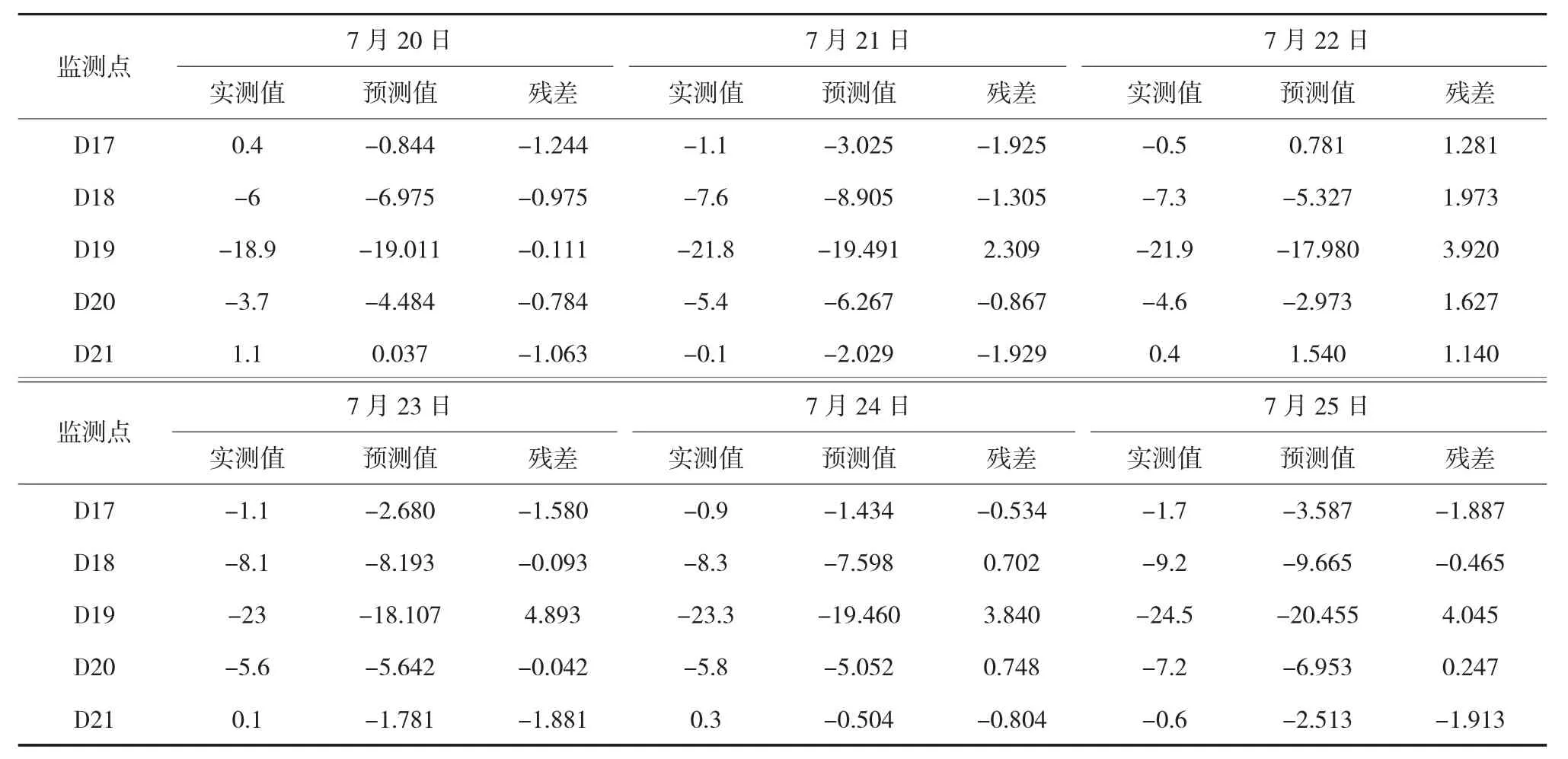
表3 滤除噪声后的实测值、预测值及残差数据对比表

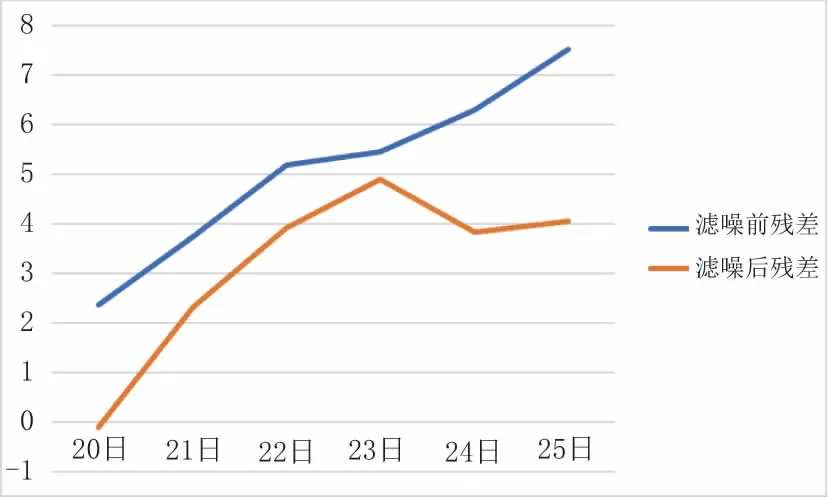
图8 D19 号点滤噪前后残差对比图

3 结 论

通过对以上数据的分析，可以看到采用BP 神经网络算法对淤泥质浅覆土矩形顶管施工过程中的地表沉降数据进行分析，能够利用其自学习、自适应的特点寻找地表沉降复杂规律，预测结果误差在顶管施工可以接受的范围内。数据分析也显示，训练样本对预测结果有很大影响，剔除不良样本、增加样本数量可以减少训练次数、加快收敛速度、提高预测精度，而近期预测结果的精度要好于远期预测结果。