基于ADAMS的750 KW风电齿轮箱的动力学仿真

唐贵基，刘梦凡,，王栋

(1.华北电力大学机械工程系，保定 071003；2.中能电力科技开发有限公司，北京 100034)

0 前言

齿轮箱作为风电机组中重要的传动部件，发生故障的几率较高，因此故障导致的经济损失也很大，所以对齿轮箱进行动力学分析，研究其动力学特性，对进一步提高齿轮箱系统的稳定性显得尤为重要。国内外学者对此问题已开展了相关的研究。2010 年，丁习坤[1]等建立了某750 KW 风力发电机传动系统，在ADAMS中进行了各轴转速、转矩及平行级齿轮啮合力的仿真计算，并对其最薄弱环节进行柔性体动力学分析；2013 年，赵三民[2]等建立了某型号的风电齿轮箱传动系统的虚拟样机模型并对其全刚体系统进行了动力学仿真，分析了平行级齿轮在运动过程中啮合力的变化规律；2015 年，Z Koishybayeva[3]等设计了一个差动行星齿轮箱，在 ADAMS 中建立其动力学模型，对仿真结果进行了分析，得出该行星齿轮箱在速度和转矩方面均具有稳定的输出值的结论。本文借助Pro/E 和ADAMS 建立了某型号风电齿轮箱传动系统的虚拟样机模型，不仅对平行级齿轮的啮合力进行了分析，而且对行星级的齿轮啮合力也进行了分析，并将仿真结果与理论值对比，结果较为接近，更加证明了模型的有效性。

1 虚拟样机模型

1.1 虚拟样机模型的建立

本文的研究对象为某750 KW 风电齿轮箱的齿轮传动部分，其结构为一级行星+ 两级平行。结构简图如图1 所示，各齿轮的基本参数如表1 所示。

本齿轮箱的传动系统的传动路线为：输入轴→行星架→行星轮→太阳轮→2 轴→斜齿轮1 →斜齿轮2 →3 轴→斜齿轮3 →斜齿轮4 →输出轴。

本文利用Pro/E 按照参数进行建模，然后将所有零件进行装配，最后进行干涉检查，得到无干涉的装配体。风电齿轮箱传动系统的装配图如图2 所示。

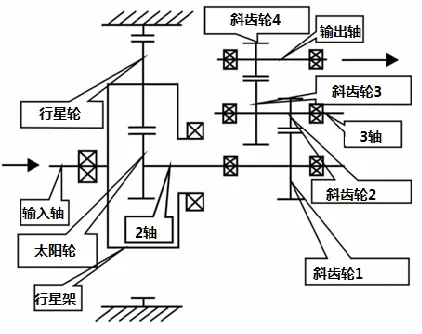
图1 某750 KW风电齿轮箱传动结构简图

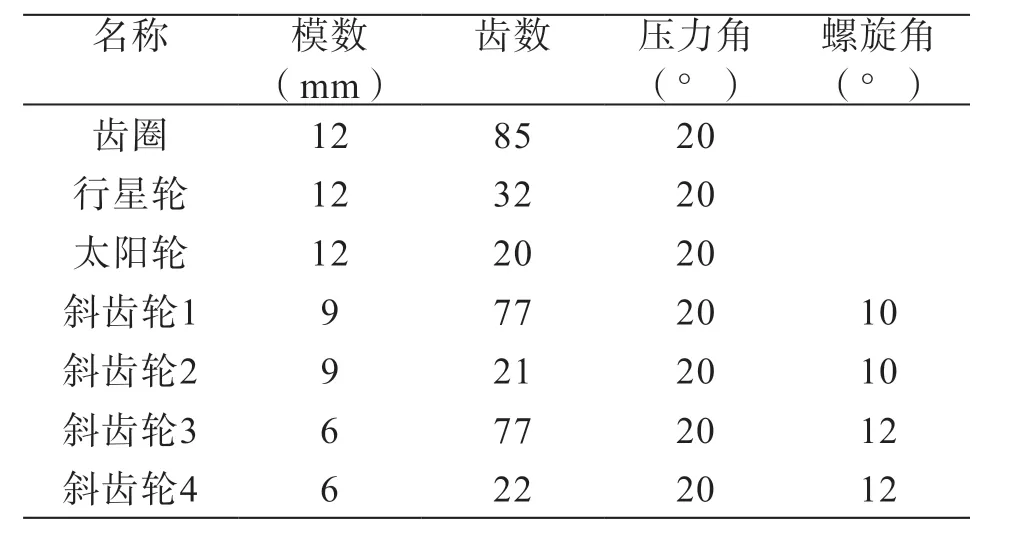
表1 风电齿轮箱传动系统的主要参数

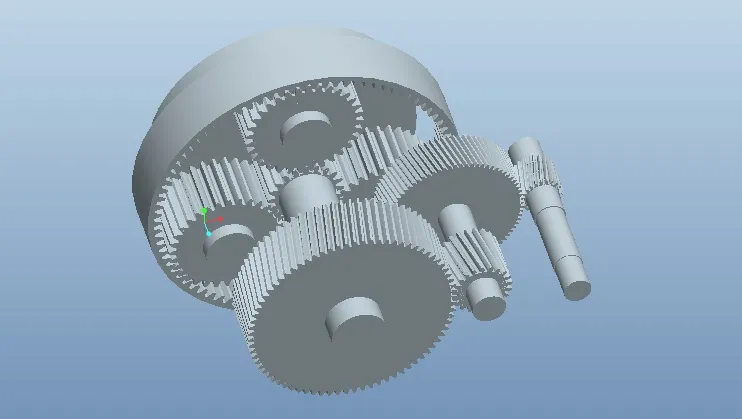
图2 风电齿轮箱传动系统装配图

1.2 数据的转换

专业的三维制图软件Pro/E 与动力学仿真软件ADAMS 之间的数据转换方法有两种[4]，一种是利用能够实现两者数据无缝连接的专用接口软件Mechanism/Pro 进行转换，另一种则是利用ADAMS 提供的数据接口导入三维数据。由于第一种方法必须使用含有此转换接口的软件版本,还需考虑电脑系统的兼容性，使用较为麻烦，所以本文将文件格式转换成质量和效率均优于其他格式的Parasolid 格式[5]。

1.3 斜齿轮啮合力的计算

本文通过动力学仿真得到各级的啮合力，为了验证仿真的正确性，需计算出各级啮合力大小的理论值，斜齿轮啮合力的计算公式为：

式中，T为齿轮传递的名义转矩；d为齿轮分度圆直径；β为螺旋角；αn为法面压力角；Ft、Fr、Fa分别为圆周力、径向力、轴向力。

1.4 直齿行星齿轮理论静态接触力计算

直齿行星齿轮理论静态接触力计算为[6]：

式中，T为太阳轮输出的转矩；K为行星轮系间载荷分配不平均系数；N为行星轮的个数；d为太阳轮的节圆直径；α为太阳轮的压力角；K与许多系数有关，经查阅文献[7]，最终通过计算得K=1.25。

1.5 啮合频率的计算公式

式中，fz为啮合频率；Z为齿数；n为转速。经计算得斜齿轮1、2 的啮合频率为134.75 Hz，斜齿轮3、4 的啮合频率为494.08 Hz。

2 动力学仿真及分析

2.1 约束、驱动以及载荷的施加

为了进行正确的动力学仿真，本文在齿轮传动系统上施加了相应的约束、驱动和载荷：行星架、2 轴、3 轴和输出轴相对于地面的旋转副；行星轮1，2，3 相对于行星架的旋转副；各转轴与齿轮之间是过盈配合，所以用固定副定义它们之间的约束关系；齿圈相对于地面的固定副；齿轮与齿轮之间施加实体-实体的接触。在行星架上施加一个由STEP 函数定义的旋转驱动，函数为step(time,0,0,0.03,120 d)，驱动类型选择速度（Velocity），并在输出轴上施加负载step(time,0,0,0.03,531 500 0)，单位为N∙mm。

2.2 仿真参数的设定

在齿轮运动过程中，接触区域附近会发生较为明显的变形，此时如果忽略齿轮之间的摩擦和齿轮的弹性波动，由Hertz 理论可以得到齿面的法向接触力与齿轮变形的关系为[8-11]：

式中，ρ为综合曲率半径；ρ1、ρ2为相互接触的两个齿轮的当量曲率半径（在“±”中“+”代表外啮合，“-”代表内啮合）；E1、E2为齿轮材料的弹性模量；ν1、ν2为齿轮材料的泊松比；E*为综合弹性模量。

对于两个啮合的齿轮，它们之间的接触刚度k的大小不仅与材料有关，而且与形状也有密切的联系，可以由关系式表达：

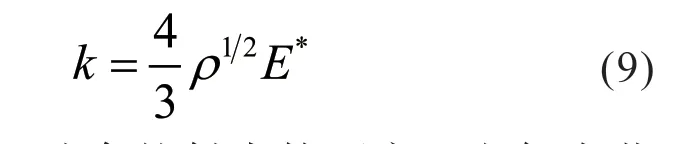
就两个相互啮合的斜齿轮而言，它们在节点处的端面曲率半径和法面曲率半径可以通过计算得到，表达式为：

其中

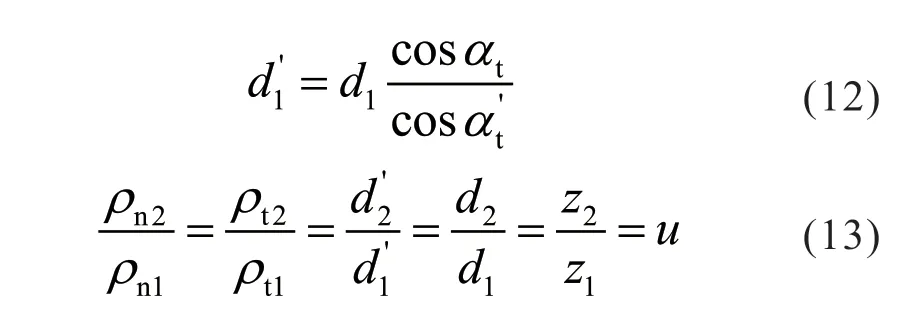
综合曲率半径为r：

将（10）、（11）、（12）、（13）式带入（14）式可以得到综合曲率半径的另一表达式：

式中，βb为基圆螺旋角；αt为端面压力角；αt为端面啮合角；d1、d2为两齿轮的分度圆直径，d1、d2为两齿轮的节圆直径。

最终得到接触刚度表达式为[12]：

将传动系统的三维实体模型导入到ADAMS 中后需要对各零件的材料进行设定，密度为7.801E-006 kg/mm3， 材料的弹性模量为2.071E+011 N/mm2，泊松比为0.29。经计算得到行星轮与太阳轮之间的刚度系数为1.294E+006N/mm2，行星轮与内齿圈的刚度系数为1.779E+006 N/mm2；中间级相互啮合的齿轮之间的刚度系数为7.819E+005 N/mm2；高速级啮合的齿轮之间的刚度系数为6.600E+005 N/mm2。材料刚度项的贡献值的指数设定为1.5，接触材料的阻尼大小取刚度系数的0.1%～1%，全阻尼时最大的穿透值为0.1 mm[13-16]。

2.3 仿真结果及分析

本文以高速级斜齿轮3、4 为例，对平行级齿轮间的啮合力进行分析。高速级齿轮对的啮合力仿真结果如下图所示。

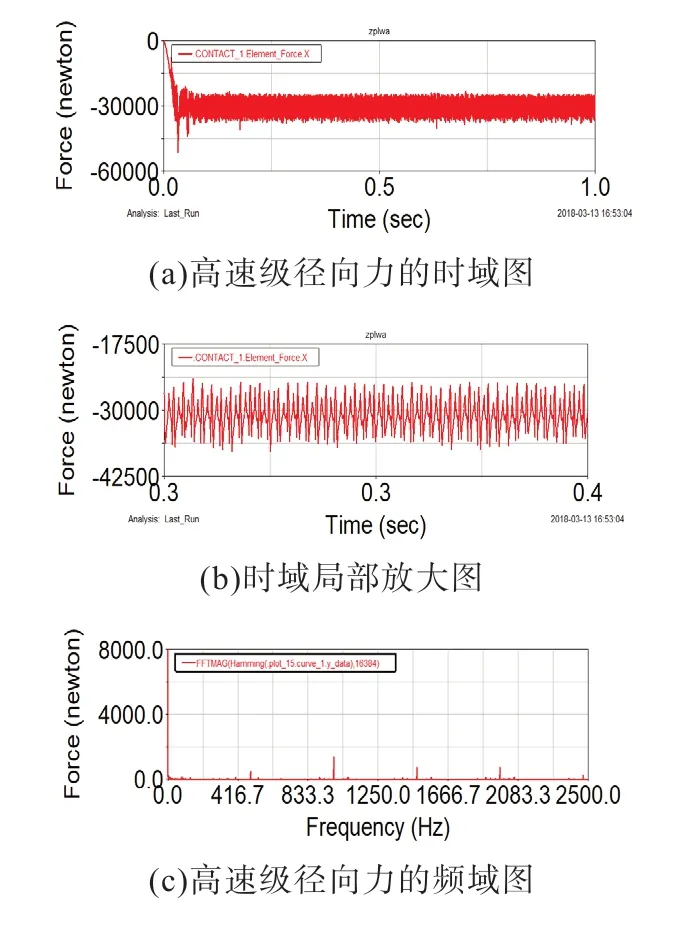
图3 高速级径向力的仿真结果

图5 高速级轴向力的仿真结果

从时域上分析，图3(a)～图5(a)中0～0.03 s这段时间，力较为平缓的增加，没有发生陡变现象，这是由于在保持架上施加了STEP 函数。从图3(b) 看出，0.03 s 之后力在某个值附近上下波动且具有周期性，趋势比较平稳，符合齿轮传动过程中周期性啮入啮出的特点。论文中取平稳阶段的平均值作为各方向上的仿真值。由表2 得高速级径向力的平均值为30830.1 N，与理论值的相对误差为5.1%，高速级切向力的平均值为77732.4 N，与理论值的相对误差为1.3%，高速级轴向力的平均值为16530.8 N，与理论值的相对误差为1.3%。

从频域上进行分析，在图3(c)，图4(b) 和图5(b) 中均在与494.03 Hz 相近的频率处出现了较为明显的谱线，此频率与高速级齿轮对的啮合频率基本吻合，在其二、三、四倍频处出现的谱线更为明显。高速级和行星级的齿轮啮合力的比较如表2 所示。

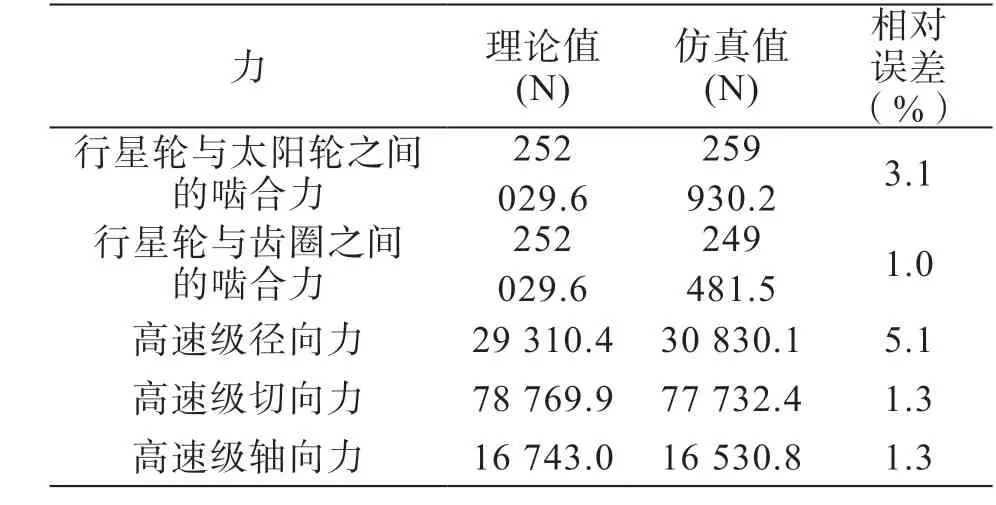
表2 啮合力的仿真值与理论值的比较

行星轮和太阳轮之间的啮合力的分析方法和行星轮和内齿圈的分析方法一样，为了避免冗余，本文以行星轮和太阳轮之间的啮合力计算为例，分析直齿行星轮系间啮合力的运动规律。根据行星轮的运动规律，由式（4）计算出行星轮所受到的啮合力大小为252029.6 N，其两个分力大小为[17]：

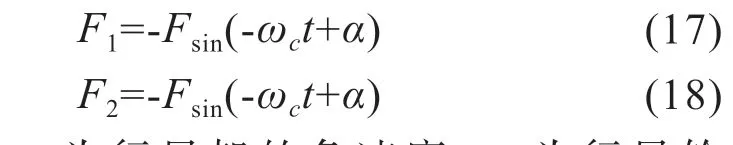
其中，wc为行星架的角速度，α为行星轮的压力角，F1为行星轮与太阳轮之间的径向力，F2为行星轮和太阳轮之间的切向力。

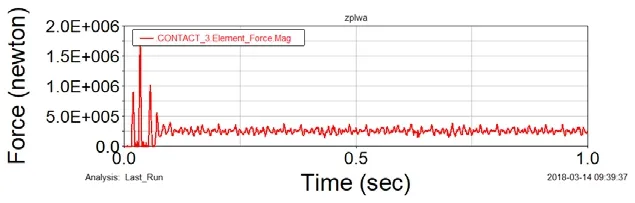
图6 行星轮和太阳轮之间啮合力的时域图

利用MATLAB 将行星轮所受的各分力的理论值曲线绘制出来，再将ADAMS 仿真的结果导出并保存为*.txt 格式，然后导入到MATLAB中进行绘制，两者比较结果如下图所示。

图7 行星轮与太阳轮之间的径向力

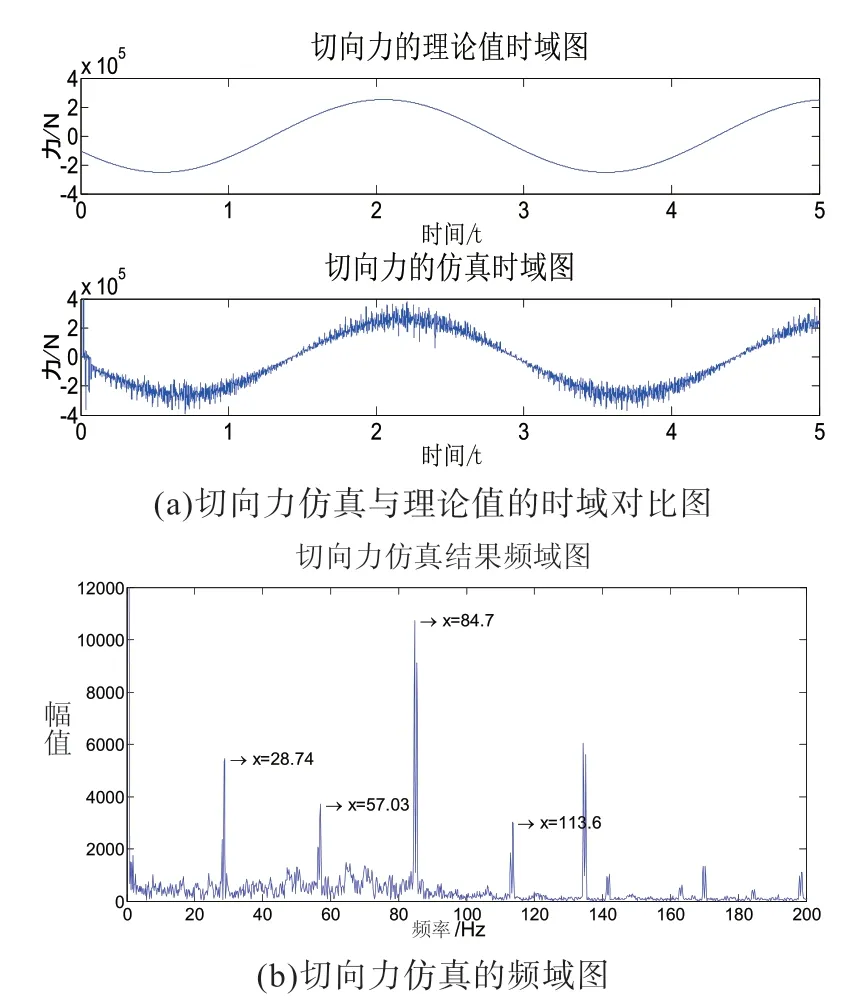
图8 行星轮和太阳轮之间的切向力

从时域上进行分析，由图7(a) 和图8(a) 对比可知，行星轮和太阳轮之间的径向力和切向力变化显著,呈现明显的周期性，并且两者的仿真结果与理论值的变化趋势基本一致，只是在相位上相差大约90 度，仿真结果的波动范围均为-4E+005 N～4E+005 N，这与理论值的波动范围也基本一致，但比理论值偏大。

从频域上进行分析，在图7(b)和图8(b)中出现了与行星轮的公转频率0.3 Hz 很接近的谱线且幅值较高，还出现了和行星轮与太阳轮的啮合频率28.33 Hz 及其倍频相接近的谱线。

综上所述，各级啮合力的仿真结果与理论值均存在一定的误差，但最终的结果满足误差要求。出现误差的原因主要有以下几个方面：第一，风电齿轮箱在实际运转中，齿轮之间的啮合刚度是时变的，而在论文中，刚度系数是以Hertz 理论为基础计算得到的，是恒定不变的。第二，接触力参数的设定存在一定的误差，例如阻尼系数、最大切入深度等，这些参数是靠经验得来的，而理论值的计算并不会考虑这些参数。第三，在仿真结果的计算方面，论文是选取平稳阶段的某时间段内的平均值，所以在数值上有可能存在一定的偏差。

3 结束语

论文利用Pro/E 建立风电齿轮箱的虚拟样机模型，然后用动力学分析软件ADAMS 对其进行动力学仿真，得到各级啮合力的时域图和频谱图，最后对仿真结果进行分析。仿真结果与其相对应的理论值较为接近，在误差允许范围内并且与实际的运动规律相符，同时为进一步研究故障工况下的齿轮箱的动特性提供了依据。