多目标决策Geoffrion法在光伏发电投资中的应用

莫荣超，马 进，张 芹

（华北电力大学 控制与计算机工程学院，河北 保定 071003）

0 引言

随着国际能源日益紧张，环境保护、节能减排已成为当今各国的发展方向。太阳能是世界上最丰富环保的能源，发展利用太阳能也是世界实现人与自然和谐发展的重要举措之一。中国作为世界上最大的光伏产业国，向各国出口大量光伏板，然而国内消费不到产能的15%，光伏行业经济过度依赖出口。近两年，国外市场光伏产业几乎达到饱和，经济放缓，市场疲软，特别是中美贸易战使得出口产品附上高额税率，影响了中国光伏行业的经济发展。改变依靠出口国外的消费局面，尽快发展国内市场并寻求政府支持是当前光伏产业转型的方向[1]。发改委发布的[2019]761号文件明确对光伏发电补贴，电价补贴为0.42 元/KW∙h[2]。这一政策使得投资者对光伏行业产生浓厚兴趣，国内市场前景也越来越广阔。

目前，国内许多学者对光电投资进行了研究和评价，其关注点主要集中在发电可靠性、政府补贴、并网效益、投资风险等定性评价，尚未对电网数据和政府工作报告中关于光伏发电的成本数据及收益数据进行定量分析，形成一个具体的数据模型，指出投资可行性[3-5]。文献[6]采用B/C 法评价了光伏电价补贴方式优于建设补贴方式，但并未给出投资方式；文献[7]分析了屋顶式光伏发电系统经济性受影响的因素, 并提出了一些提高其效益的建议，但缺乏数据指导。文献[8]运用了传统的层次分析法（AHP）、逼近理想排序法（TOPSIS）对光伏发电进行了可靠性、经济性综合评价。

在综合比较各方法后，针对投资风险中的多目标决策，提出Geoffrion 法计算分析，用直观的效益数据展现出投资可行性，并面向企业客户和个人用户，为投资者提供理论及数据依据。

1 多目标决策的Geoffrion法

Geoffrion 法[9]是A M Geoffrion 在1970 年提出用来求解多目标决策问题，多目标函数设为：v(f(x))=v(f1(x),…, fn(x))，最终转换为求方程式最佳解：max{v(f(x))=v(f1(x),…, fn(x))}，x ∈X，X={x ∈RN|Ax ≤b，x ≥0，∂v/∂fl>0，A 是m×N 的系数矩阵。x，b，0 均为N 维列向量，假设所有的fi(x)，i=1,2,…,n 是紧、凸集，v 是X 上的凹函数，且在他们的定义域上连续可微。以v(f(x))的一阶泰勒展开线性逼近v(f(x))[记做v(x)]：

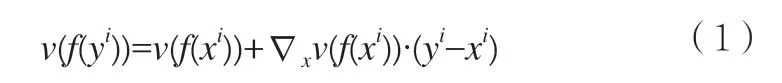
极大值等价于求：max[∇xv(x)]∙yi，yi∈X，因此

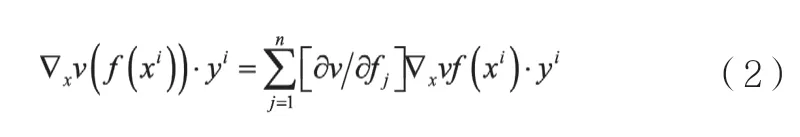
式（2）两边同除以∂v/∂fl，由于∂v/∂fl>0，这样不改变函数值的梯度方向，得到：，记mlj=，则式

（2）的目标函数等价于：

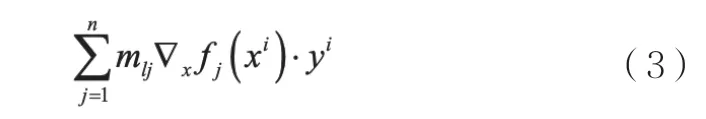
称mlj为边际置换率（MRS），在多目标决策中，通过由决策者提供的两组目标函数f 和f '来计算MRS 值，即f=(f1, f2, f3…fn)，f'=(f1, f2,…fi+Δfi,…, fj+Δfj,…, fn)。首先，确定一个极小的增量Δfi，由此计算边际置换率：mlj=Δfi/Δfj，j=1,2,…,n，j≠i。

得出mlj后，由于目标函数fj(x),j=1,2,…,n 是已知的，▽xfj(xi)可以计算。因此，可以用式（3）计算yi，得到搜索方向d=yi-xi。解决了搜索方向后，接下来确定步长，步长由决策人提供信息来确定，将[0,1]上选择合适的步长α，计算不同α 值的fj（xi+αdi），j=1,2,…,n，并将其以表格或图饼的形式递交决策人，让其选择一组最满意的目标函数值，此时α 为最佳步长。

当xi=xi+1时，迭代计算就可以终止。但由于决策者确定信息的精度不高，因而需要有一个实际的终止准则：

综上所述，Geoffrion 法步骤如图1 所示，其算法可总结为以下5 个步骤：第一步，确定初始值xi，xi∈X，且i=1；第二步，计算边际置换率mlj；第三步，由公式（3），求出yi，并得到d=yi-xi；第四步，让决策者在[0,1]内选择合适步长；第五步，若Δq/Δ1≤δ，停止迭代，否则让i=i+1从第二步重新开始。

2 Geoffrion法在光伏发电投资中的应用

文中的数据来自电力行业发展年度报告，以5 年为时间单位，通过对各地成本及收益重新使用Geoffrion 法进行建模计算分析，结果可作为投资者参考。

1）建立模型

收益最大，维护最小，投资最少作为目标。数学模型为{f1(x), f2(x), f3(x)}，其中x 是决策变量，f1(x)是负的利润函数，f2(x)是投资费用，f3(x)是维护费用。

2）决策过程及计算分析

第一次无差异折衷如下，给定初始值xi，相应的目标函数：f1(x)=（-6483，941，4113）。

在该点估计边际置换率，对f1(x)～f3(x)有：（-6483，941，4113）～（-6483-42，941，4113+18），对于f1(x)～f2(x)有：（-6483，941，4113）～（-6483-60，941+8，4113），边际置换率：=1，=Δf1/Δf2=-(-60)/8=7.5，Δf1/Δf3=-(-42)/18=2.33。

计算结果如表1 所示。

（下表的收益、维护费、投资单位均为：元）。

观察表1 并选取6 号组作为第二次迭代初始值x2。

第二次无差异折衷如下，给定初始值x2，相应的目标函数：

f2(x)=(-6998，998，4639)，边际置换率：=1，=Δf1/Δf2=-(-41)/3.2=12.81，=Δf1/Δf3=-(-41)/15.3=2.68。

计算结果如表2 所示。

观察表2 并选取6 号组作为第三次迭代初始值x3。

第三次无差异折衷如下：给定初始值x3，相应的目标函数：f3(x)=(-7101，1012，4649) 边 际 置 换 率mlj：=1，

计算结果如表3 所示。

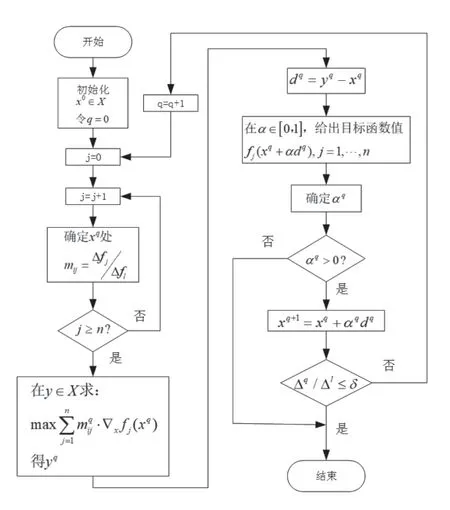
图1 Geoffrion法流程图Fig.1 Flow chart of Geoffrion method

观察表3 并选取6 号组作为第四次迭代初始值x4。

第四次无差异折衷如下：给定初始值x4，相应的目标函数：

表1 第一次迭代计算结果Table 1 The first iteration calculation result

表2 第二次迭代计算结果Table 2 The second iteration calculation result

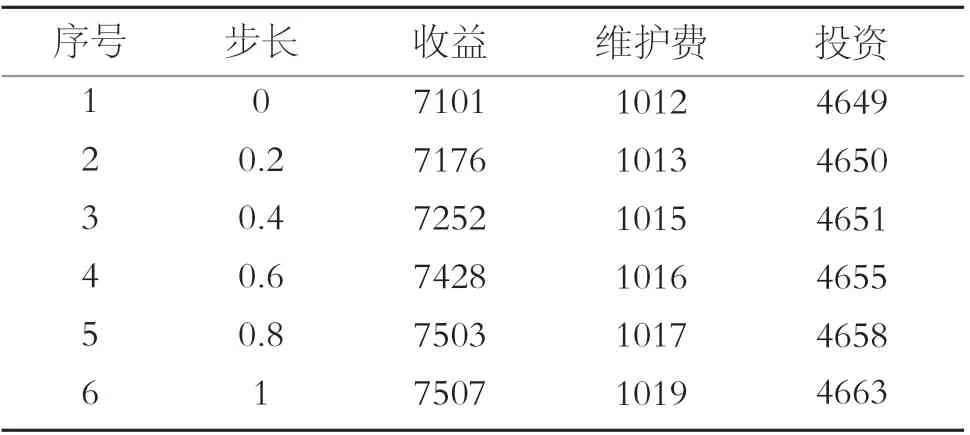
表3 第三次迭代计算结果Table 3 The third iteration calculation result

f3(x)=(-7507，1019，4663)计算边际置换率

计算结果如表4 所示。

由表4 可知，在投资和维护费增加幅度不大的情况下，利润下降。因此，序号1 数值组认为是最优目标函数值，则f3(x)=(-7507，1019，4663)是该模型最优解。

3 数据对比分析

在光伏发电现有技术下，铺设1000 瓦光伏电站（占地面积约10m2），按照Geoffrion 算法可得收益7507 元人民币，投资费用为4663 元，维护费用1019 元。一般方案铺设1060w（占地面积约11m2），收益7326 元，投资5043元，维护费用1239 元。

由此可知，装板面积增加的同时，收益相差不大，但维护费和投资费用均增加很多，所以本方案带来的经济效益是好的，可以推荐给投资者。

表4 第四次迭代计算结果Table 4 The fourth iteration calculation result

4 结论

Geoffrion 法通过把决策者的需求信息同分析者的算法结合起来，使误差精度降到最小，同时也给出了客观的数据视图。与以往的定性研究文献不同，本文通过定量分析投入和产出，让投资者可以直观地进行决策分析。该算法模型较大，处理数据较多，但其优化后的结果可作为判断投资的重要参考。