蟠龙抽水蓄能电站地下厂房区初始地应力场反演方法比较分析

徐卫中，胡光平，周曙光，胡绍沛

(1.重庆蟠龙抽水蓄能电站有限公司，重庆401452； 2.河海大学水利水电学院，江苏南京210098)

0 引 言

岩体初始地应力场是地下工程开挖与支护结构设计所需要的基本因素之一，直接影响工程设计与施工的可靠性与安全性。实测地应力是了解区域地应力场最直接的途径，但在工程现场，由于场地和经费等原因，不能进行大量测量。因此需根据实测的地应力资料，结合地形地貌、地质构造等条件，通过有效的分析方法进行反演计算，以获得更为准确的、适应范围较大的地应力场。目前国内外初始地应力场反演方法多为多元回归、神经网络和遗传算法，如付成华等[1]分别采用多种算法反演了溪洛渡水电站工程坝区的初始地应力场，张勇慧等[2]对大岗山水电站地下厂房地应力场进行了回归反演，张强勇[3]等对双江口水电站地下厂房区三维初始地应力进行多元回归反演；周洪福等[4]通过对三维模型施加不同的边界载荷，采用三维数值分析方法对江坪河水电站坝址区初始地应力场进行反演；张继勋等[5]对锦屏二级水电站引水隧洞的高地应力及岩爆问题进行了分析；董志高等[6]建立了多元回归模型，求解回归系数、从而获取厂区初始地应力场；蒋中明等[7]采用人工神经网络理论对考虑断层影响的地应力场进行了反演；裴启涛等[8]采用遗传神经网络法反演了加塔坝区的初始地应力场。本文根据重庆蟠龙抽水蓄能电站工程地下厂房区域的工程地质资料和实测地应力资料，分别采用多元回归、神经网络和遗传算法对地下厂房区域的初始地应力场进行反演并对结果进行比较分析。

1 工程概况

重庆蟠龙抽水蓄能电站位于重庆市綦江区中峰镇境内，地处东经106°27'，北纬28°51'。上水库位于綦江一级支流清溪河右岸支流蟠龙沟上游，下水库位于清溪河右岸支流石家沟上。该电站由上水库、输水系统、地下厂房系统、下水库及地面开关站等建筑物组成。电站装机容量1 200 MW(4×300 MW)，属一等大(1)型工程，主要永久性建筑物按1级建筑物设计，次要永久性建筑物按3级建筑物设计。地下洞室穿越夹关组(K2j)和蓬莱镇组(J3p)两套地层主要由砾岩、砂岩、粉砂岩、泥质粉砂岩、泥岩、粉砂质泥岩组成。

工程分别在主厂房、主变室和高压岔管附近完整岩体中采用水压致裂法进行了地应力测试，实测地应力成果见表1。

表1 实测主应力值

注：①大地坐标系定义为X轴为正北，Y轴正西，Z轴铅直向上。②σ为主应力值，正号为拉应力、负号为压应力；α为主应力与x坐标间的夹角；β为主应力与y坐标间的夹角。

2 计算原理

2.1 多元回归方法

(1)

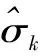
(2)

根据最小二乘法原理，使得S残为最小值的方程式为

(3)

表2 各类岩体的材料参数

解方程式(3)可以得，n个待定回归系数L=(L1，L2，…，Ln)T，则计算域内任一点P的回归初始应力，由该点各工况有限元计算值迭加可得

(4)

2.2 神经网络方法

神经网络模拟人脑的结构和机理以实现人脑的某些功能，可自动建立输入和输出的高维非线性映射，在解决复杂的非线性问题时，不需要假定一个具体的函数形式，从而大大简化了求解的难度。其具有高度的非线性函数映射功能，具有自组织、自学习、非线性动态处理等特征，能够对数据进行很好的拟合[9]。

采用神经网络法进行地应力场计算，首先建立初始地应力场和边界载荷之间的非线性映射关系，以测点应力为输入，输出即为对应的边界条件组合；然后代入数值模型中计算，得到岩体初始应力场。神经网络模型拓扑结构包括输入层、隐层和输出层。

2.3 遗传算法

遗传算法是一种全局最优化方法，特别适用于多极值点的优化问题，将选择、交叉、变异等概念引入到算法中，通过构成一组初始可行解群体并对其进行操作，使其逐渐移向最优解。假设以岩土介质应力系数作为反演变量，利用遗传算法的3个基本操作(即选择、交叉和变异)模拟自然选择和自然遗传过程中的繁殖、交配和变异现象，从待反演参数组成的解种群中逐代产生新的群体，比较个体，最终搜索到最优个体，即为反演的应力系数。

3 数值计算模型

通过分析重庆蟠龙抽水蓄能电站工程区范围、地应力测点的分布情况和工程地质条件，建立地应力反演模型。坐标原点取在1号机组中心，原点高程451.9 m。主厂房轴线方向为X轴，以指向副厂房方向为正；垂直于主厂房轴线方向为Y轴，以指向主变室方向为正；竖直方向为Z轴，以向上为正。反演模型计算范围：X轴方向取1 726 m，Y轴方向取1 695 m，Z轴方向从0 m高程处取至地表，三维有限元模型如图1所示，共剖分了574 757个单元，101 132个节点。数值计算中所选用的各类岩体的材料参数如表2所示。

图1 三维有限元模型

4 计算结果与分析

4.1 多元回归方法计算结果

根据实测地应力资料和6个工况下实测点的计算应力值，采用最小二乘法进行多元回归计算，得到6个边界条件——自重、X向挤压、Y向挤压、XY面剪切、YZ面剪切、XZ面剪切的回归系数L1=1.16，L2=6.01，L3=-0.017，L4=-2.22，L5=2.30，L6=8.18。

4.2 神经网络方法计算结果

根据多元回归方法的成果，通过试算确定待反演参数的取值范围，如表3所示。

表3 待反演参数的取值范围

使用MATLAB对6个参数随机取值组合，得到99种参数组合方案，分别用这些参数组合方案对6种边界条件下输出的实测点应力分量值进行线性组合，得到99组实测点应力分量计算值。以实测点应力分量计算值作为网络输入，参数组合作为网络输出，可组织99个样本，经试算，建立网络模型，取学习率为0.1，误差ε=0.04，利用组织好的样本集对网络进行训练，网络经过100 000次学习达到精度要求。然后将测点的实测应力值输入训练好的网络进行反演计算，网络输出即为反演所得参数：L1=1.14,L2=6.62,L3=-0.000 4,L4=-3.16,L5=3.13，L6=7.95。

表4 三种方法应力分量反演结果对比 MPa

注：应力以拉为正，压为负。

4.3 遗传算法计算结果

根据多元回归方法的成果，通过试算确定待反演参数的取值范围，如表3所示。

遗传算法各运行参数为：每代群体规模100；由于个体由L1、L2、L3、L4、L5和L6组成，故每个个体所含变量个数为6；指定将生存到下一代的个体数取10；交叉概率取为0.75；进化代数取100；停滞代数取10。用MATLAB进行反演计算，求得最佳个体所对应的L1=1.21，L2=6.54，L3=-0.07，L4=-2.79，L5=2.92，L6=8.77。

4.4 反演计算结果比较分析

将三种方法反演所得参数转化为边界条件，分别作用于有限元模型进行弹性有限元计算，得到的应力场即为初始地应力场。

将地应力测点的应力分量实测值和三种方法的计算值进行对比，如表4所示。

从表4可以得出：

(1)多元回归方法、神经网络方法和遗传算法反演得到的初始地应力结果基本一致，均能反映实际地应力场分布规律。

(2)反演计算值与实测地应力在大小上比较吻合。多元回归反演计算值与实测值的最小误差为0.04%，最大误差为17.01%，其余测点误差在5%左右；神经网络最小误差为0.22%，最大误差为16.45%，其余测点误差在6%左右；遗传算法最小误差为0.19%，最大误差为18.80%，其余测点误差在7%左右。通过反演计算所得的初始地应力场是合理可靠的。

(3)三种方法中，多元回归方法反演计算出的地应力场结果与实测应力值的误差最小。对比各方法的计算过程，神经网络和遗传算法计算结果的波动范围相对较大，且遗传算法计算时间相对较长。

5 结 论

本文根据重庆蟠龙抽水蓄能电站地下厂房区实测地应力资料，分别采用多元回归、神经网络和遗传算法对地下厂房区初始地应力场进行反演计算。反演结果表明，地应力反演计算值与实测值比较吻合，各方法计算结果也基本一致，其中多元回归方法所得结果的误差相对较小、耗时较短。分析成果可为后续的施工方法和支护方案研究提供参考。