一种改进的Bingham岩石蠕变模型研究

王 唯，刘远明

(贵州大学土木工程学院，贵州贵阳550025)

0 引 言

在诸多岩土工程实际中，广泛涉及岩石蠕变问题。因此，岩石蠕变方面的研究具有非常重要的理论意义。近年来，随着技术手段和理论的创新，岩石流变领域的发展取得了丰硕的成果。许多研究学者通过将简单的弹性、粘性及塑性元件串并联组合成复杂的模型来描述流变现象。由于受到加载水平的限制，能描述岩石蠕变全过程的模型并不多，尤其是加速蠕变阶段。学者们对模型参数进行了改进，取得良好的研究成果[1-2]。夏才初等[3]基于基本流变力学模型进行串联组合，形成15个流变力学模型，并提出辨识模型的方法；朱昌星等[4]将能够描述加速流变特性的时效损伤变量引入岩石非线性蠕变损伤模型中，并结合板岩剪切流变试验验证了模型的合理性；杨圣奇等[5]对龙滩水电站泥板岩进行剪切流变试验，将非线性流变元件与西原模型串联起来，建立了新的能够描述加速流变特性的岩石非线性流变模型；赵延林等[6]对橄榄岩试样进行流变试验，提出由瞬弹性Hooke体、塑性体、改进Bingham体串联形成的非线性粘塑性流变模型，能反应不同应力水平下岩石流变规律；孙钧院士[7]对非线性流变问题的求解提供了2种方案：一种是由试验拟合的经验本构关系式，另一种是在粘塑性部分内加上一项非线性的经验粘性元件作为对线性流变模型的修正；唐佳[8]等对白云石英片岩和绿泥钠长片岩进行蠕变试验，基于应力-应变曲线，提出在Mohr-Coulomb准则基础上引入新的M-C塑性元件，构成了改进的Burgers蠕变模型。

综上，岩石蠕变本构模型建立过程中，通过将模型中的线性元件替换为非线性元件，即可得到能够描述岩石的加速蠕变过程。本文在已有的流变理论基础上，建立了一种新的对非线性岩石流变本构模型。

1 非线性流变模型的建立

1.1 岩石的蠕变曲线

岩石的蠕变曲线图1[9]。图中，3条蠕变曲线是在不同的应力条件下得到的。其中，σa>σb>σc。当岩石在低应力水平的恒定荷载持续作用下时，应变量虽然会随时间有所增加，但是蠕变变形的速率会逐渐减小，最后会趋于一个稳定的数值。当应力水平较大时，曲线不在稳定于一个定值，而是无限增加直到破坏。根据应变速率的不同，将蠕变过程划分为3个阶段：第一蠕变阶段(曲线中ab段)，应变速率随时间的增加而减小，称为减速蠕变阶段；第二蠕变阶段(曲线中bc段)应变速率保持不变，称为等速蠕变阶段；第三蠕变阶段(曲线中cd段)，应变速率迅速增加直到岩石破坏，称为加速蠕变破坏。

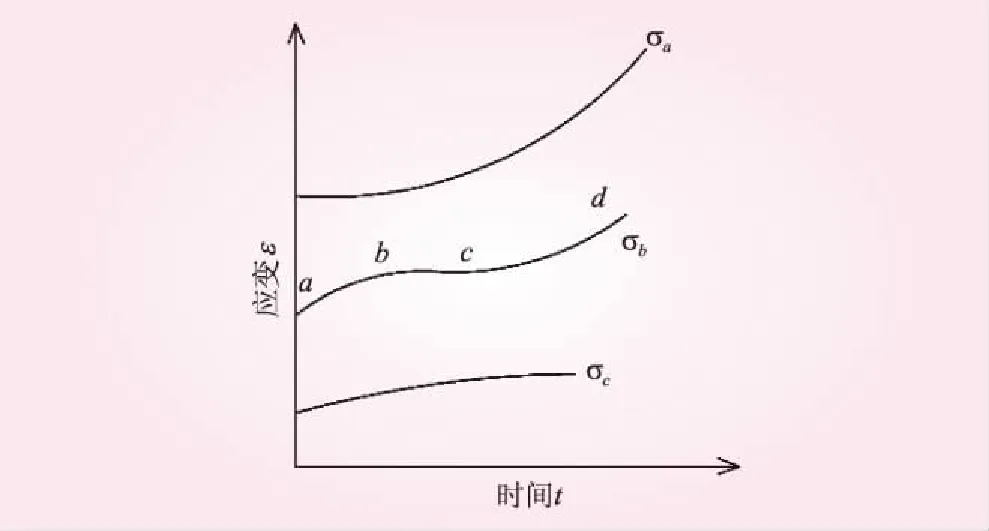
图1 岩石蠕变曲线

由于传统的元件基本都是线性的，无论通过何种串并联组合方式，只能描述其减速和等速蠕变。因此，通过引入非线性粘滞系数的牛顿体，与应力阀值并联组合新元件来描述加速蠕变的过程。

1.2 非线性Bingham模型的改进

传统的Bingham模型由1个塑性元件与牛顿粘壶并联后再与1个Hooke体串联。蠕变方程为

(1)

式中，ε为蠕变量；E和η为蠕变系数；t为蠕变时间；σs为应力阀值。传统的Bingham模型见图2。

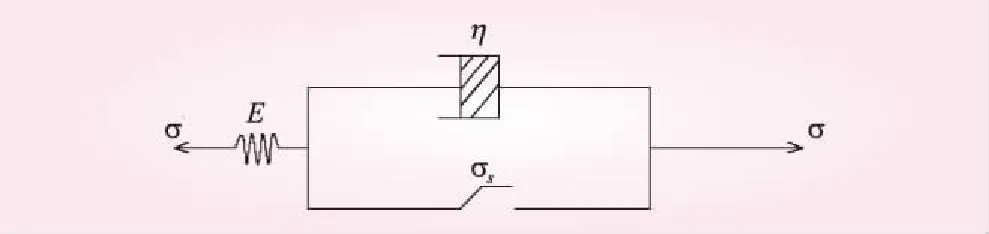
图2 传统的Bingham模型

当作用应力水平时，传统的Bingham的蠕变量随时间呈线性关系。然而在工程实际中，岩石蠕变通常表现为非线性的函数关系；而传统的Bingham模型只能描述稳态蠕变，并不能描述整个岩石的蠕变过程。因此，通过将Binham模型中的某些线性元件替换为非线元件，可建立描述岩石蠕变全过程的改进的Bingham模型。

为描述岩石的加速蠕变与衰减蠕变过程，曹树刚等[10]提出粘滞系数是时间的函数关系；宋飞等[11]提出粘滞系数是应力水平与时间的函数关系；周家文等[12]基于流变伺服仪得到绿片岩三轴试验数据，构造出能够模拟岩石衰减蠕变和加速蠕变特征的非线性函数；马林建等[13]对盐岩的三轴压缩试验表明，盐岩的弹性模量随加载的时间呈指数递减趋势。本文基于流变力学理论，假定在静力荷载作用下，该模型的弹性元件系数与时间t呈衰减趋势，衰减规律为

E2(α)=E2/[1-exp(-αt)]

(2)

式中，E2为Bingham模型弹性元件初值，该参数主要反映岩石的瞬时弹性特性；α为控制弹性系数衰减的无量纲参数，可由试验测定。

则Hooke体的一维方程为

(3)

当σ=σ0时，蠕变方程为

(4)

对于描述岩石加速蠕变阶段，不少文献中组合模型的粘滞体不再是常值，而是用非线性牛顿体来代替。因此，本文从粘滞系数入手，用幂函数形式的粘塑性体来描述岩石加速蠕变随时间的变化关系。非线性牛顿体的一维方程为

(5)

(6)

本文基于传统的Binham模型，将模型中的常值牛顿粘体替换为非线性的牛顿体，并串联1个描述岩石弹性衰减的Hooke体，建立了如图3所示的改进的Binham模型。图中，通过引入开关应力阀值σs来表示岩石材料加速蠕变的初始应力，只有当σ>σs时，并联的粘塑性体才会发生作用。其中，原模型弹性体描述岩石的瞬时弹性变形，非线性弹性体描述岩石的衰减蠕变，粘塑性体描述岩石的加速蠕变。

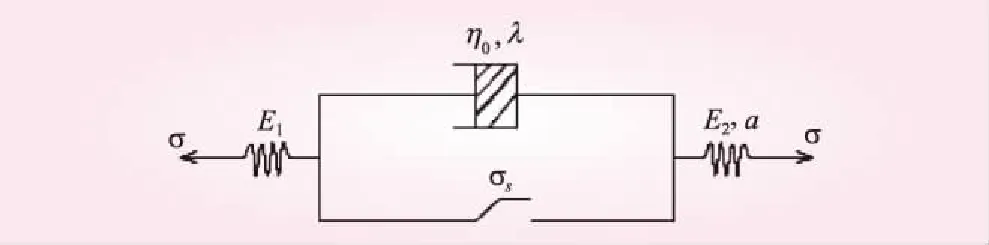
图3 改进的Bingham流变模型

根据流变力学相关理论，串联组合各元件上应力相等，总应变等于各元件应变和。可得基于图3的状态方程如下

σ=σ1=σ2=σ3

(7)

ε=ε1+ε2+ε3

(8)

σ1=E1ε1

(9)

(10)

(11)

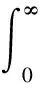
(1) 当σ≤σs时，该模型退化为2个弹性体串联，本构方程为

(12)

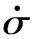
(2)当σ>σs时，有

(13)

1.3 一维蠕变方程

令σ=σ0H(t)，代入式(12)、(13)本构方程中，方程两边经过Laplace变换以及逆变换可得到蠕变方程。

(1)当σ≤σs时，有

(14)

(2)当σ>σs时，有

(15)

1.4 三维蠕变方程

在三维应力状态下，流变方程很难用形象具体的元件去描述。参照弹性力学方法，将岩石内部1点的应力张量σij分解为球应力张量σm和偏应力张量Sij这2个部分，岩石的三轴应力状态可由3个不变的主应力σ1、σ2、σ3表示，即

(16)

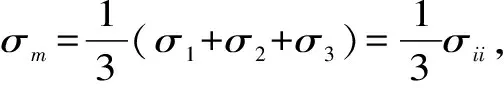
(17)

同理，也可将应变张量εij分解为球应变张量εm和偏应变张量eij，即

εij=eij+δijεm

(18)

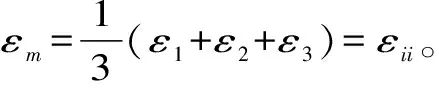
对于大多数各向同性材料而言，一般条件下均存在以下规律[14]：球应变张量只与球应力张量有关，而偏应变张量只与偏应力张量有关，这给建立三维本构方程带来很大方便。对于一般的线弹性材料而言，球应变张量与偏应变张量分别与球应力张量与偏应力张量成正比。对于弹塑性材料，在塑性范围内，球应变张量与球应力张量成正比，偏应力张量与偏应变张量的关系比弹性材料要复杂。但是为了寻找6个独立应变分量与6个独立应力分量的关系，可简化为偏应变张量与偏应力张量之间的关系。根据弹性力学理论，可直接写出三维条件下流微分本构形式为

(19)

式中，eij为偏应变张量；σii为应力；δii为应变；K为体积模量；G为剪切模量。

综上分析，对于简单的元件组合模型，可采用单轴蠕变试验参数确定其参数。孙钧[15]认为，在三维应力状态下，蠕变模型很难用形象具体的元件去描述，但三维蠕变本构方程可以采用类比法通过一维蠕变本构方程推导得出，从一维模型到三维模型，只需要将下列的符号对应：σ→Sij、ε→eij、E→G、β→η，则非线性Bingham模型的三维形式为

(20)

exp(tλ)(Sij>σs)

(21)

(22)

2 模型的适用性验证

2.1 岩石蠕变试验曲线

为验证模型的适用性，杨彩虹等[16]采用辽宁工程技术大学能源与新技术研究所自主研制的三轴渗透仪进行了岩石蠕变试验。天然页岩单轴压缩蠕变试验曲线见图4。从图4可以看出，应力水平较低且小于38 MPa时，该模型只发生衰减蠕变和等速蠕变；应力水平大于38 MPa且作用的时间足够长时，该模型会发生衰减蠕变、等速蠕变以及加速蠕变。因此，该试验能够模拟岩石完整蠕变过程，且当应力水平越大时，进入到加速蠕变阶段所需时间越短。

图4 不同应力水平下天然页岩蠕变

2.2 本构模型的参数确定

1stOpt为目前世界领先的非线性曲线拟合及综合优化分析计算软件，该软件在曲线拟合、非线性复杂模型参数估算求解等领域居世界领先地位。通用全局优化算法(UGO)是1stOpt内置的一种线性优化控制算法，该算法最大特点是克服了当今世界上在优化计算领域中使用迭代法必须给出合适初始值的难题，即用户勿需给出参数初始值，而由1stOpt随机给出，通过其独特的全局优化算法最终找出最优解。本以天然页岩蠕变试验为依据，给出了求解粘弹塑性模型参数的方法[17]。

(1)在低应力状态下，即σ≤σs，此时的本构模型退化为2个Hooke体串联，蠕变方程为式(14)。具体的求解方法是：先求解瞬时弹性模量E1，当t=0时，E1=σ0/ε，其中，ε为天然页岩的瞬时形变量，由图4蠕变曲线得出，由于σ0已知即可求得；再通过1stopt软件，通过对试验数据的拟合求得弹性模量E2以及蠕变参数α。

(2)在高应力状态下，即σ>σs，单轴压缩拟合蠕变方程为式(15)，三轴压缩拟合蠕变方程为式(21)。通过输入数据并绘制散点图，自定义函数进行非线性拟合。运用全局优化算法对提出改进后模型蠕变方程的参数进行求取以及模型的适用性验证。程序运行完成即可得到粘滞系数η1与蠕变指数λ，5个流变参数全部求得。各流变参数值见表1。从表1中可以看出，在不同的应力水平下试验数据与拟合曲线的相关系数均达到0.9以上。因此，该模型能够较好地描述岩石蠕变的3个阶段，证明了该模型的适用性。

表1 非线性Bingham模型岩石蠕变参数

蒋海飞等采用RLW-2000岩石三轴流变试验系统，对取自重庆某深基坑细砂岩进行三轴蠕变试验。该岩石的单轴抗压强度为63.40 MPa。蠕变试验设计有2种加载工况，见表2。选取1号试件在高于屈服应力水平下的相关试验和数据，对本文提出的本构方程式(21)进行拟合和模型参数的求取。三轴条件下的砂岩应变曲线的拟合参数见表3。拟合曲线见图5。

表2 三轴蠕变试验工况

注：1号试件自然干燥。

2.3 非线性参数影响分析

从非线性模型的拟合曲线选取3种蠕变曲线代表曲线(见图6)以及表1的参数反演可得，在应力水平未达到开关阀值，且当α越小时，在相同时间内，蠕变变形量和蠕变速率越大，而且进入到稳态蠕变阶段的时间延长，同时衰减蠕变的曲率半径越大；当应力水平达到开关阀值时，通过分析41、45、55 MPa与65 MPa数据曲线可知，随着λ的增大，岩石经历加速蠕变阶段的时间缩短，且在相同时间内，蠕变变形量和蠕变速率也越大。λ的值与岩石非线性加速有很大关系，这也说明了本文考虑这2个系数对岩石蠕变过程的必要性与合理性。

表3 砂岩应变曲线的拟合参数

图5 拟合曲线

图6 不同应力状态下拟合曲线

比较页岩和砂岩在加速蠕变阶段的拟合值发现，砂岩的蠕变指数λ较页岩高1个数量级，可能参数λ的大小与岩石种类以及受到的荷载有关，具体的变化规律需进一步研究确定。

从图5、6可知，试验数据与拟合曲线两者吻合效果良好，特别在高应力状态下拟合的相关系数R2接近于1，因此基于改进的Binghan模型所建立的本构方程能较好地描述静力荷载下岩石蠕变规律。

3 结 语

本文基于传统的Bingham模型，将其模型中的常值牛顿粘体替换为与时间相关的非常值元件并串联一个非线性弹性元件，建立了基于静力荷载下非线性Bingham模型，得出下以结论 ：

(1)与传统的Bingham模型相比，改进后的非线性模型能够较好地模拟岩石的衰减蠕变与加速蠕变阶段，且该模型参数较少，模型简单方便用于工程实际。

(2)基于改进后的Bingham模型所推导的流变本构方程对页岩与砂岩的试验数据拟合表明，所建立的本构方程能较好地描述岩石蠕变整个阶段，尤其是加速蠕变阶段，拟合曲线与试验数据的相关系数R2均在0.9以上。因此，与传统的流变模型对比，本文模型更适合描述岩石材料的流变性质。

(3)通过对控制衰减蠕变系数α与加速蠕变系数λ进行参数分析，α随应力水平增大而减小，且α越小，衰减蠕变的时间越长；λ随应力水平增大而增大，且λ越大，岩石在加速蠕变阶段的蠕变速度越大。