面向海洋应用的低真空质谱仪操作模式研究
2019-11-22姜佩贺穆鹏华王中训赵占锋
姜佩贺,穆鹏华,王中训,赵占锋
(1.烟台大学光电信息科学技术学院,山东 烟台 264005;2.哈尔滨工业大学(威海)信息与电气工程学院,山东 威海 264209)
物质的成分分析是海洋信息感知系统的重要组成部分。质谱仪作为一种根据离子的质荷比进行物质成分鉴定和结构分析的仪器,广泛应用于海洋地质学研究[1]、海洋环境监测[2-3]、海洋污染物检测[4-5]等领域。
对于大多数质谱仪,质量分析需要真空环境。当使用四极杆(四极滤质器)作为质量分析器时,真空腔内的压强需维持在10-5~10-3Pa量级[6]。相对而言,离子阱可工作于较高的压强环境,真空腔内的压强一般维持在10-3~10-1Pa量级[7-9]。为了获取真空环境,一台质谱仪必须配备由涡轮分子泵和机械泵构成的二级真空系统,并长时间运转,因此,真空系统成为质谱仪中最笨重、最昂贵、最消耗能源的部件。使用单个机械泵可以获得一级真空环境,在此环境下进行质量分析可以省掉质谱仪中体积庞大且价格昂贵的分子泵,大幅度降低仪器的成本、质量、体积和功耗,使质谱仪从小型化走向便携化,扩展了质谱仪的应用领域,使其能更加广泛地应用于船舶、浮台、水面航行器等需要现场、实时、快速检测的场合。
在传统的高真空质量分析中,离子阱中离子的运动只受电场力的作用;而在低真空环境下,离子的运动将受电场力和背景气体碰撞的双重作用,运动变得复杂。因此,在低真空条件下进行质量分析,需要改变质量分析操作模式。研究表明,在离子阱质量分析中,适当地提高压强有助于离子冷却,从而提高离子捕获效率[10-13]。但当压强进一步提高时,样品离子与背景气体分子的碰撞频率增加、谱峰延展,仪器的分辨率和灵敏度降低[14-16],最终导致质量分析无法完成。在质量分析中,离子的出射方式包括边界不稳定抛出[17]和共振出射[14]。针对共振出射,Xu等[16]通过理论分析推导了谱峰半峰宽与压强的关系,预测了当压强增大时谱峰发生延展。当使用矩形离子阱(rectilinear ion trap, RIT)作为质量分析器,压强为33.25 Pa时,m/z195.1的谱峰半峰宽约为9.5 u,发现增大射频电压频率可以补偿由于压强增大所造成的谱峰延展。Song等[15]对此进行实验验证的结果与理论分析相符。该研究仅针对共振出射展开,并没有给出使用边界不稳定抛出方式时的相关结论和可用于低真空的质量分析操作模式。
为研究低真空质量分析操作模式,本工作针对圆柱形离子阱(cylindrical ion trap, CIT)离子阱质量分析,基于Langevin碰撞理论,拟在多物理场仿真软件COMSOL Multiphysics 5.2中搭建仿真平台,通过仿真探究低真空环境下离子出射方式为边界不稳定抛出时,射频电压频率、射频电压零峰值、离子阱尺寸等操作参数对仪器灵敏度和分辨率的影响,最终实现低真空质量分析。
1 理论建模
COMSOL Multiphysics中拥有大量的预定义应用模块,本研究选用电流模块(electric currents, ec)和带电粒子追踪模块(charged particle tracing, cpt)进行建模仿真,其中ec模块用于计算交变电场,将计算结果与cpt模块耦合,实现对在电场和碰撞双重作用下离子运动的仿真。
1.1 CIT与四极电场
CIT的整体结构为圆柱体,在COMSOL中使用“圆柱体”对CIT建模,圆柱体侧表面表征CIT的环电极,上下截面分别表征CIT的2个端电极。圆柱体内径为2r0,高度为2z0,其中z0=0.897×r0。在圆柱体的上下表面分别设有直径为2 mm的小孔,表征端电极上用于电子入射和离子出射的小孔。将整个圆柱体区域设置为求解区域,设定圆柱体内部材料电导率σ=0,相对介电常数ε=1。当r0=10 mm,z0=0.897×r0=8.97 mm时,建立的CIT几何模型示于图1。

图1 创建的CIT几何结构模型Fig.1 Geometric structure model of the cylindrical ion trap
1.2 离子的释放与碰撞
应用cpt模块实现离子释放与碰撞的仿真。仿真的样品电离方式为EI源内电离,即具有一定能量的电子从端电极上的小孔入射到离子阱,在阱内与样品碰撞实现样品的电离。因此,待分析离子应在离子阱的中心区域释放。在EI源中,一般将推斥极电压设定为70 V,逸出的电子最初具有70 eV的能量,但在低真空条件下,电子能量会骤减,与样品的碰撞过程中会有一定的能量损失,因此假定电离后的离子具有5 eV的初始能量。
在离子阱的中心区域划定截面半径为2 mm,长度为10 mm的圆柱形作为离子释放区域。离子在0 ms释放,质量为mi,电荷数为1,初速度沿z方向,大小为vz0;设置离子的初始位置为“基于网络”,细化因子为1,即在释放区域的每个剖分网格上均有1个离子释放;设定“壁条件”为“冻结”,即离子碰撞到离子阱内壁后不发生反射,冻结在壁表面。
离子在电场的作用下运动并不断地与背景气体发生碰撞,忽略离子之间的相互作用。使用“碰撞”节点以及“弹性”子节点对该碰撞进行建模。由于背景气体分子的运动速度远小于在电场作用下高速运动的带电离子,因此假定背景气体分子静止,质量为mg,分子密度数为Nd,Nd与压强p的关系为:
(1)
其中,NA为阿佛加德罗常数,R为气体常数,T为绝对温度。
对于Langevin碰撞模型,当离子与背景气体分子相互靠近时,在带电离子的作用下,气体分子内部产生一个诱导偶极,离子与产生的诱导偶极发生库仑作用。当靠近到一定距离时,两者发生能量交换,完成一次碰撞,碰撞截面积为:
(2)
其中,q为离子所带电荷量,ε0为真空中的介电常数,v为离子和背景气体分子的相对速度,αe为气体分子极化率,μ为约化质量(reduced mass)。
离子与背景气体分子的碰撞概率为:
P=Ndσv
(3)
联立式(1)、(2)、(3)得:
(4)
其中,k为玻尔兹曼常数,在数值上k=R/NA。
对于某一个离子,可以根据P′值的大小,判定其在一个仿真步长Δt内是否发生碰撞。方法为在0~1之间取1个随机数,如果P′值大于该随机数,则碰撞发生,反之碰撞不发生。其中P′的表达式为:
P′=1-e-pΔt
(5)
此外,认为离子与背景气体分子的碰撞是弹性的,因此,每次碰撞后离子速度的损失率为:
(6)
2 仿真结果与讨论
在离子阱质量分析中,边界不稳定抛出所使用的质量扫描线是a=0,示于图2。按照质量扫描线,保持U=0,即a=0,增大射频电压零峰值V,离子工作点所对应的q值会逐渐增大,当达到稳定区的边界值0.908时,离子运动会由稳定变为不稳定。马修参数a和q的表达式分别为:
其中,m为离子质量,e为离子所带电量,U为射频电压的直流分量,V为射频电压交流分量的零峰值,ω为射频电压的频率,r0和z0分别为离子阱在r和z方向的半径。
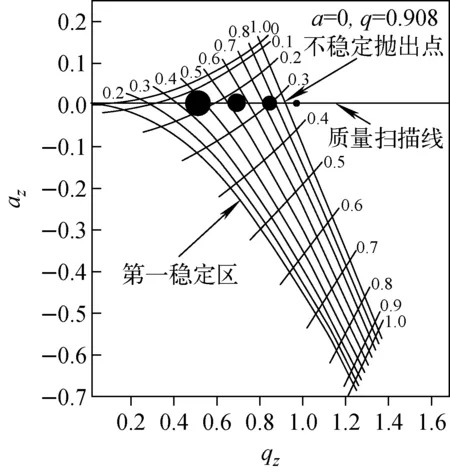
图2 第一稳定区与质量扫描线Fig.2 First stability and mass operating line
离子透射率是指通过端电极上的小孔弹射出阱的离子数量与离子总数量的比值。透射率的大小反映了谱峰的信号强度,而信号强度决定了仪器的灵敏度。在相同条件下,透射率越大,仪器灵敏度越高。离子透射率对时间的微分是单位时间内弹射出阱的离子数量,因此,使透射率达到稳定的时长越短,表明谱峰宽度越窄,即仪器分辨率越高。
由q值的表达式可知,q除了与离子的固有属性m/e有关外,还与ω、V以及r0有关(z0与r0成比例,z0=0.897×r0),由此,为了达到离子的不稳定抛出点0.908,ω、V以及r0可以有不同的组合。在以下的仿真中,将保持马修参数(a,q)=(0, 0.95)这一离子不稳定运动条件不变,通过改变3个参数中的2个,从谱峰宽度和强度,即质谱仪的灵敏度和分辨率两个角度探寻低真空下的质量分析方法,其它仿真参数列于表1。

表1 仿真参数Table 1 Simulation parameters
2.1 射频电压频率与射频电压零峰值
射频电压频率ω是质量分析中的一个重要参数,它决定了四极场的固有属性。在q值表达式中,ω的单位是rad/s,但在实际实验中,为方便表述,射频电压频率一般使用单位为Hz的变量f描述,二者在数值上具有2π倍的关系。
设置离子阱尺寸r0为5 mm,改变射频电压频率ω,同时改变射频电压零峰值V,以保证q=0.95不变,不同参数下的离子透射率示于图3。
仿真结果表明,射频电压频率越高,透射率到达稳定的时长越短,稳定后的透射率越大。当射频电压频率为1 MHz时,透射率达到稳定的时长约为9 μs,稳定的离子透射率约为0.14;而当射频电压频率为4 MHz时,透射率 达到稳定的时长约为1.8 μs,稳定的离子透射率约为0.78。

图3 不同射频电压频率ω和电压零峰值V下的离子透射率Fig.3 Transmission probability in different frequency and amplitude of RF voltage
不同频率下,仿真结束时刻离子的运动状态示于图4,图中的颜色表示离子的运动速度。图4a的仿真条件是ω=0.5 MHz,由于射频电压频率过低,离子碰撞能力差,被聚焦在离子阱的中心区域,离子透射率为0;图4b和4c的仿真频率分别为1 MHz和3 MHz,随着射频电压频率的提高,离子的动能越来越大,能够透过端电极小孔的离子数量越来越多,因此获得了更高的透射率;图4d的仿真条件是ω=5 MHz,此时,离子基本全部透过端电极上的小孔。
由四极场理论可知,当前(a,q)值位于稳定区外部,离子运动是不稳定的,但当背景气体压强提高,离子与背景气体发生碰撞,不同的射频电压频率得到了不同的离子运动状态,低频率下,碰撞导致了大多数离子运动稳定,与理论分析不符。当频率增大,不稳定运动的离子数量才逐渐增多。

注:a.ω=0.5 MHz;b.ω=1.0 MHz;c.ω=3.0 MHz;d.ω=5 MHz图4 不同射频电压频率ω和电压零峰值V下,离子在仿真结束时刻的运动状态Fig.4 Ion states at the end of the simulation in different frequency and amplitude of RF voltage
2.2 射频电压频率与离子阱尺寸
改变射频电压频率ω后,为保证q值不变,一种方法是如2.1节所述,改变射频电压零峰值V,另一种方法是改变离子阱尺寸r0。设置射频电压零峰值V为127 V,在改变射频电压频率ω的同时改变离子阱尺寸r0。不同参数下的离子透射率示于图5。

图5 不同射频电压频率ω和离子阱尺寸r0下的离子透射率Fig.5 Transmission probability in different frequency of RF voltage and r0
仿真结果与2.1节类似,使用高频率的射频电压可以获得更大的离子透射率和更短的透射率稳定时间。当射频电压频率为1 MHz时,透射率达到稳定的时长约为8.4 μs,稳定后的离子透射率约为0.09;而当射频电压频率为4 MHz时,透射率达到稳定的时长约为2.1 μs,稳定的离子透射率约为0.45。
由2.1节和2.2节可以得出:使用高频率的射频电压可以获得更窄的谱峰宽度和更强的谱峰信号,使仪器拥有更高的灵敏度和分辨率。这是因为增大射频电压频率,离子在单位时间内从四极场中获取了更多的能量,使其运动速度增大,碰撞能力增强。
2.3 离子阱尺寸与射频电压零峰值
设置射频电压频率ω为1 MHz,改变离子阱尺寸r0,保持z0=0.897×r0,同时改变射频电压零峰值V,以保证q=0.95不变。不同条件下的离子透射率示于图6。仿真结果表明,当离子阱尺寸r0不同时,透射率达到稳定的时长基本一致,在仿真结束时刻,透射率均保持在0.15附近,并没有因为离子阱尺寸的变化而发生明显改变,因此单纯地改变离子阱尺寸不会改善低真空质量分析性能。
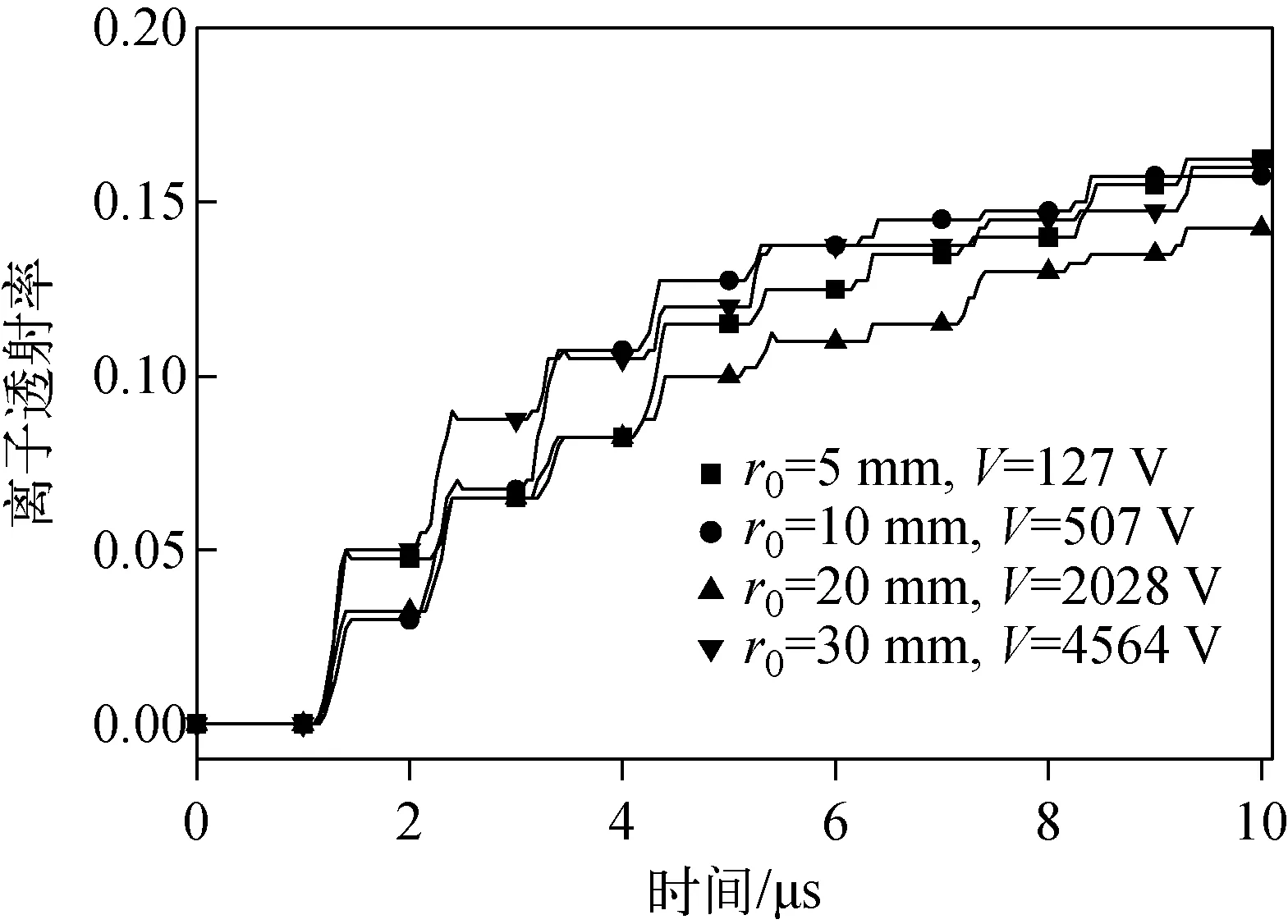
图6 不同离子阱尺寸r0和射频电压零峰值V下的离子透射率Fig.6 Transmission probability in different dimensions of CIT and amplitude of RF voltage
由2.1节和2.2节的分析可知,提高射频电压频率会改善谱峰信号强度和谱峰宽度。根据q的表达式,当射频电压频率提高,为达到用于质量分析的q值,只能成平方关系的提高V值或等比例的减小r0。射频电压零峰值V由硬件电路决定,难以大幅度提高,且高电压容易引起放电。因此,从该角度分析,为能够使用更高频率的射频电压,必须减小离子阱的尺寸r0。
3 结论
在低真空环境下进行质量分析可以大幅降低质谱仪的成本、体积和功耗,是实现质谱仪从小型化到便携化的重要策略之一。针对低真空环境下的质量分析,通过仿真,从谱峰宽度和强度,即质谱仪的灵敏度和分辨率两个角度探寻了CIT质谱仪在低真空下的质量分析操作模式。结果表明,从q值的表达式看,在增大射频电压频率的同时减小离子阱尺寸,可以最大限度的平衡由于压强变化所引起的仪器性能的降低。
