外缘凸起对离合器温度场的影响研究

王 超 程 铖 陈 俐

(上海交通大学海洋工程国家重点实验室， 高新船舶与深海开发装备协同创新中心，上海 200240)

0 引言

离合器在短时间内产生大量摩擦热的极端工况为爬行起步和频繁换挡[4,5,6]。文献[7]从运行工况的角度进行分析，指出滑摩转速、摩擦力矩以及滑摩时间是影响温升的关键因素。文献[8]研究表明一次起步过程中离合器温度上升30～35 ℃，反复几次则可上升20～300 ℃，这时导致摩擦系数明显下降。文献[9]建模比较了离合器摩擦界面压力均布与热流密度均布两种假设下温度场分布的区别。

上述研究假设离合器压盘为圆环结构，其内外径分别与摩擦片相当。而工程上为了传递发动机的动力，一般在压盘外缘设计若干凸起，在凸起上通过铆钉或螺纹连接发动机飞轮盘，如图1所示。该凸起结构的表面不接触摩擦片，不产生摩擦热，但是增加了压盘质量，因而增大了热容量，而且几何结构上类似肋片，可一定程度强化压盘的散热。本文建立具有凸起结构的压盘模型，分析凸起结构的分布形式及尺寸对离合器的最高温度以及温度分布的影响，弥补传统设计仅关注压盘强度的不足，为新型结构设计与优化提供参考。

本文在ANSYS软件中建立三维有限元瞬态传热模型，模型的有效性通过台架试验数据验证，然后比较不同的凸起分布与凸起尺寸时，离合器最高温度、径向与周向温度分布特征的变化规律。

2 离合器瞬态传热模型

本节分析干式离合器的传热路径，建立导热微分方程式，并给出边界条件和初始条件。

2.1 导热微分方程

干式离合器由摩擦片、压盘和驱动盘三个部件组成。摩擦片有两个摩擦面，分别与压盘和驱动盘相对。当它们接触并有相对滑摩转速时，摩擦界面上产生摩擦热。摩擦热的传热路径如图1所示，热量通过热传导传递到摩擦片、压盘和驱动盘内部，三个部件的表面以对流换热的方式散热至周围空气。因离合器温度一般不超过400 ℃，辐射传热量很小，热分析中将其忽略。

2010年6月，辽宁农业职业技术学院园林系与营口某高尔夫俱乐部签订协议，共同培养高尔夫球运动与管理专业学生，从2010级到2015级共六届高尔夫球运动与管理专业学生都采用了“校企一体”教学模式。

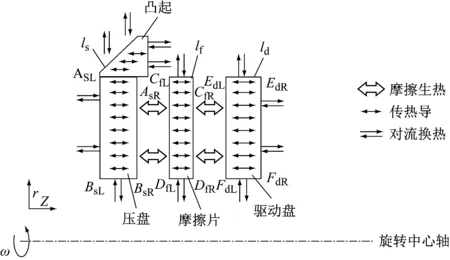
图1 离合器摩擦热的传热路径Fig.1 Heat transfer paths of friction heat of clutch

为了便于计算与分析，本文假设摩擦片、压盘和驱动盘的物性参数各向同性，且忽略各部件的热变形。考虑各部件基本上为圆盘形状，在柱坐标系(r,θ,z)中推导导热微分方程。摩擦片、压盘和驱动盘的导热微分方程分别表示如下：

(1)

(2)

(3)

其中，下标s、f、d分别表示压盘、摩擦片和驱动盘。τs(rs,θs,z,t) 、τf(rf,θf,z,t)、τd(rd,θd,z,t)分别为压盘、摩擦片和驱动盘的温度，ρi、ci、λi(i=s,f,d)分别表示密度、比热容和导热系数。

2.2 边界条件

按照表面是否产生摩擦热量，压盘、摩擦片和驱动盘的表面可以分成两部分，即摩擦生热面和散热面。为了表达方便，如图1中，摩擦生热面为AsRBsR、CfLDfL、CfRDfR、EdLFdL，ls表示压盘上圆筒壁散热面(即内径圆筒壁面和外径圆筒壁面)，lf表示摩擦片上的圆筒壁散热面(即内径圆筒壁面与外径圆筒壁面)，ld表示驱动盘上的圆筒壁散热面(即内径圆筒壁面和外径圆筒壁面)。

以压盘为例，摩擦生热面的边界条件表示为：

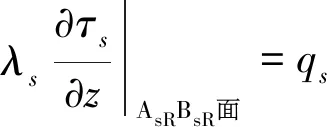
(4)

其中，qs为AB面上的摩擦热流密度。

散热面的对流换热边界条件为：

(5)

(6)

其中hs为散热面的对流换热系数，τ∞为环境温度。

类似的，摩擦片的摩擦生热面与对流换热面的边界条件分别为：

(7)

(8)

(9)

其中，qf_1、qf_2分别为CfLDfL面和CfRDfR面上的摩擦热流密度，hf为对流换热系数。

驱动盘的摩擦生热面与对流换热面的边界条件分别为：

(10)

(11)

(12)

其中，qd为GH面上的摩擦热流密度，hd为对流换热系数。

摩擦热流密度qs、qf_1、qf_2与qd将在后面进行推导。

2.3 初始条件

初始温度条件描述如下：

τ(ri,θi,zi,t)|t=0=τ0(ri,θi,zi) (i=s,f,d)

(13)

其中，τ0是离合器的初始温度。

2.4 摩擦热流密度模型

从图1可知，一组离合器中有两个摩擦界面，即AsRBsR-CfLDfL界面和CfRDfR-EdLFdL界面。以AsRBsR-CfLDfL界面为例，令摩擦系数为μ，摩擦表面上的单位面积压力为σ，滑摩转速差为Δω，摩擦片外径为R2、内径为R1，在任意半径R处的摩擦热流密度q1为：

q1=μ(τ)·σ(t)·Δω(t)·R

(14)

摩擦表面上的单位面积压力σ由下式计算得出：

(15)

其中，Fn为作用在摩擦面上总的正压力。

将式(15)代入式(14)得到热流密度的计算公式如下：

(16)

上式中，Fn(t)、Δω(t)是时间t的函数，取决于运行工况；此外，试验中发现摩擦系数μ(τ)受到温度τ的显著影响，模型μ(τ)通过实验获得。

热流密度q1在摩擦界面AsRBsR-CfLDfL上产生，将分别通过AsRBsR面和CfLDfL面向压盘和摩擦片逐渐传递，基于能量守恒原理，存在如下能量平衡式：

qs+qf_1=q1

(17)

至于qs和qf_1的分配，常用的固定比例的分配方法[5,18,19]导致摩擦界面附近温度场不连续，不符合物理实际。本文在ANSYS软件中进行建模，在摩擦界面上设置“glue”功能，可基于能量守恒原理自动动态分配公式(17)中的qs和qf_1，计算结果在摩擦界面附近温度场连续，符合实际情况。

类似地，令摩擦界面CfRDfR-EdLFdL上的热流密度为q2，计算式与式(16)相同，且存在：

qd+qf_2=q2

(18)

其中，qd和qf_2的大小通过设置“glue”功能基于能量守恒原理进行分配。

3 仿真结果与讨论

基于前一节建立的有限元热分析模型，本节给出了数值计算结果。为了比较，本节也给出未考虑凸起结构的有限元模型计算结果。首先比较有凸起结构的离合器模型与传统的无凸起结构的离合器模型的计算结果，比较压盘摩擦面和圆周截面的温度分布与温度梯度分布；然后，给出不同尺寸和不同分布的凸起结构的计算结果，分析凸起尺寸与分布对温度场的影响。

仿真工况为：正压力275 N，滑摩转速800 rpm，传统的无凸起模型的计算结果如图2(a), 温度沿着径向和高度方向变化，而在圆周方向上没有变化。本文考虑凸起结构的模型计算结果如图2(b)，温度不但沿着径向和高度方向变化，而且在圆周方向也发生变化。基本上，由于凸起结构对热量的散发与吸收作用，靠近凸起处，温度较低，而远离凸起处，温度较高。

由于摩擦界面在离合器结构的内部，图2中显示不出摩擦界面的温度场，图3-图13给出压盘摩擦面以及圆周截面的温度场分布的比较。

(a) 传统的无凸起模型

(b) 有凸起的模型

图2 离合器温度场云图比较

Fig.2 Comparison of temperature images of clutch

(a1) t=1 s(b1) t=1 s

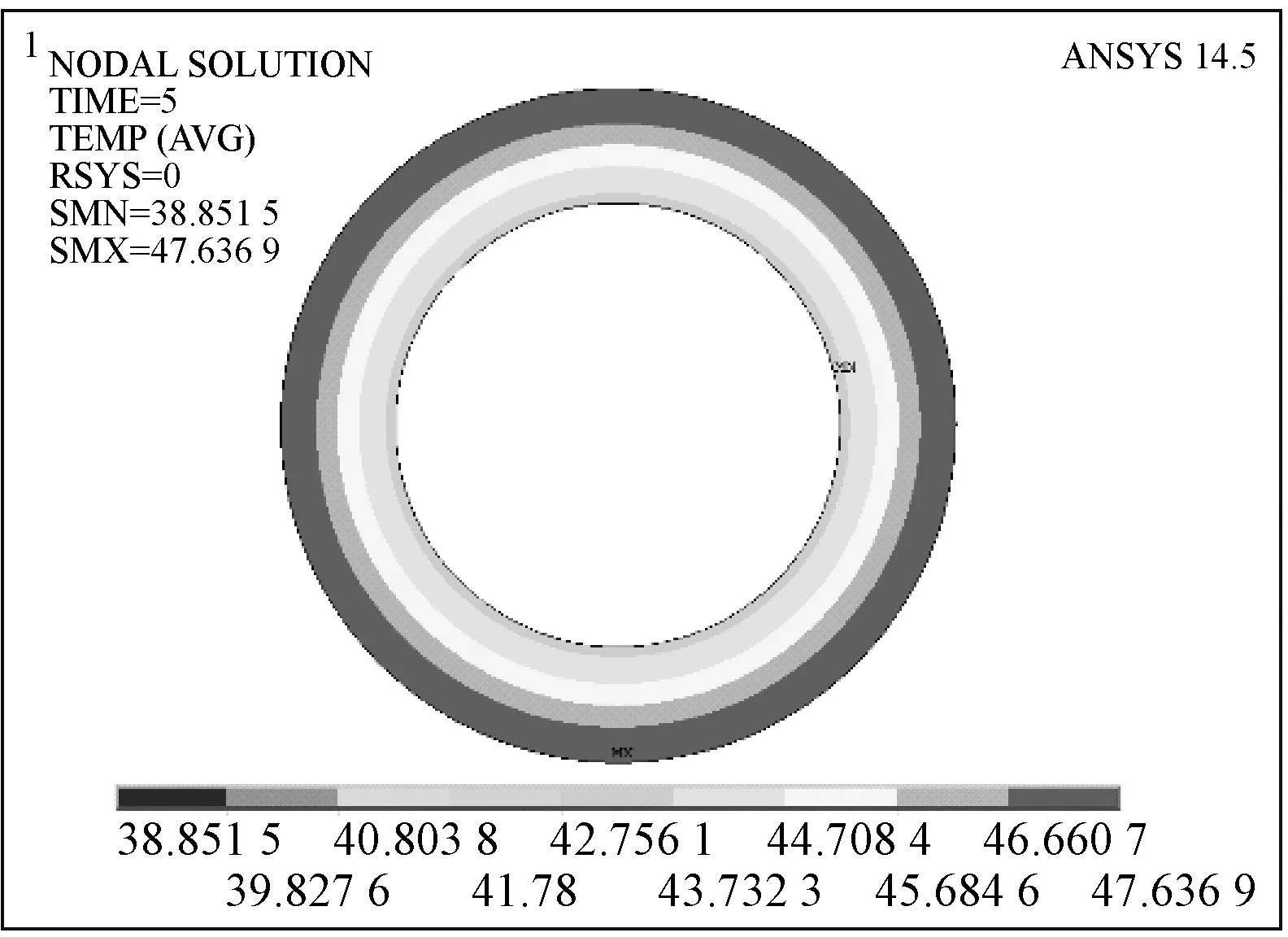
(a2) t=5 s(b2) t=5 s

(a3) t=20 s(b3) t=20 s

图3 压盘摩擦面温度云图比较

Fig.3 Comparison of temperature images of pressure plate friction surface

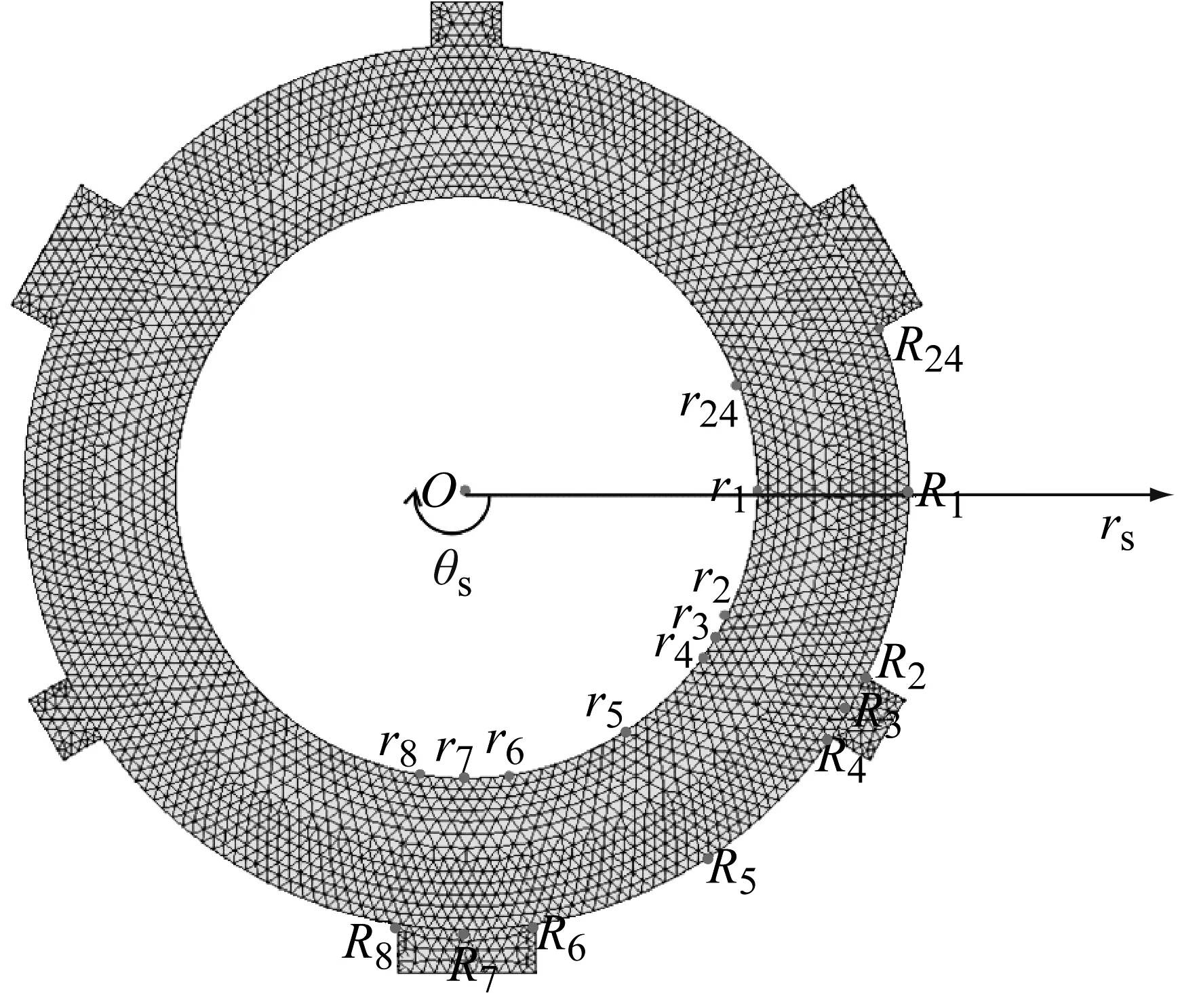
图4 周向取点示意图Fig.4 Diagram of circumferential fetching

为了进一步探究凸起结构对温度场的影响，对有无凸起压盘的截面温度场进行研究，如图5，取出有凸起结构压盘的截面A及截面B与无凸起结构压盘的任一截面进行对比。

图7是工况为正压力275 N，滑摩转速差为800 rpm，运行一段时间的有凸起结构离合器其两个径向截面的瞬态温度云图与无凸起结构压盘任一截面的对比。

4 结论

本文针对一套干式DCT，通过有限元仿真与实验验证的方法研究了凸起结构对离合器温度场的影响，研究结果表明：(1)凸起结构能一定程度降低压盘的温度，但是会增大温度梯度，从而增大热应力，并且凸起尺寸越大，其效果越明显；(2)最高温度点发生在截面B靠近外径处；(3)径向方向上，凸起对截面A的温度分布影响显著，对截面B则影响不大；(4)周向方向上，凸起对外径的温度场影响大于对内径的，且凸起的存在使周向上的温度场分布为周期性的。

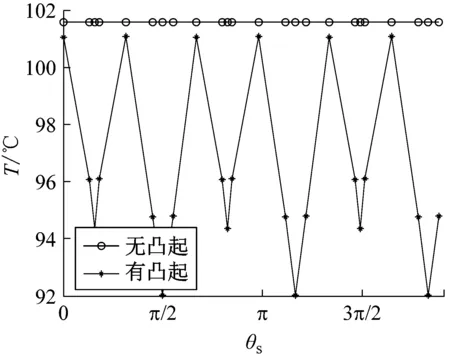
(a) 外径处温度分布

(b) 外径处温度梯度分布图5 压盘周向的温度与温度梯度(t=40 s，rs=102.5 mm)

Fig.5 Circumferential Temperature and temperature gradient of the press plate(t=40 s，rs=102.5 mm)

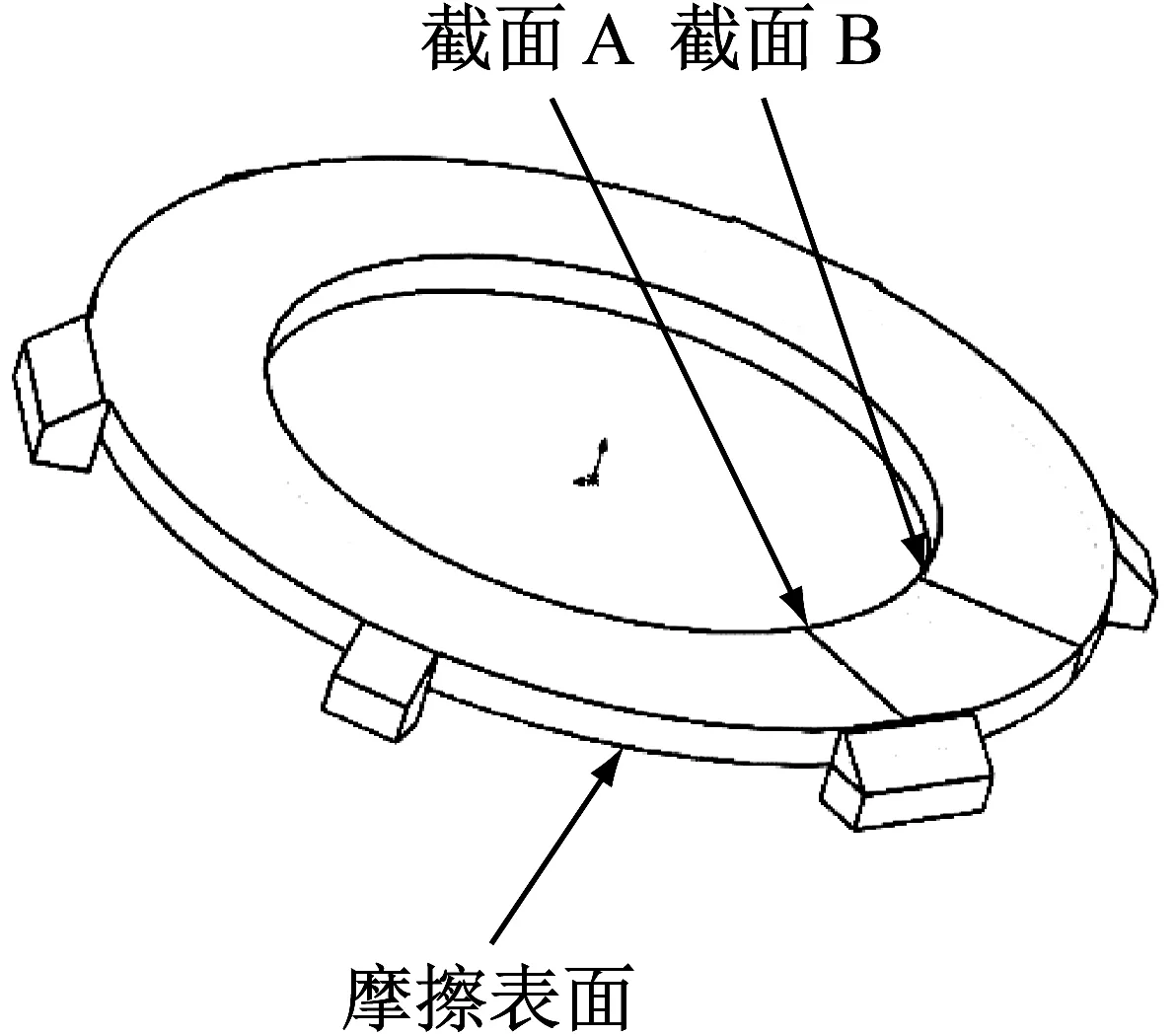
图6 压盘的两个截面示意图Fig.6 Diagram of two sections of a pressure plate

图7 压盘截面温度云图比较

Fig.7 Comparison of temperature images of pressure plate cross section

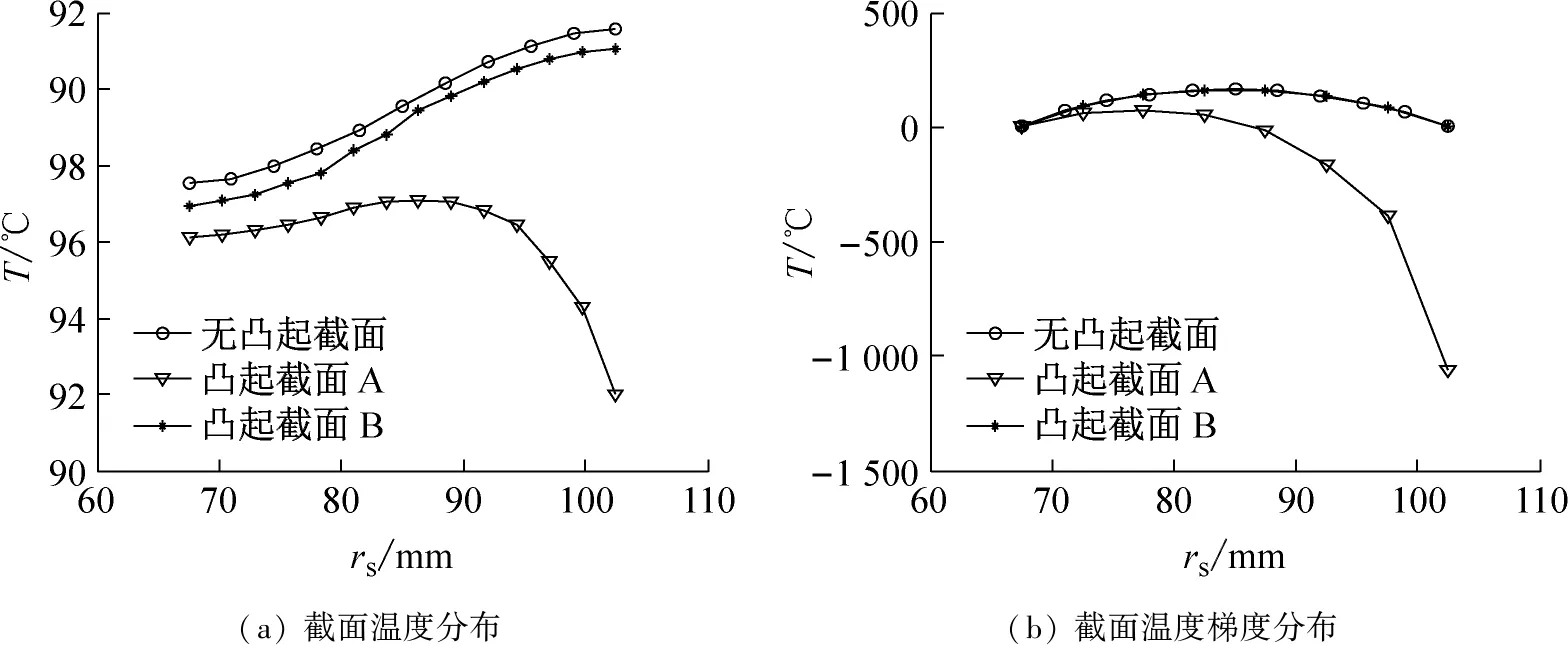
图8 压盘径向温度与温度梯度(t=40 s)Fig.8 Radial temperature and temperature gradient of pressure plate(t=40 s)