基于AMESim的电机扭矩在线估算动态模型研究

朱福堂 王洋洋 鲁 超

(比亚迪汽车工业有限公司 产品规划及汽车新技术研究院， 广东 深圳 518000)

1 引言

动力系统作为新能源汽车最重要的核心系统，其主要包括电机、电机控制器和减速器，驱动电机是其动力源，它将电能转化为机械能来驱动汽车行驶。内置式永磁同步电机(IPMSM)以其功率密度高、动态响应快、效率高、调速范围宽等[1-3]优点已经成为新能源汽车主机厂的首选电机。电机扭矩的精准控制对于电机的效率、整车能耗具有较大影响；然而现有实车电机扭矩的估算是基于查表模型，但电机在工作一段时间后电机内特性参数就会发生变化，比如退磁现象及电机老化等，此时再通过查表估算电机扭矩就会造成较大误差，因此研究电机扭矩在线估算具有重要的理论意义和工程意义。

2 电机扭矩在线估算建模

电机扭矩估算模型包括参数子模型、可调子模型和自适应子模型，如下图1所示，在自适应子模型估算出的电机内特性参数基础之上对电机扭矩进行计算估计[4-5]。

图1 电机扭矩在线估算框图Fig.1 Motor torque online estimation diagram

2.1 参考子模型建模

参考子模型采用的是新能源汽车电机电控系统最常用控制算法，即最大转矩电流比控制(MTPA)。电机电控系统在整车上的主要功能为接收VCU的转矩信号，通过一系列转换产生三相交流电使得电机端可以输出相应的转矩。最大转矩电流比控制可以保证电机输出所需扭矩的同时实现电流最小，在id-iq坐标系下其轨迹如图2所示[6-7]。

图2 id-iq坐标系下IPMSM的MTPA曲线Fig.2 MTPA curve of IPMSM in id-iq coordination system

2.1.1 电机数学模型

忽略谐波、铁心饱和、三相电流完全对称及转子无阻尼绕组的前提下，PMSM的d/q轴坐标系下的数学模型为[8-10]：

(1)

式中，ud、uq为定子电压矢量的d轴、q轴分量，id、iq为定子电流矢量的d轴、q轴分量，Rs为定子电阻，φr为永磁体磁链，we为电机电角速度，Ld、Lq为电机定子绕组d、q轴电感。

2.1.2 参考子模型

最大转矩电流比控制是在给定转矩的情况下，通过最优的id/iq使得定子电流最小。对于电动汽车驱动系统而言，逆变器的容量是一定的，采用最大转矩电流比控制，可以使逆变器所需输出电流较小，逆变器功率等级相对较低。基于最大转矩电流比控制的参考子模型如图3所示。参考子模型主要由转矩控制环、电流控制环、Park变换器、反Park变换器、逆变器、电机、角速度传感器、电压传感器等组成。

图3 参考子模型Fig.3 Reference sub-model

2.2 估算模型建模

公式(2)为最常用的电机扭矩计算公式：

(2)

由上式可知，若φr、Ld、Lq、id、iq已知，即可在线估算出电机扭矩。整车控制器内的电压/电流霍尔传感器，可以采集电压/电流信号，经过反Park坐标变换可以得到d/q轴电压/电流。本文研究时先假设永磁体磁链φr为固定值，在日后模型优化时再考虑永磁体磁链的变化。所以，估算模型需要估算出d/q轴电感。现有参数估算方法主要有：模型参考自适应法、最小二乘法、卡尔曼滤波法和智能控制算法[11]，本文采用模型参考自适应法对Ld/Lq电感进行辨识，进而对电机扭矩估算。

将公式(1)转换成公式(3)，如下所示：

(3)

式中：a=1/Ld，b=1/Lq，c=φr/Lq。

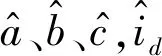
(4)

两式相减可得：

(5)

整理可得：

(6)

令：

(7)

则可写成误差状态方程：

pe=Ae-w

根据Popov超稳性定理[13]，误差e与公式(7)构建成不等式应满足如下条件：

(8)

(9)

进而可求各个参数的自适应律为：

(10)

2.3 结果分析

根据前面的分析与研究，可以搭建电机扭矩在线估算模型，如图5所示。

图5中参考子模型是采用最大转矩电流比控制算法的电机电控系统，可调子模型和自适应模型实现对电机参数的辨识，最后基于辨识出的电机参数计算电机扭矩，从而实现了对电机扭矩的估算。其中，电机电控系统包括电机和电控，电机是指永磁同步电机，电控是指控制信号和逆变器，工作时电控通过信号控制逆变器六桥臂的开通和关断，从而实现对交流电幅值和频率的控制。

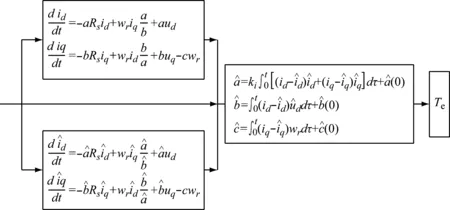
图4 辨识原理图Fig.4 Schematic diagram of parameter identification

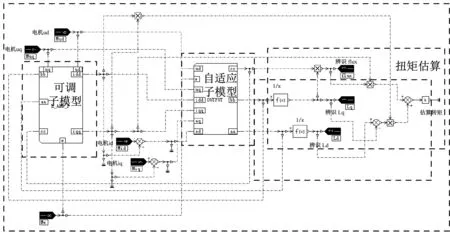
图5 电机扭矩估算AMESim模型Fig.5 AMESim model for motor torque estimation

模型中所用的电机内特性参数具体数值如表1所示。

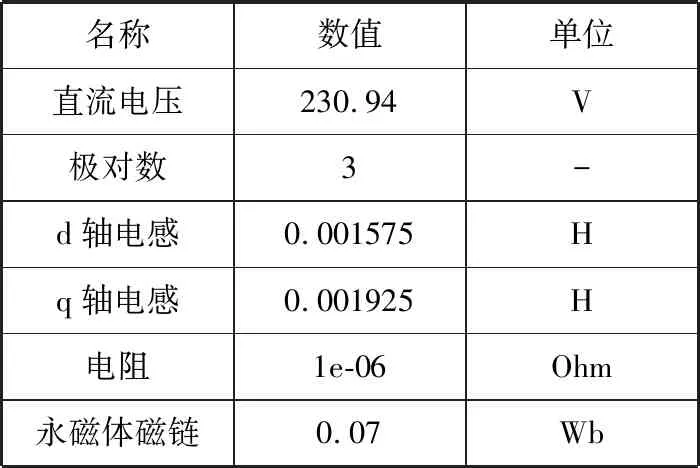
表1 电机参数

根据所搭建的电机扭矩估算模型及参数设置进行仿真分析，其参数估算结果和扭矩估算结果如图6～图8所示：

从图6中可以看出估算的d轴电感在瞬态时的误差约为7%，稳定后误差约为1% ，误差较小、精度较高。

从图7中可以看出q轴电感估算误差在瞬态时的最大值约为0.3%，稳定后误差接近0，误差可以忽略不计，精度较高。

从图8中可以看出电机扭矩估算误差在瞬态时的最大值约为17%，这是因为电机启动瞬间会经历一个短暂的超调过程；从电机输出扭矩与估算扭矩对比图中可以发现两者数值相差不大，但误差图中显示误差较大，这是因为响应略有延迟导致，稳定后误差约为0%，稳态误差可以忽略。

从以上仿真实验中可以得出该电机扭矩估算在线模型估算误差较小、精度较高。但电机启动瞬态误差略大，需要进一步提高扭矩估算响应速度以优化瞬态误差。

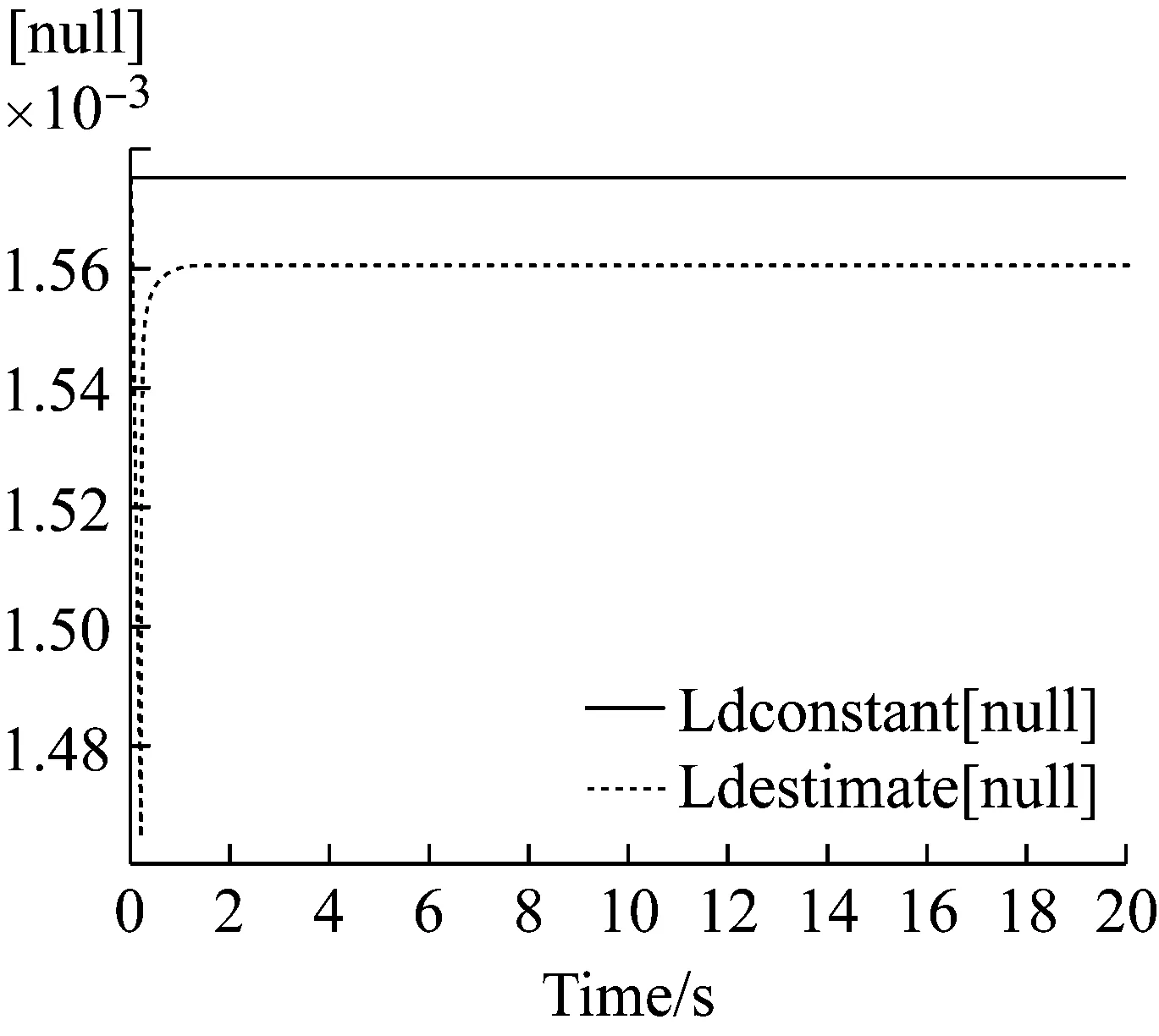
图6 Ld估算与误差图Fig.6 Ld estimation and error diagram

图7 Lq估算与误差图Fig.7 Lq estimation and error diagram

3 整车动态仿真模型

将电机扭矩在线估算模型集成到一级整车动态模型，如图9所示，模型主要包括整车模型、驾驶员模型、电机电控模型、电池模型、减速器以及所搭建的电机扭矩在线估算动态模型。

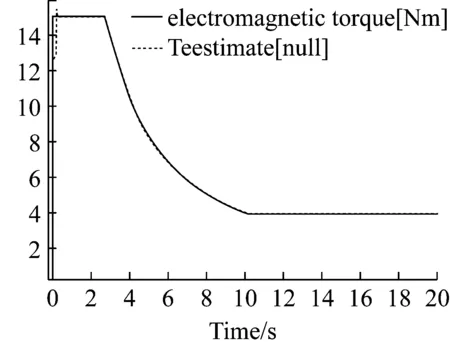
图8 电机输出扭矩与估算扭矩对比和误差图

Fig.8 Comparison and error diagram of motor output torque and estimated torque

图9 整车动态模型Fig.9 Vehicle dynamic model

利用所搭建的电机扭矩在线估算模型在NEDC工况下做模拟仿真，标准车速与车速仿真结果如图10所示，电机扭矩估算结果与扭矩传感器测量结果如图11所示。

从图10 NEDC模型仿真车速和标准工况车速对比图中可以发现两车速追踪效果较好，误差可以忽略，精度较高。

从图11电机扭矩估算结果与扭矩测量结果对比图中可以发现电机估算扭矩与利用扭矩传感器测量的电机扭矩两者曲线追踪效果较好，精度较高、误差小。

图10 NEDC标准工况车速与仿真车速对比

Fig.10 Comparison of NEDC velocity profile and simulated velocity

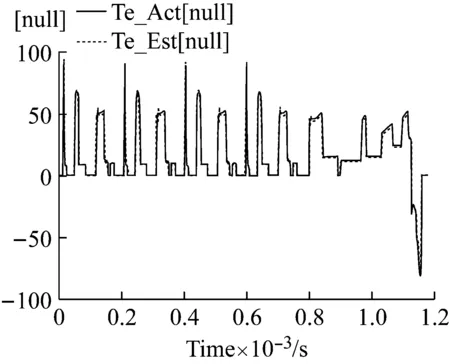
图11 电机扭矩估算结果与扭矩测量结果对比

Fig.11 Comparison of motor measurement torque and estimated torque

4 小结

本文搭建了一种电机扭矩在线估算模型，模型包括参考子模型、可调子模型、自适应子模型，其中参考子模型采用的是最大转矩电流比控制。在介绍电机扭矩在线估算模型搭建过程基础之上，利用AMESim软件进行了仿真验证，得出在仿真开始的瞬态过程误差相对略大，稳定后误差很小，精度较高。最后将该电机扭矩在线估算模型集成于整车模型之中，通过NEDC工况整车动态仿真对比发现电机扭矩在线估算结果与扭矩传感器测量结果相差较小，精度较高。该电机扭矩在线估算动态模型对电机精准控制、策略优化和日后搭载于整车系统的电机扭矩在线估算工程应用具有较强的指导意义。