功率分流式混合动力汽车分析及能量管理策略研究
2019-11-22刘洋肖扬喻凡罗哲
刘 洋 肖 扬 喻 凡 罗 哲
(1.上海交通大学汽车工程研究院底盘所,上海 200240; 2.联合汽车电子有限公司,上海 201206)
0 前言
在纯电动汽车和燃料电池汽车相关技术尚未成熟之前,混合动力汽车(Hybrid Electric Vehicle,HEV)作为一种过渡车型兼顾了燃油车和纯电动汽车的优点,在节能减排方面具有很大潜力[1]。目前的混合动力汽车按照驱动系统的结构分为串联式HEV(Series HEV)、并联式HEV(Parallel HEV)和功率分流式HEV(Power-split HEV)[1][2][11][12]。功率分流式HEV使用机械和电气两个功率耦合器,通过合理的控制能够兼具串联式和并联式HEV的优势,由于结构的复杂性,其能量管理策略成为重要研究内容之一。
文献[2]对目前混合动力汽车能量管理策略进行了详细的分析与总结。目前,大量文献主要以串联式或并联式HEV为对象进行能量管理策略的研究,针对功率分流式HEV的分析和管理策略的研究相对较少[3]。Jinming Liu等针对Pruis结构建立了数学模型,并研究了基于规则(Rule-Based)、基于等效燃油消耗最小(Equivalent Consumption Minimization Strategy, ECMS)和基于随机动态规划(Stochastic Dynamic Programming, SDP)的能量管理策略[3][4]。Dehua Shi等针对提出的功率分流式机构进行建模,制定了工作模式切换逻辑,并基于旁氏最小理论(Pontryagin’s Minimum Principle, PMP)进行了控制策略开发[5]。
混合动力汽车能量管理策略按照控制方式的不同分为基于规则的管理策略和基于优化的管理策略[2]。基于规则的能量管理策略控制简单,相比于基于优化的能量管理策略更加易于实现。本文针对一种特定的双行星排式功率分流机构,对其结构及工作模式进行了分析,并建立了不同工作模式下的运动学方程。基于此制定了工作模式切换逻辑,开发了以发动机为核心的基于规则的能量管理策略。
1 双模式混合动力系统
1.1 双模混合动力系统结构
如图1和2所示,该双模混合动力系统由发动机、电机MG1、电机MG2和两个行星排机构PG1、PG2组成。每个行星排有太阳轮、行星架和齿圈三个节点。电机MG1安装在行星排1的太阳轮上,当车辆功率需求较大时可以作为辅助动力源从蓄电池中获得能量,当车辆需求功率较小时可以作为发电机转化发动机额外的机械能为蓄电池补充电量。电机MG2安装在行星排2的太阳轮上,用来直接驱动车辆,制动时还可以作为制动能量回收装置。发动机安装在行星排1的齿圈上,其所产生的功率通过行星排1进行分流,一部分能量直接传递到输出端驱动车辆行驶,另一部分能量通过发电机MG1转化为电能储存在蓄电池中或者用来驱动电机MG2;两个行星排的行星架固连在一起后作为输出端与主减速器相连接。此外,该混合动力系统中还存在三个离合器B1、C1和OWC1,通过控制离合器的锁止与释放来实现不同工作模式的切换。其中,OWC1为单向离合器,防止发动机出现倒拖。
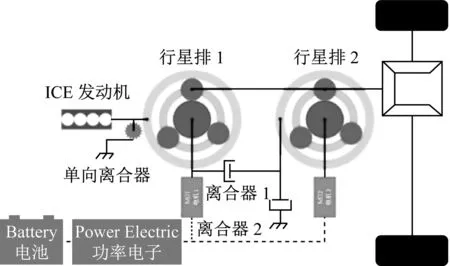
图1 混合动力系统示意图Fig.1 Scheme Diagram of Hybrid System

Engine:发动机 MG1:电机1 MG2:电机2 B1、C1:离合器 OWC1:单向离合器 PG1:行星齿轮组1 PG2:行星齿轮组2
图2 混合动力系统结构图
Fig.2 Structure Diagram of Hybrid System
1.2 双模混合动力系统工作模式分析
由上节所述可知,通过三个离合器的开闭与结合,可以实现不同模式的切换,具体如下表1所示。

表1 不同工作模式下离合器的开闭情况以及各动力源的工作状态(●表示闭合,○表示断开)
1.2.1 纯电动模式1(CD1)
纯电动工作模式1,离合器C1、OWC1断开,离合器B1闭合,由电机MG2单独驱动车辆行驶。该模式下,行星排PG2仅起到固定齿比的减速器作用,行星排PG1没有动力输出,且由于发动机的惯性较大,电机MG1处于倒拖状态,既不发电也不提供动力输出。采用等效杠杆原理[6]得到各动力源的转速转矩关系如下:
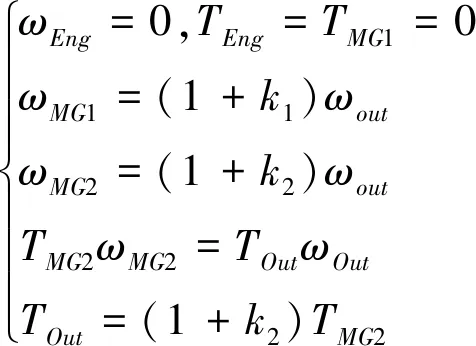
(1)

图3 纯电动模式1等效杠杆图Fig.3 Equivalent Lever Diagram of One Motor EV Mode
1.2.2 纯电动模式2(CD2)
纯电动模式2,离合器B1、OCW1闭合,离合器C1断开,发动机不工作,电动机MG1、MG2同时参与车辆的驱动。此时,行星排PG1、PG2相当于两个减速器并联在一起,电机MG1和MG2的扭矩经过放大后耦合在一起,形成一种转矩耦合结构。各动力源的转速转矩关系如下:

(2)

图4 纯电动模式2等效杠杆图Fig.4 Equivalent Lever Diagram of Two Motor EV Mode
1.2.3 低速增程模式(CS1)
低速增程模式下,离合器B1闭合,离合器OWC1、C1断开,发动机参与驱动。此时整车需求功率较小,且由于发动机在低速、低扭工况下的效率很低,所以需要控制发动机工作在高效区域,发动机产生的机械能一部分通过输出轴与MG2的能量进行汇流后用来驱动车辆行驶,另一部分驱动发电机MG1发电。如图5所示,将MG2等效到C2上则可以发现,该模式实际为输入分流模式。各动力源的转速转矩关系如下:

(3)

图5 低速增程模式等效杠杆图Fig.5 Equivalent Lever Diagram of Low Extended Range Mode
1.2.4 固定速比增程模式(CS2)
固定速比增程模式下,离合器B1、C1闭合,单向离合器OWC1断开,电机MG2和发动机工作,电机MG1由离合器C1锁止,不工作。发动机产生的所有功率全部输出到车轮端,在行星排1上不存在功率分流现象。电机MG2的工作状况视车辆需求而定,当车辆制动时,MG2作为能量回收装置发电;当车辆的功率需求较高时,电机MG2驱动以补充额外的功率需求;当车辆的功率需求较低时,电机MG2通过吸收发动机多余的功率发电,从而调节发动机工作在高效区域。同纯电动模式CD2一样,该模式也为转矩耦合的并联机构。各动力源的转速转矩关系如下:

(4)
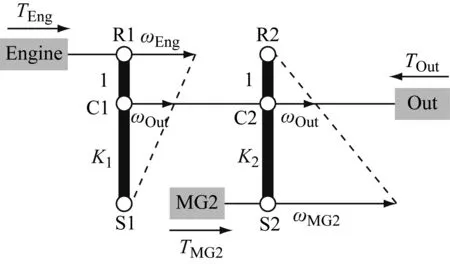
图6 固定速比增程模式等效杠杆图
Fig.6 Equivalent Lever Diagram of Fixed Ratio Extended Range Mode
1.2.5 高速增程模式(CS3)
高速增程模式下,离合器B1、OWC1断开,离合器B1锁止。发动机,电机MG1,电机MG2均参与工作,两个电机是否以电动机或者发电机运行需要视整车的功率需求而定。通过控制电机MG1、MG2来控制发动机的转速和转矩,使得发动机在高效区域内运行。该模式为典型的复合分流模式。各动力源的转速转矩关系式如下:

(5)

图7 高速增程模式等效杠杆图Fig.7 Equivalent Lever Diagram of High Extended Range Mode
1.3 各工作模式差异性分析
对比式(1)和式(2)可知,CD1和CD2两种模式下的速度约束公式相同,车辆速度均受到MG1、MG2极限速度的制约,且车辆行驶的速度区间完全相同。由于CD2模式下双电机共同驱动车辆,耦合后的输出扭矩比CD1模式更宽,因此CD1适用于低速、低扭矩的工况,CD2模式适用于低速、大扭矩的工况。CS1模式下发动机的转速可通过MG1进行调节,MG1转速为负,工作于发电状态。车辆速度受到电机MG2极限速度的制约,转矩区间与CD2模式相同,CS1模式弥补了低速、大扭矩状况下纯电动驱动效率低下的不足,发动机启动于CD1向CD2模式切换的过程中,CS1适用于低速、大扭矩的工况。CS2模式下车辆的速度区间与CS1完全相同,高速行驶时,CS2模式发动机的转速相对较低,CS2与CS1两种模式下的转矩区间完全相同,中高速低扭工况下,CS2模式可使MG2工作于发电状态,从而拉高发动机的扭矩,使得发动机处于高效工作状态,CS2模式适用于中高速、低扭矩工况。相比于CS2模式,CS3模式的车速范围更宽,发动机转速与车速解耦,可直接通过调节MG1的转速使得发动机运转在高效工作区间。虽然与CS2模式输出转矩的工作区间完全相同,但CS3模式下MG2长期工作于发电状态,从而拉高发动机的扭矩,使得发动机处于高效工作状态,适用于高速低扭矩工况。

表2 不同工作模式对应的最优工况
1.4 高速增程模式系统传动效率分析
由前面的分析可知,高速增程模式下,行星排对发动机的机械功率进行多次分流,同时在输出端对所有分流后的功率再次进行汇流,为典型的复合功率分流模式,系统比较复杂。而机械能在转化为电能的同时存在能量转化的损失,随后电能再次转化为机械能,又存在能量损失,因此,机械能转化为电能越多,二次转化所造成的整体效率越低。对复合功率分流模式下的传动效率进行研究,能够确定机械结构的合理性。
1.4.1 传动机构动力学关系分析
图8所示为高速增程模式下各动力源以及变速箱的转矩传递关系。其中,TMG1、TMG2、TEng分别表示电机MG1、MG2和发动机的输出扭矩;TS1、TC1、TR1分别表示行星齿轮机构PG1作用在太阳轮、行星架和齿圈上的扭矩;TS2、TC2、TR2分别表示行星齿轮机构PG2作用在太阳轮、行星架和齿圈上的扭矩;TOut为地面对车轮端的扭矩经过主减速器后,作用在变速箱上面的倒拖扭矩;k1、k2分别表示行星齿轮机构PG1、PG2的特征参数。
忽略行星齿轮转动惯量以及各个齿轮之间摩擦力相互作用的影响,该模式下各传动机构动力学关系式可表示如下:

图8 复合功率分流模式下的转矩传递关系
Fig.8 Torque Transfer Relationship in Compound Power Split Mode

(6)
式中,IS1、IC1、IR1分别表示行星齿轮机构PG1太阳轮、行星架以及齿圈的转动惯量;IS2、IC2、IR2分别表示行星齿轮机构PG2太阳轮、行星架以及齿圈的转动惯量;K为主减速器传动比。
1.4.2 传动效率分析
在功率分流结构中,发动机功率可以通过机械路径和电路径两种方式传递到车轮,考虑到电路径存在二次转化使得整体效率降低,因此希望发动机功率通过电路径的部分越小越好。当发动机功率全部通过机械路径传递到车轮时,整车效率最高,电池的电功率为零[7][8]。在复合分流机构中,存在两种情况满足以上条件:1)电机MG1的转速为零,电机MG2的转矩为零;2)电机MG1的转矩为零,电机MG2的转速为零。将以上两种情况下的输出轴转速ωOut与发动机转速ωEng之比定义为机械点[8],即当传动比等于机械点时,电功率为零,发动机功率全部通过机械路径传递到车轮。
忽略各运动部件的角加速度,并假设电池的电功率为零,则公式(6)可以简化为:

(7)
推导得出电功率分流比如下:
(8)
式中,Pelect表示电功率,PEngine表示发动机功率,i1对应电机MG1转速为零时的机械点,i2对应电机MG2转速为零时的机械点,传动比i=ωout/ωEng。

图9 电功率分配比例曲线Fig.9 Distribution Ratio Curve of Electric Power
分析图8可知,当传动比i较小时,电功率分流比大于1,电机MG1的输出功率大于发动机输出功率,ηP_elect较大,且随着传动比的减小急剧增大。当传动比i等于i1时,ηP_elect为零。传动比i处于i1和i2之间时,ηP_elect较小,且最大不超过0.3。传动比i大于i2时,ηP_elect逐渐增大。因此,在变速箱机械结构的设计之初,应尽量使得变速箱的传动比处在两个机械点之间,传动比范围保持在0.4~1.5之间。
2 能量管理控制策略研究
2.1 能量管理策略控制架构
驾驶员模型根据车辆期望速度和实际速度反馈确定加速踏板或者制动踏板的行程,同时也确定了驾驶员的需求扭矩。能量管理模块根据驾驶员需求扭矩、电池实际SOC、车速以及各动力源的实时状态等信息进行工作模式的判断,同时根据离合器的开闭信号对各动力源进行扭矩分配。控制系统的整体架构如图10所示。
下文策略分析中所提到的符号以及其代表的含义见表3。
2.2 驾驶员需求扭矩
为了对不同工作模式下各动力源的输出扭矩进行分配,需要计算驾驶员需求扭矩[13]。本策略中根据车辆纵向动力学理论[9]计算车轮端的需求扭矩,同时根据整车期望速度与实际速度的差值,采用PI控制器计算补偿扭矩。
Twheel=Fwheelrw
(9)

图10 能量管理控制系统架构Fig.10 Structure of Energy Management Control

表3 逻辑门限控制参数定义
Fwheel=FR+FG+FD+Fa
(10)
(11)
式中,Fwheel为车轮端的驱动力,FR、FG、FD、Fa分别代表车轮滚动阻力、坡度阻力、空气阻力和加速阻力。rw为车轮滚动半径,ig为主减速器减速比,ΔT为由PI控制器计算的补偿扭矩。
2.3 工作模式切换控制
1.3节分析了不同工作模式所对应的最佳行驶工况,基于此进行工作模式切换控制逻辑的开发。
2.3.1 纯电动模式
当v≤Vev_max且SOCrel≥SOCCD_min时,为纯电动模式。
(1) 若整车需求扭矩0≤TDem≤TMG2_high时,进入纯电动模式1(CD1模式);
(2) 当TMG2_high≤TDem≤TMG2_high+TMG1_high时,进入纯电动模式2(CD2模式);
(3) 当v≥Vev_max或SOCrel≤SOCCD_min时,退出纯电动模式,随后控制电机MG1拖动发动机启动,进入增程模式。

图11 驾驶员需求扭矩计算框图Fig.11 Block Diagram for Calculating Driver Demand Torque
2.3.2 增程模式
发动机启动后即进入增程模式。
(1) 当整车车速较低、功率需求较大时,为了兼顾发动机的运行效率,需要保证发动机转速n≥ne_min,此时应该选择低速增程模式,通过控制电机MG1反转拉高发动机转速。MG1处于发电状态,获得的电量提供给电机MG2。
(2) 当电池电量SOC≤SOCCS_min时,需要对电池进行充电,基于减小系统损失考虑,选择固定速比增程模式,此时锁定电机MG1,通过控制MG2作为发电机为电池充电。
(3) 当整车车速需求较高时,选择高速增程模式。
2.4 发动机控制
增程模式下,对于发动机的控制需要始终围绕发动机的外特性曲线以及燃油消耗特性曲线来展开。确保在提供充足动力的同时使得发动机的燃油消耗量尽可能低。图12所示为发动机外特性曲线,通过等功率曲线与燃油消耗特性曲线的交点拟合得到发动机的最优工作曲线。对于发动机的控制策略需要保证发动机的工作点始终处于最优工作曲线上。

图12 发动机特性曲线Fig.12 Engine Characteristic Curve
2.4.1 发动机转速控制策略
由前述分析可知,增程模式除了CS2模式下电机MG1锁止以外,其他两种模式发动机和MG1均通过行星排1实现转速耦合,发动机转速与车速解耦,因此当控制器实时分配给发动机某一转矩值时,发动机在相应的等功率线上运行,可通过调节电机MG1的转速来调节发动机转速,从而使得发动机的工作点处于最佳效率点。但是当需求功率较低时,即使发动机的工作点在最优曲线上,此时的燃油消耗率还是很高,因此有必要划分发动机的高效区域从而对发动机设定转速限制,ne_min为发动机高效区域转速下限值,ne_max为发动机的上限值,根据发动机的转速限制将整车车速划分为低,中,高三个区域[10]。当车速低于VL时,如前所述的转速耦合关系能够避免发动机转速过低。由于发动机的转速只与电机MG1耦合,与电机MG2无关,因此只需要通过分析单行星排PG1即可确定车速VL和VH的值,如下图14所示,定义转速向左方向为负,向右方向为正。车速VL的确定取决于发动机的转速ne_min,此时电机MG1的转速为0,车速VL可表示为:

图13 发动机输出转矩特性Fig.13 Engine Output Torque
(12)
车速VH的确定取决于发动机最大转速ne_max,同样电机MG1的转速为0,VH可以表示为:
(13)
式(12)和(13)中,k1为行星排PG1的特性参数,rw为轮胎半径。
(1) 当车速V≤VL时,控制电动机MG1反方向运转从而保证发动机维持在在最小转速ωEng_min,MG1转速可表达为:
(14)
电机MG1作用在太阳轮S1上的转矩方向与电机的旋转方向相反,处于发电状态,忽略电机的功率损失,可以计算得到电机MG1的功率:
(15)
(2) 当车速VL≤V≤VH时,锁定电机MG1,此时发动机与电动机MG2以转矩耦合模式运行,发动机转速正比于车速。中转速区间内,忽略发动机的机械损失,所有发动机功率全部传递到输出轴。
(3) 当车速V≥VH时,为了保证发动机维持在最大转速ωEng_max,需要控制电机MG1沿正方向转动,此时MG1作为电动机,计算其电驱动功率为:
(16)
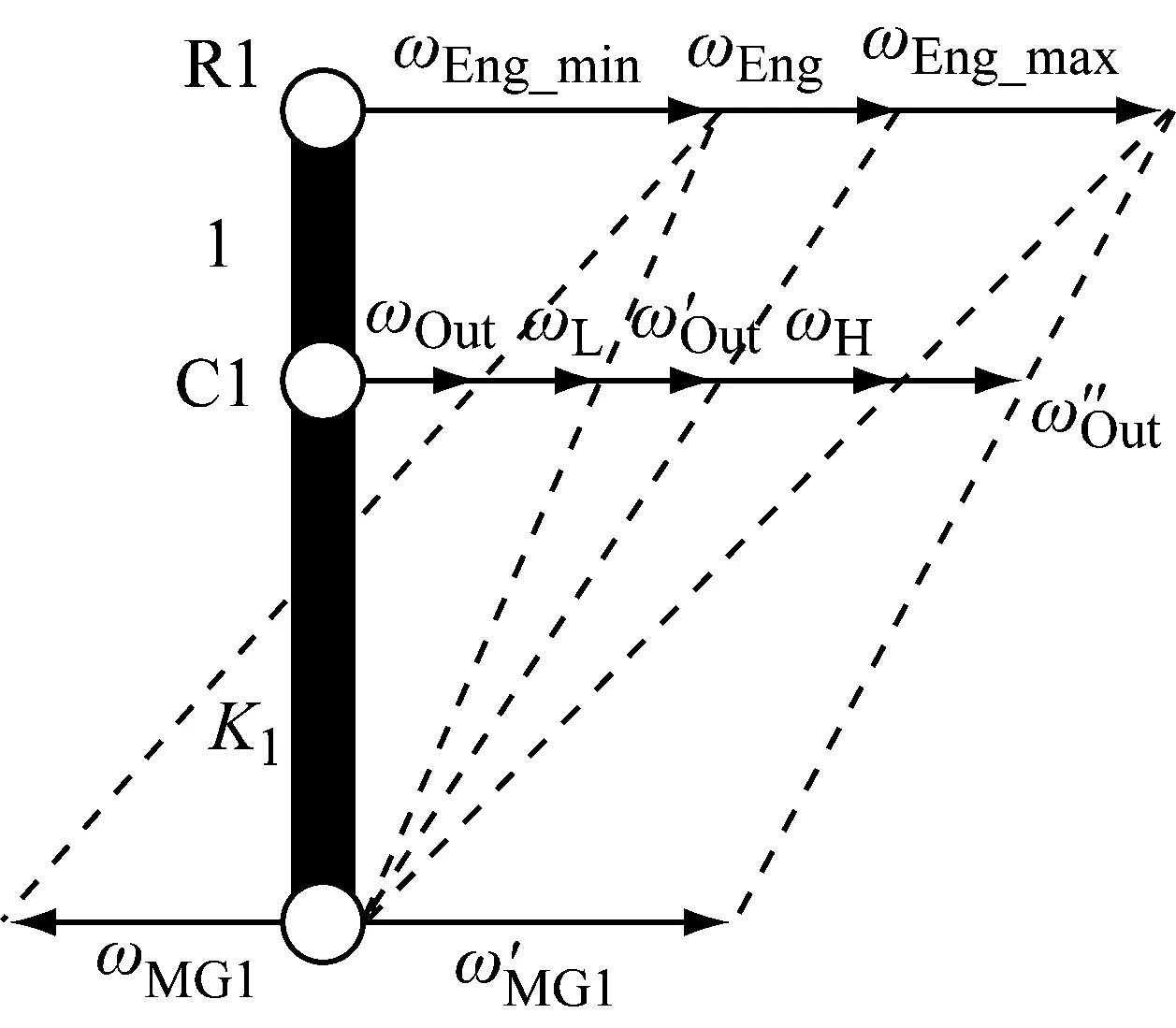
图14 发动机转速等效杠杆图Fig.14 Equivalent Lever Diagram of Engine Speed
2.4.2 发动机转矩控制策略
发动机的转矩控制建立在前面转速控制的基础之上。增程模式下,发动机的转矩与电机MG2的转矩相耦合,当整车的需求扭矩一定时,且发动机转速确定后,通过调节MG2的转矩使得发动机转矩尽量靠近最优曲线,以实现减小油耗的目的。
(1) 当车速处于低车速区域内,即V≤VL,发动机以最小速度ne_min运转。
若此时整车的需求扭矩大于发动机在该转速下所对应的最优转矩时,如图15所示A点,应该尽量调整电机MG2的转矩使得发动机运行在图中B点,即发动机提供功率TB,电机MG2提供功率TA-B。但是电机MG2由于电池电量的限制,并不能在所有状况下都能够提供所需的转矩TA-B。当电池实际电量SOCrel≥SOCCS_min时,能够给电机提供充足的电量,则电机MG2提供转矩TA-B;但当电池电量SOCrel≤SOCCS_min时,基于电池的寿命考虑,不宜输出功率,电池处于静默状态,则电机MG2唯一的功率来源于MG1的发电功率见式(15),计算出此时MG2的输出扭矩为:
(17)
为了满足车辆的动力性需求,控制器适当提高发动机的扭矩请求TB′≥TB,使得TB′=TDem-TMG2。
若整车的需求扭矩小于发动机在该转速下所对应的最优转矩时,如图15所示C点,根据电源的SOC状态又存在多种情况当SOCrel≤SOCCS_min时,发动机运行于点B,提供最优输出扭矩TB,电机MG1发电,功率如式(15),电机MG2提供扭矩-TA-B,即电机MG2也作为发电机为电池充电。当SOCCS_min≤SOCrel≤SOCCS_max时,电机MG2的功率全部由发电机MG1提供,即TMG2,发动机的实际输出扭矩TB′≤TB,TB′=TDem-TMG2。当SOCrel≥SOCCS_max时,此时关闭发动机即进入CD2模式。

图15 发动机转矩控制策略示意图Fig.15 Scheme of Engine Torque Control Strategy
(2) 当车速处于中速区域内行驶时,即VL≤V≤VH时,关闭电机MG1,发动机和电机MG2为转矩耦合,发动机的速度正比于车速。
(3) 当车速处于高速区域内行驶,即V≥VH时,发动机以最大转速ne_max运转。电机MG1的转速方向与转矩方向相同,作为电动机从电池吸收能量驱动车辆。
当车辆的需求扭矩大于发动机在该速度下对应的最佳扭矩时,如图15所示G点,且当电池的荷电状态SOCrel≤SOCCS_min时,电池不宜进行放电,通过分析该双模机构的构型发现,在车辆行驶状态下,电机MG2也必须处于运转状态,否则,由于车辆的惯性远大于电机MG2的惯性,从行星排PG1传来的动力不能有效地传递到车轮,仅仅使得MG2空转。在这种情况下仅存在一种解决方法,即通过控制发动机的转速大于当前车速V所对应的固定速比模式(CS2)下发动机的转速,迫使电机MG1反转,MG1作为发电机运行后产生的电能提供给电机MG2,电池不参与能量的流动。这种方法使得发动机的转速远高于其最大转速限制,油耗增大,且不一定能够满足整车的扭矩需求。一般应该尽力避免在电量不足的情况下进行高速行驶。当电池的荷电状态SOCrel≥SOCCS_min时,发动机以最大转速ne_max运转,此时由发动机和电机MG2共同牵引车辆行驶。
当车辆的需求扭矩小于发动机在最大转速下对应的最佳扭矩时,如图15中K点,且当电池荷电状态SOCrel≤SOCCS_max则控制发动机运行在H点,即发动机提供扭矩TH,电机MG2作为发电机提供负向扭矩-TH_G。当SOCrel>SOCCS_max时,发动机停转,切换至纯电动模式。
2.5 电机控制
在确定了发动机的最优转矩和转速之后,电机MG1的准静态扭矩可根据公式(3)计算得到:
(18)
电机MG2的准静态扭矩可根据整车需求转矩和发动机需求转矩计算得到:
(19)
由于发动机的转速需要通过电机MG1调节,因此电机MG1的扭矩还需要根据发动机期望转速与实际转速之间的差值,由PI控制器进行补偿,具体的控制框图见下图(16)。

图16 电机MG1需求扭矩计算框图Fig.16 Block Diagram for Calculating Demand Torque of MG1
3 仿真分析
为了验证能量管理策略的燃油经济性,将车辆模型置于新欧洲行驶工况(NEDC)(图17)下进行仿真。控制策略中各参数阈值的设定见表4,车辆参数以及相关动力总成参数见表5,建立的Simulink/Amesim联合仿真模型见图18。
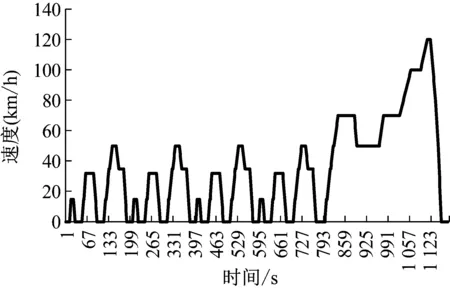
图17 NEDC行驶工况Fig.17 NEDC Driving Cycle
图19所示为NEDC工况下各动力源的转矩和转速。由图(a)可以看出在NEDC工况后期,较大的整车需求转矩使得发动机的介入时间较长。图(b)显示发动机启动后转速一直维持在700~4000 rpm区间内。图(c)和图(d)对比可见,大部分时间电机MG1的转矩和转速方向相反,即电机MG1处于发电状态,约1050 s以后,电机MG1处于驱动状态为车辆提供额外的转矩需求。通过图(e)和图(f)可以看出,电机MG2的转速与整车转速相反且呈比例关系,且当整车减速时,电机MG2的转速和转矩方向相反,处于发电状态回收制动能量。
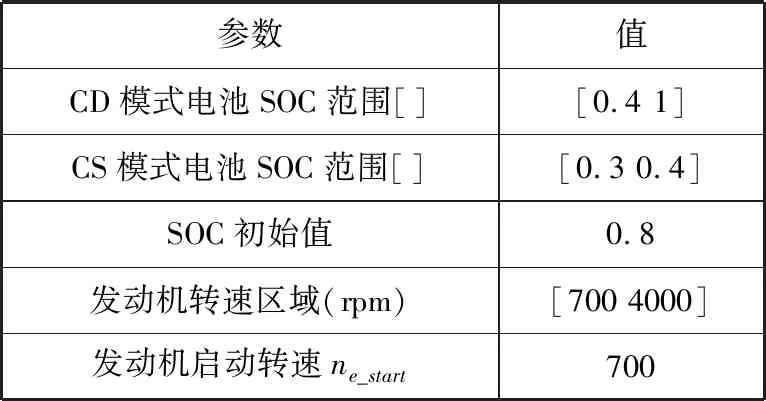
表4 控制器中定义的阈值

表5 整车基本参数
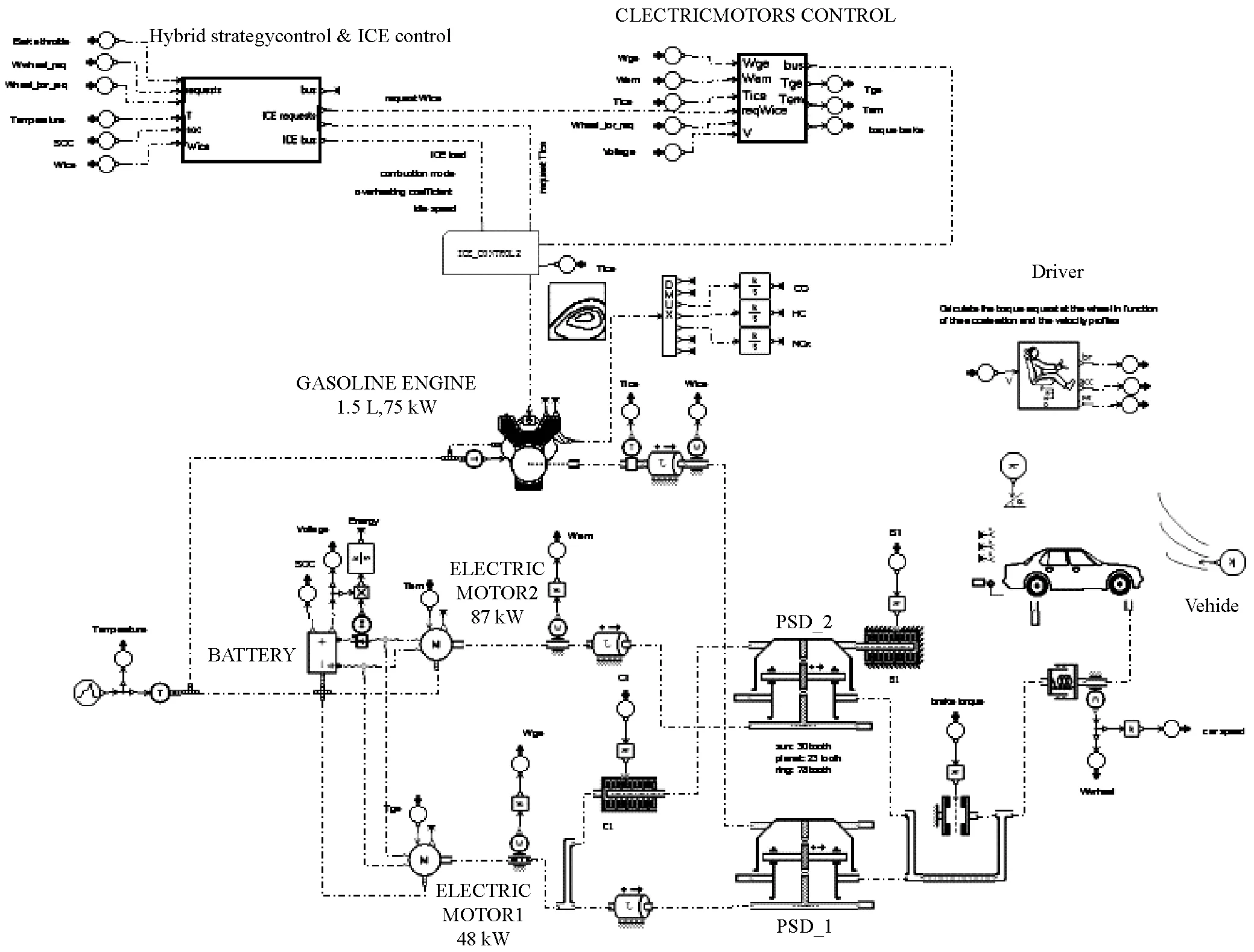
图18 Simulink/Amesim联合仿真模型Fig.18 Simulink/Amesim Co-simulation Model
为了直观的判断策略的有效性,图20给出了发动机不同转速下的实际输出转矩,可以看出发动机的实际转矩大多数情况下都能够很好的集中在最优曲线附近。图21所示为NEDC工况下电池SOC的变化,其初始SOC为0.8,当电量下降到0.6附近时即对电池充电,使得电池的SOC维持在预定的范围之内。

(a) 发动机转矩

(b) 发动机转速

(c) 电机MG1转矩
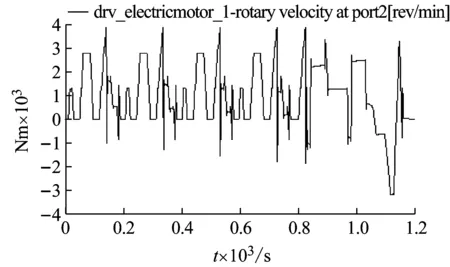
(d) 电机MG1转速
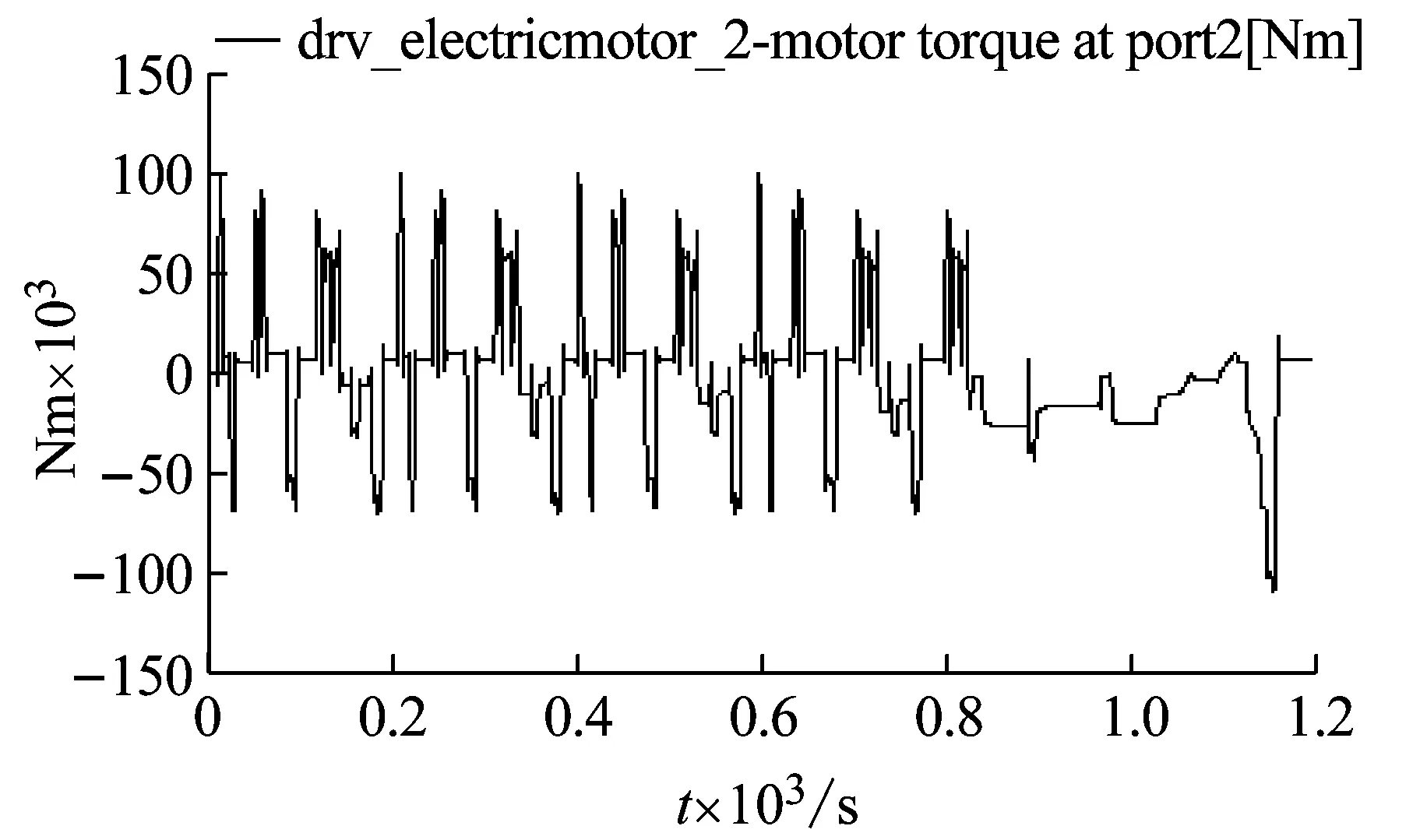
(e) 电机MG2转矩

(f) 电机MG2转速
图19 NEDC工况下各动力源转矩和转速
Fig.19 Torques and Speeds of Power Elements in NEDC Driving Cycle

图20 不同转速下发动机实际输出扭矩Fig.20 The actual Output Torque of the Engine at different Speeds

图21 NEDC工况下电池SOCFig.21 Battery SOC in NEDC Driving Cycle
4 总结
(1) 针对一款功率分流式行星齿轮机构,分析了不同运行模式下发动机、电机MG1、电机MG2以及整车之间的转速转矩耦合关系,同时对高速增程模式下系统的传动效率进行了分析,在此基础上制定了模式切换逻辑。
(2) 制定了以发动机为控制对象的能量管理策略,根据混合驱动模式下发动机与整车转速转矩解耦的特点,通过分别控制电机MG1和电机MG2使得发动机运行在最优工作曲线上。
(3) 建立了Simulink/AMESim联合仿真模型,将模型置于NEDC工况下进行仿真,仿真结果表明,不同转速下发动机的实际输出扭矩始终在最优曲线附近波动,同时电池的SOC维持在合理的范围内,验证了策略的有效性。
