由两端弹性支承的对称梁导出对称简支梁的多项式型位移函数

何 敏，江燕燕，黄 忠，周清卿，王其申

（安庆师范大学物理与电气工程学院，安徽安庆246133）

2001年，Elishakoff等针对功能梯度梁的横向振动问题，提出了一种新颖的解法[1-2]。此后，王其申研究了任意支承杆模型[3]，吴磊等研究了简支梁[4]和悬臂梁[5]这两类单跨梁，王其申等进行了相关问题综述[6]。对于多跨梁结构，文[7]研究了一类两跨梁模型，文[8]研究了两跨外伸梁模型，文[9]研究了对称简支梁模型。本文由两端弹性支承的对称梁出发，最终导出对称简支梁的多项式型位移函数。

长为L的梁的横振动无量纲动力学方程：

对于两端弹性支承对称梁，参考文[10]，有下列边界条件：

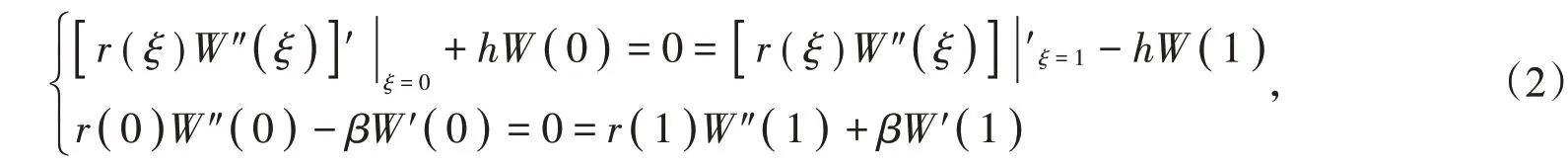
其中，h是约束梁两端线位移的拉伸弹簧刚度，β是约束梁两端角位移的扭转弹簧刚度。

下面计算两端弹性对称梁的多项式型位移函数。要满足条件（2）式，对于基模态（也称第一阶模态或不含节点的对称模态），可以把位移多项式取为4次多项式；对于第二阶模态（也称含单节点的反对称模态），可以把位移多项式取为5次多项式，还要满足约束条件W()=0。令

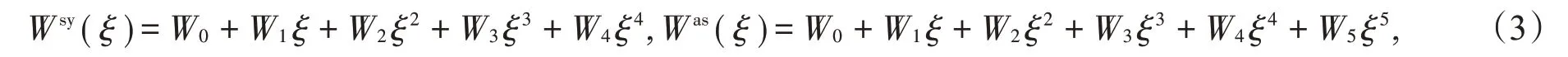
这里，上标sy表示对称振型，上标as表示反对称振型。解得满足边界条件的位移多项式是：

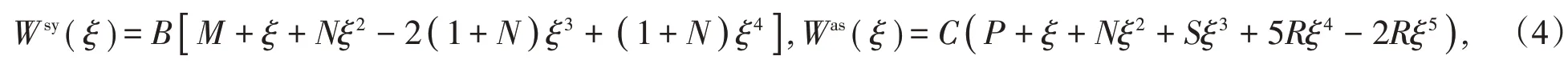
经过化简，（4）式可以化为如下的多项式型函数：

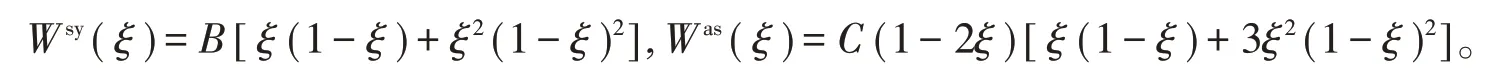
此结论与文[9]完全一致。而对于两端固定的对称梁，需要满足极限条件h →+∞, β →+∞，则（4）式中的系数N →+∞，这是不能成立的。因此，可以由对称多项式型函数（5）式导出对称简支梁的多项式型位移函数，但不能导出两端固定对称梁的多项式型位移函数，这反映了这个模型具有局限性。

本文计算结果表明：由两端弹性支承的对称边界条件，可以构造两端弹性支承对称梁的多项式型位移函数，它包含了对称简支梁的位移函数。文章计算的基模态和第二阶模态下两端弹性支承梁的多项式型位移函数，在相差一个常数因子的条件下，位移函数是唯一的。