基于编解码双路卷积神经网络的视觉自定位方法
2019-11-21贾瑞明刘圣杰李锦涛王赟豪潘海侠
贾瑞明,刘圣杰,李锦涛,王赟豪,潘海侠
(1.北方工业大学 信息学院,北京100144; 2.北京航空航天大学 软件学院,北京100083)
视觉自定位(Visual Localization,VL)是一种通过待查询的视觉数据来获取相机位姿的方法,其在计算机视觉中扮演着重要的角色,在航天器交会对接、轨道飞行器回收空间碎片、火星漫游车等应用场景中,均需要通过视觉自定位技术获取精确的自身位姿参数。不同于从运动恢复结构(Structurefrom Motion,SFM)及即时定位与地图构建(Simultaneous Localizationand Mapping,SLAM)提供图像序列间的相对位置关系,视觉自定位直接给出待查询的视觉数据对应的相机绝对位姿。视觉自定位可以分为直接法和间接法。间接法通常的做法是将待查询图像与一系列相似的候选图像比较以获得位置,这成为一种图像检索问题[1-3]。直接法从待查询图像中直接恢复相机位姿,大致可以分为如下3种方法:①假设已知待查询图像对应的相机位姿的先验知识,可以得到一个粗糙的位姿预估计。先验知识可以从定位传感器(如GPS[1,4-5])中获得。②利用特征点匹配[6-9]来实现,通过计算从二维待查询图像中提取到的特征在三维点云模型中的对应来获得相机位姿。这通常需要使用从SFM 或其他方法中重建的三维模型。③直接从输入视觉数据中估计出对应的位姿信息,有标准预测技术[10]和利用卷积神经网络(Convolutional Neural Network,CNN)的方法。
随着深度学习的发展,神经网络在实现室内或者室外场景的坐标定位问题上体现出很好的精度。相比于传统算法,深度学习方法在处理有复杂纹理的场景、不同光照的环境、有运动模糊等挑战性因素的数据集时具有良好的鲁棒性。本文讨论的算法属于直接法视觉自定位中的第3种方法,即运用卷积神经网络直接从待查询视觉数据中估计出对应相机位姿。
2015年,Kendall等[11]提出的网络PoseNet尝试直接从输入图像恢复六自由度的相机位姿,作为使用深度学习处理视觉自定位问题的开拓性工作,使用了第1版GoogleNet作为PoseNet的基础网络,将该网络的3个softmax分类器替换为1个全连接层,之后输出位置坐标和姿态角四元数。2016年,Walch等[12]对PoseNet提取到的特征进行调整,将这些特征不直接输出到预测器,而是作为空域LSTM的输入序列,得到了更精确的结果。科研人员还研究了如下代表性方法:Clark等[13]在时域上运用了LSTM 结构,利用视频帧间的时域信息来辅助预测相机位置,但仅有相机位置信息而缺少姿态信息;Kendall和Cipolla[14]提出了运用模型不确定性的贝叶斯PoseNet,在多个随机裁剪的输入图像和PoseNet之间插入了一个dropout层,并为每个生成的位置建模,提升了定位精度;Melekhov等[15]提出了一种沙漏网络结构,使用ResNet34网络结构代替PoseNet的GoogleNet,并使用反卷积及跳跃连接,定位精度超过了其他成果;Li等[16]提出利用深度图进行研究,相比PoseNet提升了精度,但引入了附加深度信息,由于真实场景中可能无法有效获取深度信息(如使用数码相机),不利于实时定位。其他方法如使用附加的语义信息及视觉里程计进行约束[17-18]、估计像素级坐标之后利用RANSAC进行匹配[19],虽然提升了算法精度,但是大幅增加了算法复杂度及需要提供的信息。
本文提出了一种编解码双路视觉自定位网络(Bifurcate Localization Net,BiLocNet)结构,可以从单张RGB图像预测相机六自由度位姿参数;该网络使用改进的Inception-Resnet-V2作编码器,用双路结构解码输出位置和姿态参数,提出一种多尺度位姿预测器结构,从解码后的特征图中预测出相机位姿;由于数据集较小,其他方法[11,13,15,18,20]均利用在ImageNet上进行预训练的模型权重来执行权重初始化,该网络无需预训练即可达到优于预训练模型的收敛速度和精度;此外,损失函数加入同方差不确定性[21]作为目标函数,提升了网络可训练性。
1 编解码双路视觉自定位网络结构
本文提出了一种编解码双路视觉自定位网络结构,如图1所示,其由编码器(encoder)、解码器(decoder)和 预 测 器(estimator)组 成。首 先,BiLocNet用编码器对输入图像进行编码以提取高级语义特征;然后,采用双路解码器、预测器分别解码输出位置p和姿态q。其中,在编、解码之间加入跳跃连接使编码部分的空间信息可以传递给解码器,对解码过程中的空间信息缺失进行一定程度的补偿。
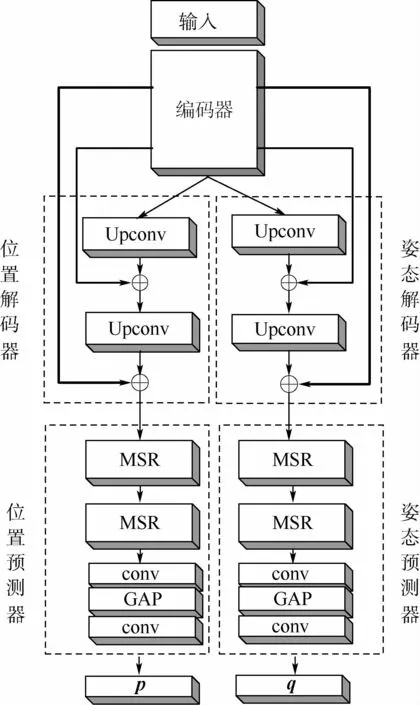
图1 BiLocNet结构Fig.1 Architecture of BiLocNet
1.1 编码器
编 码 器 由 改 进 的Inception-Resnet-V2[22]组成,Inception-Resnet-V2如图2所示。编码器中,stem结构用于维持基础网络层结构的稳定。Inception-Resnet有A、B、C共3种模块,区别在于卷积核的尺寸、通道数和子分支。Inception-Resnet模块使用最大值池化层及多尺度卷积层获得不同尺度下的特征,同时结合ResNet的思想,将残差模块中的残差结构替换为上述多尺度结构,既保留了Inception一贯的拓宽及加深网络的思想,又改善了过深的网络可能出现的梯度消失及梯度爆炸问题。残差模块还使网络梯度回传更加有效,从而显著提高网络收敛速度。Reduction模块用于降低分辨率、提升通道数,达到甚至超越传统卷积神经网络中利用最大值池化层接卷积层得到的效果。
由于本文网络在编、解码之间增加了跳跃连接,为了保证跳跃连接节点的特征图的分辨率相同,调整了池化层及部分卷积层的填充方式以适应解码器输出的特征图尺寸,从而使编码器中间层输出特征与解码器恢复的特征可直接相加,还调整了某些输出通道数以避免出现原网络某些层之间张量维度不匹配的情况,同时去除了图2中的dropout层、全连接层(FC)和softmax层,使输出的特征向量不经过分类任务的预测器而直接作为解码器的输入。
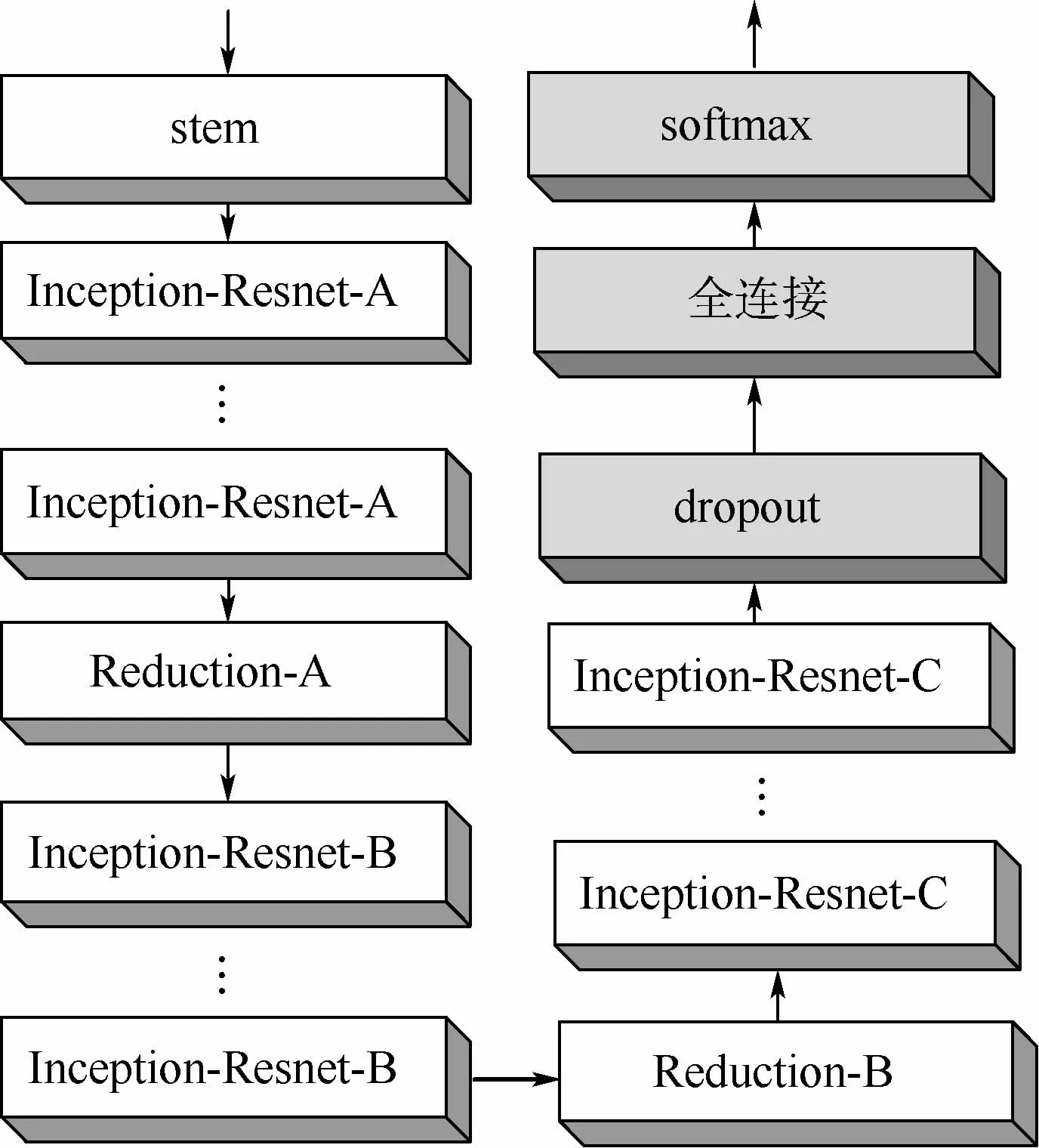
图2 Inception-Resnet-V2编码器结构Fig.2 Architecture of encoder Inception-Resnet-V2
1.2 解码器
由于编码过程中特征图的空间分辨率会逐步降低,导致了神经元间的空间信息被压缩,而这种空间依赖关系对于图像处理任务至关重要,故本文在编码之后加入解码器。
解码器采用2个上卷积层,卷积核大小为4×4,步长为2,每次上卷积之后特征图分辨率变为原来的2倍,通道数也相应降低。解码器尝试从高维特征中恢复特征间的空间信息,且增加了网络的深度,对预测精度有显著提升。同时,为了更好地保持编码过程中的图像细节信息,编解码之间增加了2个跳跃连接(解码器有2个上卷积)。引出编码器Inception-Resnet-A、Inception-Resnet-B后的2个特征图,与上卷积后的特征图分别相加,实现跳跃连接以弥补解码后恢复的空间信息损失。经过实验验证,增加解码器提升空间分辨率对于提升自定位精度有明显作用。
1.3 多尺度位姿预测器
预测器是深度学习回归任务中不可或缺的结构,解码后的特征图如要转换为需要的参数,需要使用预测器。
本文提出的多尺度位姿预测器结构如图1所示,主要分为多尺度降维(Multi-scale Reduction,MSR)模块和全局均值池化模块(Global Average Pooling,GAP)。如图3所示,MSR模块由1×1和3×3两种尺度的卷积层组成,一共包含5个卷积层,conv代表卷积层,k代表卷积核大小,s代表步长。解码出的信息经过第1个MSR模块,输出特征图大小将变为输入特征图的一半,将得到的输出经过第2个MSR模块,输出特征图分辨率再次减半。GAP模块包含一个用于降分辨率升通道的卷积层、一个全局均值池化层及一个1×1卷积层,最终输出一个特征矢量。
MSR模块用于将解码器输出的特征进行重组,使其通过不同尺度的卷积核获得不同的感受野,同时将这些特征进行降维升通道为接下来的预测做准备,且MSR模块拓展了网络的深度和宽度,有效提升了网络性能。单尺度降维模块(Single-Scale Reduction,SSR)结构如图4所示。
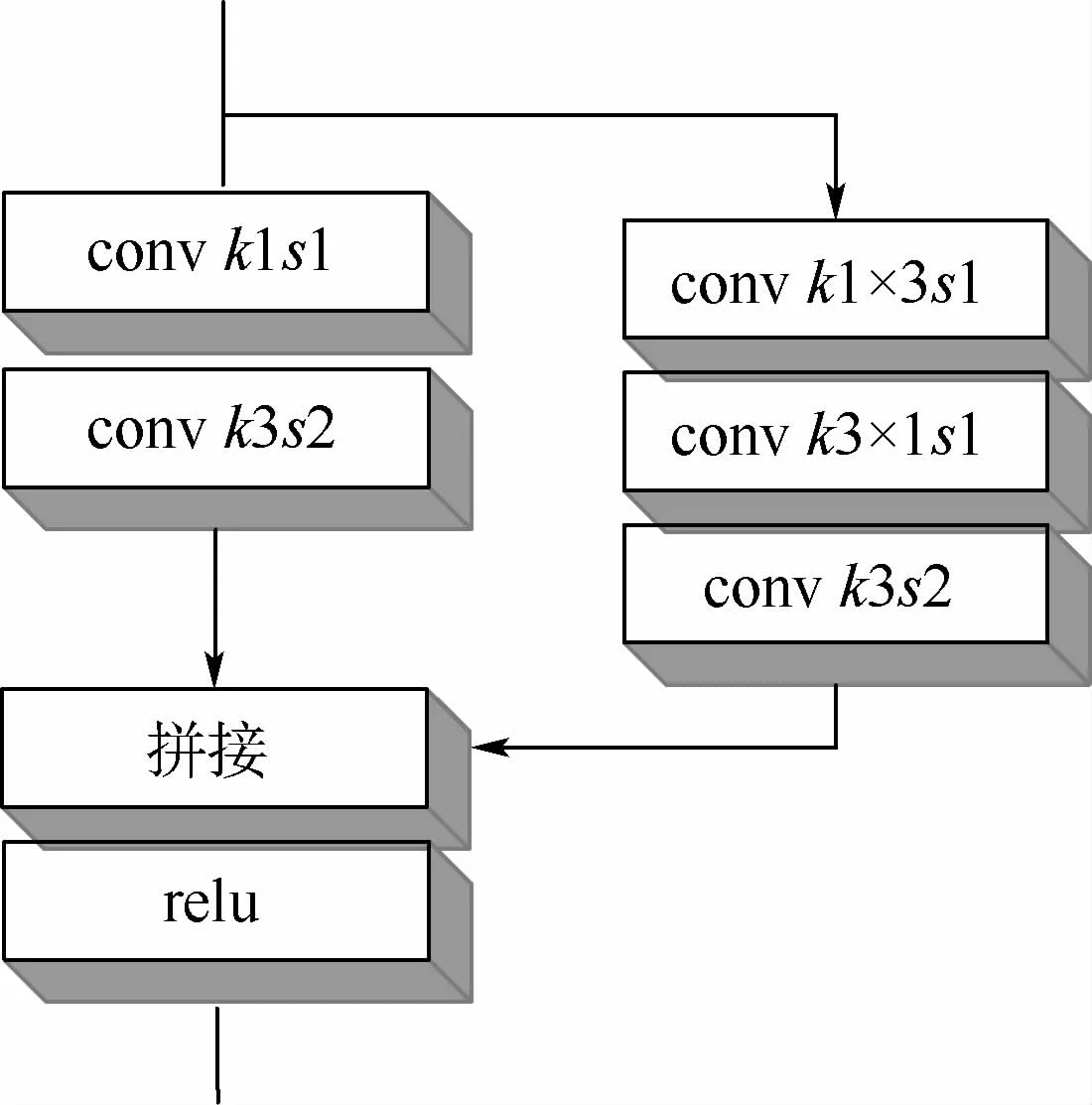
图3 MSR模块结构Fig.3 Module architecture of MSR

图4 SSR模块结构Fig.4 Module architecture of SSR
1.4 双路结构
目前,视觉自定位网络中位置与姿态参数均从单路网络输出,未考虑位置和姿态的区别,本文根据位置与姿态的不同特性,采用双路结构分别处理位置参数和姿态参数。
视觉自定位输出六自由度参数,包括3个位置和3个姿态角度。位置与姿态有以下不同:①相机的位置和姿态具有不同的量纲;②相机位置和姿态的改变反映在二维图像中是不同的,位置的变化将导致图像中物体间的遮挡关系及像素位置发生变化,而姿态的变化导致了视角的变化。真实世界在图像中的投影对于位置和姿态变化的表现是不同的,根据投影关系可知,视角变化会使物体在图像中的大小和形状发生变化。
综上可知,不分离位置和姿态而直接单路输出会导致两者间互相干扰,使网络无法精确解算位姿信息,故本文将位置和姿态考虑为2种任务,设计了双路网络来解决此问题。多任务学习通过从共享的特征表示中同时学习多个任务的特定表示,提高了学习效率及预测精度。多任务学习是一种任务之间的知识共享和迁移,从一个任务中学习得到的表示通常可以帮助改善其他任务。BiLocNet将编码器输出的特征矢量分裂为位置和姿态两路子任务网络。
2 损失函数
相机位姿中,位置p由相机在世界坐标系中的坐标[x,y,z]表示,姿态q由一个四元数q=[v,a,b,c]T表示。
四元数可以表示三维空间中任意一个旋转,避免了用欧拉角表示出现的万向锁现象。通过归一化为单位长度,任意的四维矢量可以很容易地映射到合理的旋转。使用四元数作为姿态角的优化目标比求取旋转矩阵要容易得多,避免了旋转矩阵增加的计算量及计算标准正交化矩阵。给定一个单位长度的旋转轴[i,j,k]和角度θ,对应的四元数为

给定一个欧拉角[φ,ρ,ω],[φ,ρ,ω]为沿着x-y-z坐标轴依次旋转的角度,将其转换为四元数的方法如下:
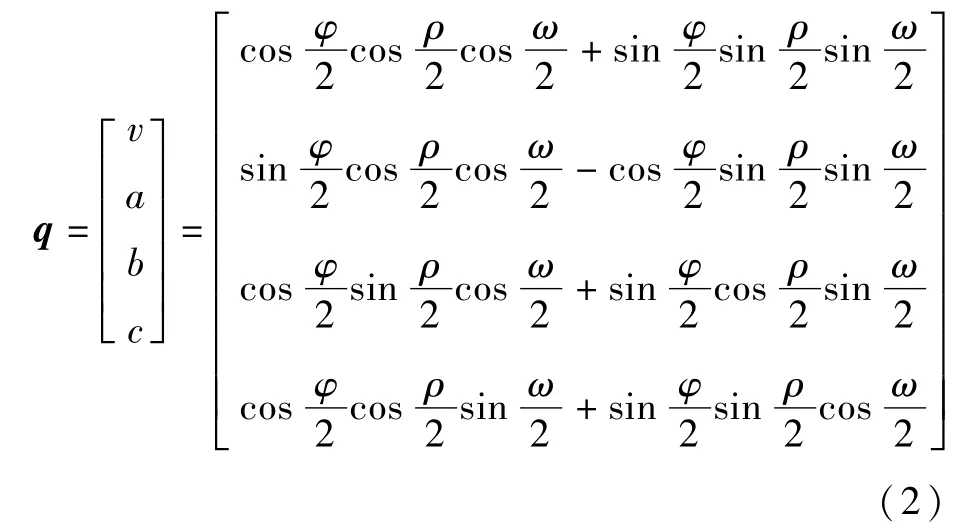
预测器分别输出一个维度为3的预测矢量^p和一个维度为4的预测四元数^q。预测误差如下:

式中:τ为距离范数。单位化的四元数存在于四维空间的球面上,当预测四元数^q足够接近q时,球面距离和欧氏距离的差异可以忽略[11],因此本文选择欧氏距离作为误差函数。在范数的选择上,由于L1范数对于所有样本点误差都以相同权重优化,而L2范数则给予不同的误差以不同的优化权重,且由于L1范数的一阶导数在极小值点附近也保持固定,损失函数值震荡较大。本文实验亦证明L2范数较优,故选用τ=2作为损失函数的范数。
单任务损失函数g定义为
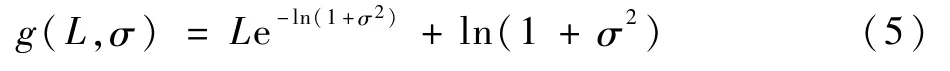
式中:L为式(3)或式(4)所示欧氏预测误差;σ作为模型的同方差不确定性[23]被加入损失函数中,设置为可训练参数。同方差不确定性是描述系统固有噪声的指标,如传感器噪声,特点是增大数据量也无法减小这种系统噪声。加入σ有助于增加网络可训练性。
为避免损失函数出现负值,未采用初始化σ2方法[21],而改为初始化σ,使正则项落在正实数区间,从而使网络收敛更加稳定。由于将位置和姿态看成2个任务,总损失函数定义为
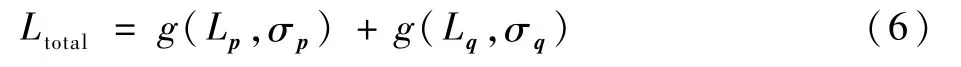
由于多任务之间的损失函数尺度大小不同,需要有不同权重来进行平衡以利于网络训练,所以本文的损失函数加入了不确定性。在训练过程中,网络自动学习平衡位置和姿态损失项的最佳权重σp、σq,既可以保证稳定优化Lp和Lq,同时作为正则项被加入损失函数又不会因为σ太大而使数据项权重太小导致网络无法收敛。
3 实 验
3.1 数据集
为便于与其他算法进行比较,使用Microsoft提供的7-scenes室内场景数据集[10]来评价本文BioLocNet结构。7-scenes数据集广泛运用于相机位姿估计任务,其包含7个场景,同时提供RGB及原始深度图。图像由KinectRGB-D传感器采集,真实位姿标注由KinectFusion[24]计算得出。每个场景的图像由分辨率为640×480的图片组成,被划分为训练集及测试集。场景具有复杂的纹理及光照信息,同时视角的改变和运动模糊也为相机位姿估计带来极大挑战。图5展示了7个场景的数据集图片,每个场景随机采样一张展示。
3.2 实验场景
按照官方推荐划分的训练集及测试集来训练和测试每个场景。本文使用 GPU 型号为NVIDIA1080 Ti,在内存为32GB、CPU为i7-6700的计算机上进行实验。程序在tensorflow框架下运行,初始学习率设为10-3,衰减率设为0.955,优化器使用Adam。在预处理阶段,每幅图像先缩放到343×343,随后减去每个场景图像均值再除以标准差,最后在线随机裁剪到300×300。在测试阶段,使用图像的中心裁剪进行测试。训练时,每个epoch将数据集顺序打乱。损失函数权重初始化为σp=0,σq=-1,batchsize设为16,迭代20×103~100×103步,训练网络直至收敛。
3.3 位姿估计精度
选用与其他算法相同的评价标准来评估本文的实验结果。通常的做法是分别求出测试集预测结果中位置和姿态的中位数进行比较。表1展示了本文结果与其他目前最先进算法结果的对比,所使用的网络为本文提出的BiLocNet。
表1给出了7个场景的测试误差,表中粗黑体数据表示该数据在横向对比中最优。实验结果表明,本文网络的表现超过了目前最先进的输入为RGB图像的同类型算法,有3个场景的位置精度达到了最优,6个场景的姿态精度超越其他算法,平均精度值也超越了其他算法。由实验结果可以看出,得益于将位置和姿态分别进行预测的双路网络,预测出的姿态精度大大超越了其他算法;且实验发现,只使用单路解码器及预测器的结构(Hourglass)在 Chess场景下位置误差为0.15 m,姿态误差为6.02°,比使用双路结构位置精度下降15%,姿态精度下降17%。实验结果证明了本文算法双路结构的必要性和有效性。

位置误差/m,姿态误差/(°场景)PoseNet[11] Bayesian DS[15] LSTM-Pose[13] Vid Loc[12] Hourglass[14]BiLocNet Chess 0.32,8.12 0.28,7.05 0.24,5.77 0.18,N/A 0.15,6.17 0.13,5.13 Fire 0.47,14.4 0.43,12.52 0.34,11.9 0.26,N/A 0.27,10.84 0.29,10.48 Heads 0.29,12.0 0.25,12.72 0.21,13.7 0.14,N/A 0.19,11.63 0.16,12.67 Office 0.48,7.68 0.30,8.92 0.30,8.08 0.26,N/A 0.21,8.48 0.25,6.82 Pupkin 0.47,8.42 0.36,7.53 0.33,7.00 0.36,N/A 0.25,8.12 0.25,5.23 Kitchen 0.59,8.64 0.45,9.80 0.37,8.83 0.32,N/A 0.27,10.15 0.26,6.95 Stairs 0.47,13.8 0.42,13.06 0.40,13.7 0.26,N/A 0.29,12.46 0.33,9.86均值 0.44,10.44 0.35,10.22 0.31,9.85 0.25,N/A 0.23,9.69 0.23,8.16
3.4 预测器结构分析
预测器的结构直接决定了解码后的特征如何映射为位姿矢量。
本文在网络解码部分尝试过全连接预测器,结构如图6所示,即将解码器的输出直接通过一个特征向量大小为2 048的全连接层做预测,发现其精度较差。这种情况的出现是因为全连接层将特征矩阵展开为一维特征向量,会损失特征矩阵的空间结构,更适用于分类任务,所以应避免预测器出现全连接层。本文进一步尝试使用GAP预测器,结构如图7所示,即将解码器输出使用卷积层降分辨率升通道,之后的全连接层替换为全局均值池化层,由于GAP避免了空间信息的损失及不必要的特征映射,并将解码器输出特征矩阵进行了调整,所以模型效果大幅提升。
为了比较不同预测器模型之间的差异,选择数据集中的一个Chess场景进行对比实验,结果见表2,其中多尺度位姿预测器指本文使用带有MSR模块的多尺度位姿预测器。
对于位置和姿态估计任务来说,使用MSR增加了网络的深度及宽度,其多尺度卷积核可以重组不同空间尺度的特征信息,保证了较高分辨率的特征图经过有效调整之后合理地映射为位姿矢量。经实验表明,将MSR(见图3)替换为SSR(见图4),精度下降8%,证明了MSR多尺度结构的有效性。
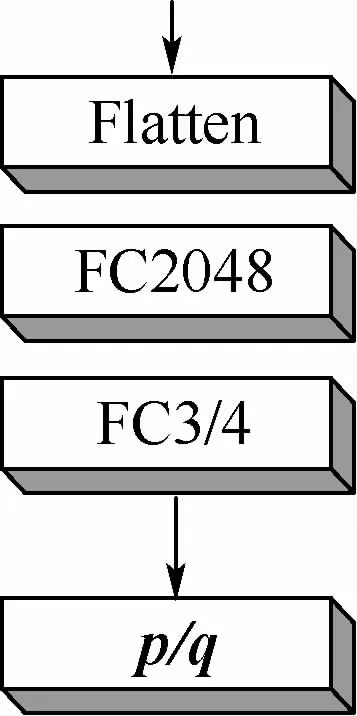
图6 全连接预测器Fig.6 FC estimator

预测器 位置误差/m 姿态误差/(°)全连接预测器0.26 8.03 GAP预测器 0.14 5.21多尺度位姿预测器0.13 5.13
3.5 损失函数分析
神经网络可以看为一个复杂的高维函数,而损失函数的选择是优化此高维函数至关重要的步骤。PoseNet的α权重损失函数定义为[11]

式中:α为平衡位置项与姿态项的权重。α权重损失函数的缺点是需要手动设置,欲达到最优效果,通常会使用网格搜索法来确定。在没有先验知识支持的条件下,耗时巨大且表现往往并非最佳。
本文引入了可训练的权重(σ权重)以自动地学习不同任务间的平衡(式(7)),效果优于α权重损失函数,在无MSR的BiLocNet上位置精度提升了10.5%,姿态精度提升了13.9%。数据见表3,同样使用Chess子数据集作为说明。
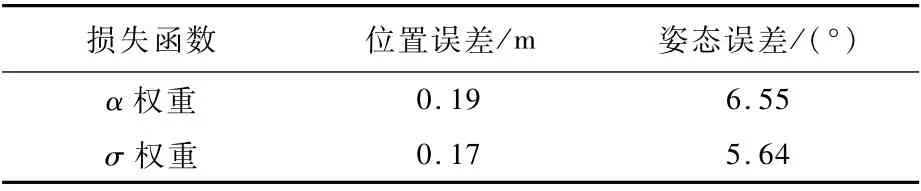
损失函数 位置误差/m 姿态误差/(°)0.19 6.55 σ权重α权重0.17 5.64
3.6 预训练分析
迁移学习指通过预训练从大数据集的分类任务中学习到特征的表示,将保存的权重模型加载到其他任务的网络作为初始化权重,从而加速网络收敛的一种方式。多数研究都借助于迁移学习的预训练模型初始化网络权重,但在本文网络结构下,无预训练的方式优于有预训练的方式,这是因为:①分类数据集与位姿估计数据集样本分布及内容相差较大,迁移学习得到的特征表示由于是从分类数据集中学得,用其作为初始化权重反而对位姿估计问题是有害的。②进行预训练需要花费较长的时间,使用数据集增强及增加迭代轮数等手段实现方便快速且在本文讨论问题上精度更优。何凯明等[25-26]也在研究成果中提到对于非分类任务,迁移学习可能并不会取得更好的效果。本文在数量为100 000的部分ImageNet数据集上进行编码器的预训练,并将训练好的权重作为网络训练前的权重初始化进行迁移学习。有无预训练的对比结果如图8所示。
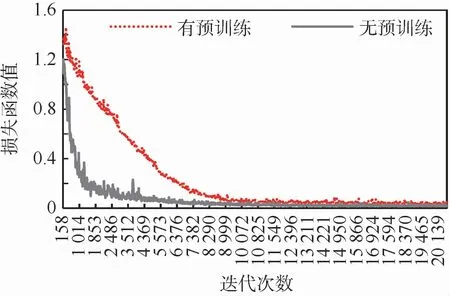
图8 有无预训练的BiLocNet损失函数曲线Fig.8 Loss function curves of pre-trained and non-pre-trained BiLocNet
可以看出,无预训练具有收敛速度快、收敛精度高的特点,可以快速使网络收敛到最小值附近。表4展示了有无迁移学习的结果对比。表中使用Fire场景作为测试场景,示例图片见图5。定性分析和定量分析结果均表明,在本文网络上使用预训练模型对结果没有提升,甚至有所下降。

有无迁移学习 位置误差/m 姿态误差/(°)0.32 10.64无有0.29 10.48
4 结 论
1)本文算法可实现较为优异的预测性能,在室内数据集上可将平均位置误差缩小至0.23 m,平均姿态误差缩小至8.16°。
2)跳跃连接和解码器可以补充编码过程中损失的空间信息,与多尺度位姿预测模块相互配合,可以大幅提升预测精度。
3)实验表明,由于数据集差异较大,迁移学习对于本文算法效果不佳。损失函数中加入可训练权重使网络的位姿精度平均提升了12.2%,且可以避免花费大量时间手动选择超参数。
4)研究待解决问题的特性有助于提升实验结果,本文算法挖掘位置和姿态的特性和区别,针对性地设计双路网络,使位姿精度平均提升了14%。
此外,依然有几个值得继续研究的问题:多任务之间通过训练得到的损失函数权重是否是最优解;解码器恢复特征图到什么程度的空间分辨率是最佳效果;2个子任务之间是否可以通过交互提升性能?下一步将继续研究这些问题。
