带限位隔振系统的冲击响应分析
2019-11-20刘海超冯麟涵
刘海超,闫 明,冯麟涵
(1.沈阳工业大学 机械工程学院,沈阳 110870;2.海军研究院,北京 100161)
舰船在作战中难免遭受水雷、鱼雷等敌方武器的攻击,由此产生的水下非接触爆炸冲击载荷虽然不会直接造成舰体结构的破坏,但会造成舰船设备的大面积失效,导致舰艇丧失战斗力和生命力[1-3]。目前,各国海军普遍采用在船体和设备之间添加隔振器的方法,既能降低设备的振动和噪声也能增强设备的抗冲击能力。隔振系统的固有频率一般都较低,因此在额定的冲击作用下,设备所承受的最大冲击加速度都不大,但设备相对船体的相对位移却较大,可能会超过设备与外界联接部件的允许值,甚至会超过了隔振元件本身的变形范围,因此,常在设备上安装限位器来降低设备的相对位移[4-6]。但是,一旦限位参数不匹配,极易造成更为剧烈的二次冲击问题[7-9]。为提高舰载设备的抗冲击性能,国内外学者进行了大量的研究。Pfeiffe等[10]采用拉格朗日乘子“将接触力预先乘入相应的雅可比矩阵”加在无接触的动力学方程上,并归为LCP问题以此来判断设备与限位器发生接触时的真实位形所在,此法需要花费较多的计算机时间。Feng等[11]提出了采用人工神经网络算法求解单边接触动力学问题并通过索结构的计算得到了很好的验证。温建明等[12-13]在Feng的基础上,利用高斯原理构造目标函数,求出神经网络状态方程,给出网络参数,通过神经网络算法对含有多个限位器的弹性浮筏系统的限位器接触状态进行决策,不仅使接触计算能够实现,同时大大降低了CPU 运行时间。但该计算方法复杂,存在一定的计算误差。Pogorilyi[14]借助Maple软件编写分段线性隔振系统的稳态时域响应和频域响应的计算程序,得出了冲击激励下分段线性对称系统频率响应近似解的求解方法,但对不对称分段线性系统响应的近似解没有找到有效的解决方案。楼京俊等[15-16]对新型气囊隔振系统进行了理论分析与试验研究,该型隔振系统能够起到一定的隔振缓冲作用,但是很难有效的限制相对位移,体积较大,气体存在缓慢泄漏等问题。赵应龙等[17-21]利用不同的有限元软件,对带限位隔振系统的冲击响应进行了仿真计算,探讨了限位器参数对系统抗冲击性能的影响,但为了简化模型都忽略或者弱化了限位器阻尼对系统抗冲击性能的影响,缺少相关试验验证仿真计算规律的合理性与准确性。
本文首先建立了包含隔振器刚度、阻尼,上、下限位器刚度、阻尼以及限位器安装间隙的八参数计算模型,各参数可独立设置,更适合研究限位器不同参数对带限位隔振系统抗冲击性能的影响。然后对该模型进行冲击仿真计算,分析限位器的刚度比和安装间隙对带限位隔振系统的抗冲击性能的影响。最后设计带限位隔振系统试验装置,在垂向冲击试验机进行了冲击试验,验证了仿真计算结果。
1 带限位隔振系统的构建
1.1 原理模型
带限位隔振系统原理模型如图1所示,M代表被隔振设备的质量;k1和c1分别代表隔振器的刚度和阻尼;k2和c2分别代表限位器的刚度和阻尼,Gap代表限位器的初始安装间隙。
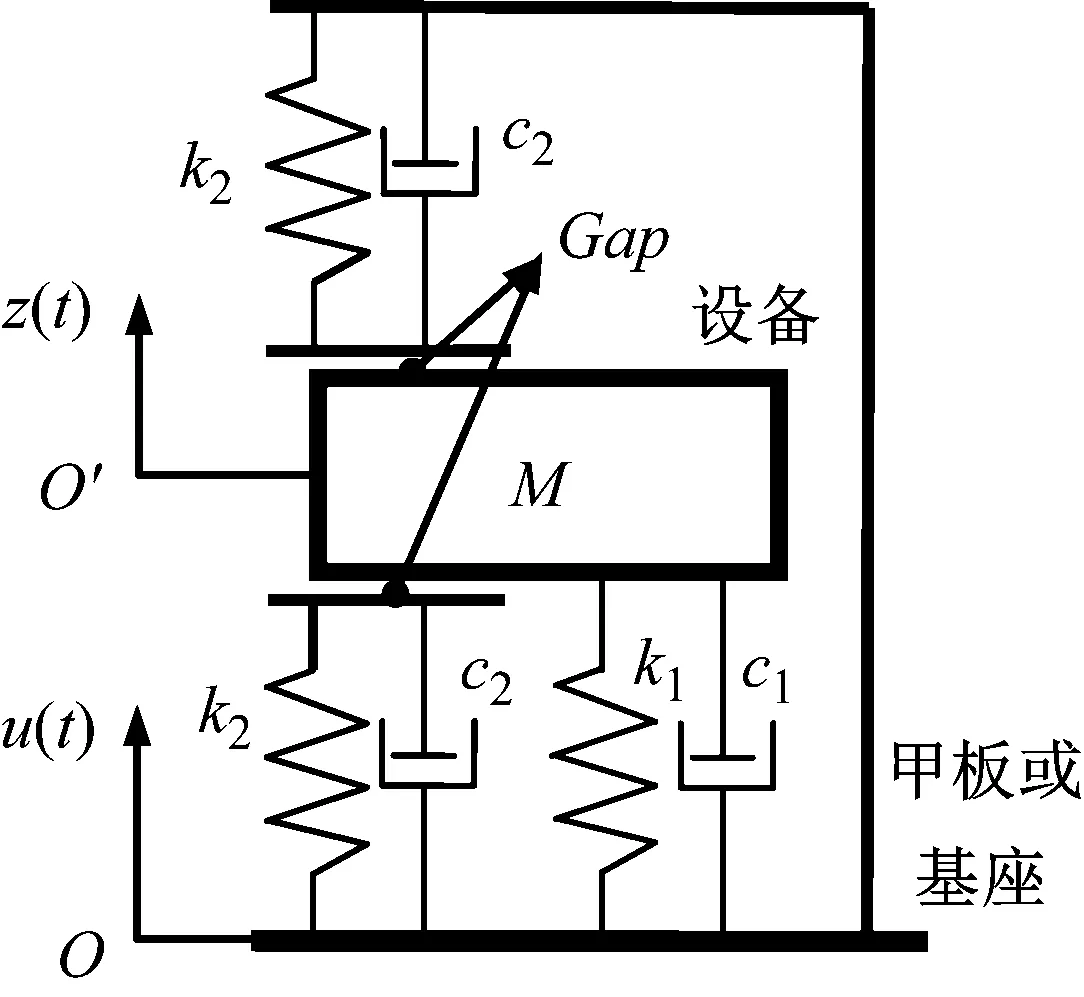
图1 带限位隔振抗冲击系统Fig.1 Limit vibration isolation system
1.2 数学模型
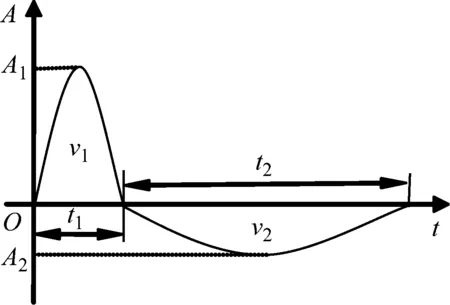
带限位隔振系统在冲击激励作用下,系统的响应分为两个阶段:即冲击载荷作用阶段,以及冲击载荷作用结束之后的残余响应阶段。在这两个不同的阶段,系统冲击激励不同,系统的等效刚度也不相同。通过分段线性的方法能够很好地解决这类问题,这里用x(t)=z(t)-u(t)表示设备的相对位移。在冲击激励的作用下,设备的相对位移和间隙主要存在以下三种关系
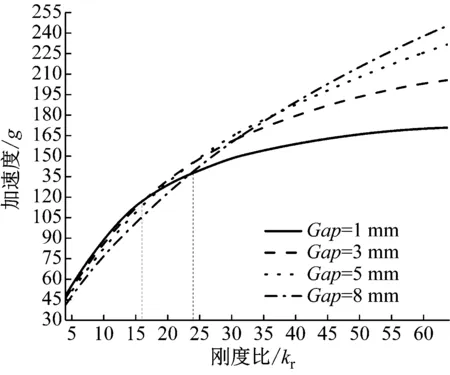
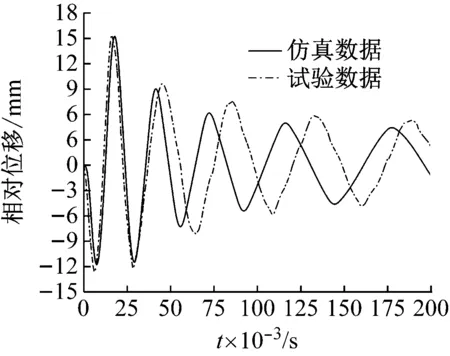
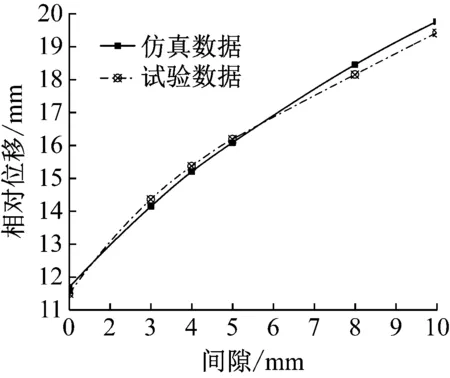
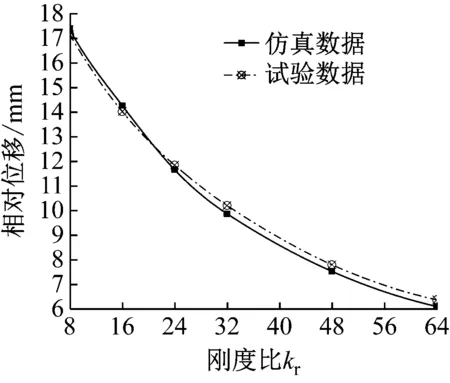
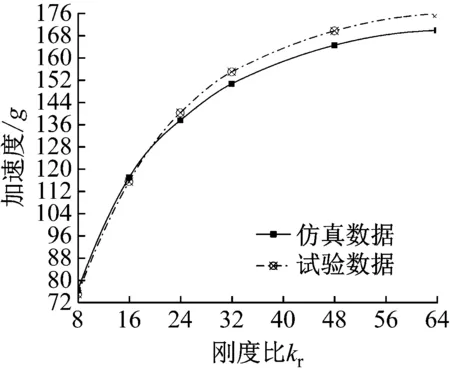
(1)当|x(t)| (2)当x(t)<-Gap时,由于设备的相对位移x(t)小于限位器的安装间隙-Gap,即与下限位器发生碰撞,所以隔振系统的刚度k等于隔振器的刚度k1与限位器刚度k2之和,同理隔振系统的阻尼c等于隔振器的阻尼c1与限位器阻尼c2之和。 (3)当x(t)≥Gap时,由于设备的相对位移x(t)大于限位器的安装间隙Gap,即与上限位器发生碰撞,所以隔振系统的刚度k等于隔振器的刚度k1与限位器刚度k2之和,同理隔振系统的阻尼c等于隔振器的阻尼c1与限位器阻尼c2之和。 根据以上的分析,当系统基础受到冲击激励时,根据牛顿第二定律可以得到设备的运动微分方程 (1) (2) 式中:A1是正波加速度幅值;A2是负波加速度幅值;f1与f2分别是正负波的频率;t1是正波加载结束时间,t2是负波加载结束时间。本文采用四阶龙格库塔方法求解上述微分方程。 根据德国军标BV043-85的相关规定,用图2所示的正负双半正弦波表示水下非接触爆炸冲击载荷,图中横坐标为时间,纵坐标为加速度,v1、v2分别代表正、负波速度,A1、A2分别代表正、负波加速度峰值,t1、t2分别代表正、负波冲击时间。 参照图2取A1=110g;A2=44g;t1=5 ms;t2=12.5 ms;v1=v2=3.5 m/s。 选取被隔振设备的质量为8 kg,隔振器的刚度k1为40 N/mm,阻尼比为0.005。记限位器与隔振器的刚度比kr如式(3),限位器的阻尼比ζc2如式(4),对带限位隔振系统施加上述正负双半正弦波的冲击载荷,分析限位器的安装间隙与刚度比对系统冲击响应的影响 2.1 9 0 例房颤患者11.06±3.42 pmol/L,29例正常对照组6.05±0.48 pmol/L,差异有统计学意义(P<0.05) 图2 冲击载荷Fig.2 Shock load (3) (4) 分别取不同刚度比kr(8~64),限位器安装间隙Gap(1~10 mm)变化,研究安装间隙Gap对系统的相对位移响应和加速度响应的影响规律,如图3、图4所示。 图3 相对位移响应曲线Fig.3 Relative displacement response curve 图4 加速度响应曲线Fig.4 Acceleration response curve 由图3可知:对于任意一刚度比kr,相对位移响应随安装间隙Gap的增加近似线性增大;且对于同一安装间隙,增大刚度比kr能够有效地降低相对位移响应,但这必然会引起加速度响应的骤然增大。 由图4可知:当刚度比kr<16,加速度响应会随安装间隙Gap的增加近似线性衰减;当刚度比kr≥16,加速度响应会随安装间隙Gap的增加呈先增大后减小的变化趋势,即存在一个特定间隙使得在该间隙下的加速度响应取得最大值,称这个特定间隙为“共振间隙”。为了更加清晰反映出“共振间隙”现象,将不同刚度比kr(16~64)下的加速度响应峰值连接起来,如图4中的曲线α所示。由此可知,“共振间隙”现象普遍存在,且随着刚度比的增大“共振间隙”逐渐向右移动。 分别取Gap为1 mm、3 mm、5 mm和8 mm四种初始安装间隙,限位器刚度比kr(4~64)变化,研究刚度比kr对系统的相对位移响应和加速度响应的影响规律,如图5、图6所示。 图5 相对位移响应曲线Fig.5 Relative displacement response curve 图6 加速度响应曲线Fig.6 Acceleration response curve 由图5可知,对于任意安装间隙,相对位移响应随着刚度比kr的增大而逐渐衰减,当kr<16时衰减迅速,当kr≥16时随刚度比增大衰减趋势逐渐变缓。 由图6可知,加速度响应随刚度比kr的增大而逐渐增大,与相对位移响应呈负相关;当kr<16,同一刚度比下,安装间隙越大,加速度响应越小;当kr≥16,随刚度比kr增大到某一值后会导致大安装间隙下的加速度响应反而超过小安装间隙下的加速度响应,例如对比图6中安装间隙Gap为1 mm与8 mm的两条曲线,当刚度比kr>24时,8 mm安装间隙的加速度响应反而超过了1 mm安装间隙的加速度响应,这是因为随着安装间隙的增大,要想产生“共振间隙”现象刚度比也要随之增大,所以安装间隙越大,随着刚度比增大就越接近达成“共振间隙”的条件,导致加速度响应急剧上升从而超过小安装间隙在此刚度比下的加速度响应。 综上由图3~图6可知,选配带限位隔振系统的限位参数时,在保证不影响系统的振动性能的前提下选择“共振间隙”左侧尽可能小的安装间隙;因为在“共振间隙”左侧随着安装间隙的减小,不仅使相对位移响应迅速减小,而且对于刚度比kr≥16加速度响应呈现迅速衰减趋势,对于刚度比kr<16加速度响应虽然略有上升,不过最大峰值都不大。其次,在确定限位器安装间隙之后,选择合适的刚度比kr,在保证相对位移响应不超过极限位移的条件下,使得加速度响应取得最小值。 为了验证上述仿真计算中限位器参数对带限位隔振系统冲击响应的影响规律的正确性,设计如图7所示的带限位隔振系统的试验装置。其中1为带限位隔振系统的底座,2为圆柱弹簧隔振器,3为中间质量块,用于模拟设备,4为限位器部分。通过改变限位元件的数量和调整垫片的厚度可以实现限位器刚度和安装间隙的改变,因此,该试验装置满足带限位隔振系统的功能要求。图8为带限位隔振系统实验装置在冲击试验台上的安装分布图,采用位移传感器和加速度传感器分别采集各工况中间质量块(设备)上的相对位移响应和加速度响应。 图7 带限位隔振系统试验装置Fig.7 Double limit vibration isolation system test device 图8 带限位隔振系统试验装置安装图Fig.8 Installation diagram of limit vibration isolation system test device 其中,图9、图10是第一组工况中安装间隙为5 mm的仿真计算与试验结果的相对位移响应,加速度响应的时域历程对比曲线。图11、图12是限位器安装间隙对带限位隔振系统冲击响应影响规律的仿真计算与试验对比曲线。图13、图14是限位器刚度比对带限位隔振系统冲击响应影响规律的仿真计算与试验对比曲线。 通过图9和图10可以看出,无论是相对位移响应,还是加速度响应,仿真计算与试验结果的的时域历程曲线高度重合,同时相对位移响应和加速度响应的最大峰值的误差也都在允许范围之内。这说明仿真计算具有较高的准确性,能够较好模拟出冲击试验中设备冲击响应的真实状况。 通过图11和图12可以看出,限位器安装间隙对限位隔振系统冲击响应影响,仿真计算与试验数据具有较好的一致性,在安装间隙Gap=4.5 mm附近,冲击试验的加速度响应同样出现了最大峰值,并且高于仿真计算结果。这说明“共振间隙”确实存在,对实际的冲击响应影响更大,所以避开“共振间隙”才是最佳选择。其中,第一组工况仿真数据与试验数据相对位移响应最大误差为1.9%,加速度响应最大误差为2.2%,都满足误差要求,验证了该组仿真计算的准确性。 通过图13和图14可以看出,限位器刚度比对限位隔振系统冲击响应影响,仿真计算与试验数据同样具有较好的一致性,相比仿真计算,随着刚度比kr的增大,试验获得的加速度响应增加的更快。其中,第二组工况仿真数据与试验数据相对位移响应最大误差为4.1%,加速度响应最大误差为3.4%,都满足误差要求,同样验证了该组仿真计算的准确性。 图9 仿真与试验的相对位移响应时域历程对比曲线Fig.9 Time domain comparison curve of relative displacement response between simulation and experiment 图10 仿真与试验的加速度响应对比曲线Fig.10 Time domain comparison curve of acceleration response between simulation and experimen 图11 仿真与试验的相对位移响应对比曲线Fig.11 Relative displacement response curve of simulation and experiment 图12 仿真与试验的加速度响应对比曲线Fig.12 Acceleration response curve of simulation and experiment 图13 仿真与试验相对位移响应对比曲线Fig.13 Relative displacement response curve of simulation and experiment 图14 仿真与试验的加速度响应对比曲线Fig.14 Acceleration response curve of simulation and experiment (1)通过对比仿真计算与试验结果,二者具有较好的一致性,说明本文采用的八参数可独立设置的计算模型能够准确反应带限位隔振系统各参数特性,非常适合带限位隔振系统的冲击响应的仿真计算。 (2)通过仿真计算与试验研究,发现了“共振间隙”的存在,其对相对位移响应影响不大,但会导致加速度响应的骤然上升,造成剧烈的二次冲击。文献[2]中分析安装间隙对无阻尼单限位隔振系统冲击响应的影响时,同样出现了类似“共振间隙”的现象。 (3)“共振间隙”现象产生的条件是,刚度比kr≥16,且初始安装间隙又不太小。并且随着刚度比的增大,“共振间隙”也会随之右移。 (4)在设计带限位隔振系统参数时,首要考虑安装间隙,在保证不影响系统振动性能的前提下,选择最小的安装间隙;在保证相对位移不超过极限位移条件下,选取合适的限位器刚度比使加速度响应最小。 (5)与冲击试验结果对比,仿真计算与试验数据具有良好的一致性,验证了仿真计算的准确性与合理性,证明了“共振间隙”确实存在,并对实际冲击激励下的加速度响应影响更大,不容忽视,所以合理匹配限位器参数,避开“共振间隙”才是最佳选择。
1.3 冲击输入载荷的确定
2 限位器参数对带限位隔振系统冲击响应影响分析
2.1 限位器安装间隙对系统冲击响应的影响


2.2 限位器刚度比对系统冲击响应的影响

3 冲击试验与仿真结果对比分析
3.1 带限位隔振系统试验装置


3.2 冲击试验与仿真计算对比算例


4 结 论
