基于衰减余弦字典和稀疏特征符号搜索算法的轴承微弱故障特征提取
2019-11-20周浩轩刘义民
周浩轩,刘义民,刘 韬
(昆明理工大学 机电工程学院,昆明 650504)
滚动轴承作为现代工业设备中装备最多、应用最广的核心零部件,其能否正常工作关乎设备的正常运转,统计显示,滚动轴承是引起设备故障的重要原因之一,约有30%的旋转机械故障与滚动轴承的损坏相关联。轴承的损伤故障主要是点蚀和剥落[1],基于振动信号的分析从而提取其故障特征频率是目前较为有效的方法,但早期故障信号由于故障尺寸较小,噪声干扰极大,其故障特征成分十分微弱,导致故障特征难以凸显,提取难度较大。获取有效的早期轴承故障特征提取方法是目前研究的关键。传统的时域参数分析方法如基于信号的平均值、和频域分析方法如包络谱分析[2-3]、倒谱分析[4]等,这些传统的分析方法都易受到噪声的干扰,对于强噪声信号和早期轴承故障信号特征提取效果不好。而具有多分辨分析能力的小波分析[5-7]也会由于其基函数冗余度不够、与故障成分匹配度低而不能有效、准确地表征强背景噪声下的故障信号。相比基于稀疏表示的信号过完备稀疏表示方法具有更为灵活、抗噪声能力更强的特点。稀疏表示中的匹配追踪[8](MP)算法由于其获得的往往是局部最优解,并不能得到信号的全局最优稀疏表示,对于求解信号的精确稀疏表示不是一个最好的方法。基于基追踪[9]优化方法的稀疏表示已经有许多学者做了较多的工作,其中图像处理领域运用较为广泛[10-14]。将稀疏表示理论运用于现代故障诊断领域特别是轴承故障信号是近年来的一种较为新颖的研究方向,可以运用稀疏表示算法中过完备原子的冗余性完整精确地表达待分解信号,以达到去噪、增加信号稀疏度的作用,文献[15]以Laplace小波作为过完备原子库基函数结合稀疏MP算法在含噪信号中提取出了故障频率,文献[16]通过匹配追踪算法与快速独立分析法相结合对轴承混合故障进行了故障信号的分离与提取。文献[17]通过运用并联基追踪的方法对早期齿轮故障信号进行了特征提取。文献[18]提出了基于复杂度谱和复杂度谱熵的稀疏MP算法来准确提取低信噪比下滚动轴承信号的故障特征的方法,取得了较好的效果。文献[19]将小波包变换(WPT)与稀疏表示理论结合并应用于实际轴承箱故障模式识别。文献[20]提出基于稀疏移不变编码的基函数学习字典的稀疏表示方法,并应用于轴承与齿轮的故障分析中,取得了一定的效果。
以上方法在处理低信噪比故障轴承信号时存在过完备冗余原子库与故障特征匹配度不高,基于稀疏匹配追踪算法的信号去噪方法计算精度较低等问题。而传统基追踪算法也存在计算复杂度高、计算效率低等问题,导致对超低信噪比故障轴承信号的特征提取鲁棒性不足。针对以上问题,本文提出基于与轴承故障信号特征高度匹配的衰减余弦原子(Attenuated Cosine Dictionary)与快速符号搜索基追踪算法(Feature-Sign Search)相结合的稀疏表示特征提取算法(ACFS),并通过分析仿真信号与实测轴承早期微弱故障信号进行了算法验证,通过与原始信号包络解调算法、基于小波包的常规基追踪去噪算法(BPDN)相比较,显示该方法可以在强噪声干扰信号中快速、精确的提取出故障特征频率。
1 基于过完备原子库与基追踪的优化算法
1.1 优化算法
在稀疏表示理论中,基本的算法包括贪婪算法中的匹配追踪(Matching Pursuit,MP)、正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法,松弛优化算法中的基追踪(Basis Pursuit,BP)、FOCUSS(Focal Underdetermined System Solver)算法等,其中基追踪算法(Basis Pursuit)与匹配追踪(Matching Pursuit)应用较为广泛,基追踪相比匹配追踪算法具有所求解为全局最优解、计算精度高等特点,在微弱故障检测中具有较好的优势[21]。
稀疏表示的目的是将输入向量近似表示为少数“基向量”的加权线性组合。该基向量可以捕捉输入信号中与之匹配度高的成分,输入信号X∈Rk可以通过基向量a与稀疏系数s表示
X=∑jajsj
(1)
同:
X=As
(2)
其中矩阵A={a1,a2,…,aj},系数s={s1,s2,…,sj}T,而信号X的稀疏表示即为求解以下问题
(3)
当信号中含有一定量噪声时,其模型如下
y=x+σz
(4)
式中:y为含噪信号;x为真实纯净信号;z为噪声,σ为噪声方差。
在稀疏表示理论中,可以认为去噪重构后的误差X-∑bjsj服从均值为0方差为σ的高斯分布,为选取出去噪最优稀疏系数sj,则最优稀疏系数分布可以通过下式进行约束[22]
P(sj)∝exp(λφ(sj))
(5)
式中:λ为正则化参数,控制着重构残余部分;φ(.)为正则化方法,由于l0范数正则化方法为NP难问题,通常选取l1范数作为稀疏性度量函数。参数λ可以设为
(6)
参数p为过完备字典的原子数,σ为噪声方差。在实际运用中需要对噪声方差进行估计,由于轴承信号噪声普遍较大,权衡算法效率,本文选用文献[23]提出的基于小波域的噪声方差估计方如式(7),MAD是高频子带小波系数幅度的中值。
根据Donoho理论[24],基于基追踪优化方法的去噪理论可以转化为求解下式
(8)
同,
(9)
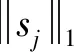
步骤1 初始化稀疏系数sj=0及其对应的符号集合θj=0,其中θj∈{-1,0,1},active set:{}。
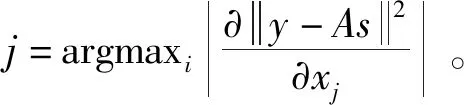

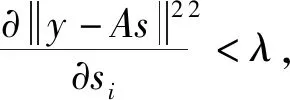
步骤3 特征符号搜索
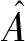
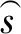
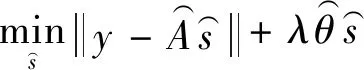
(10)
(11)
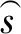
步骤4 检查最优停止条件
条件① 非零系数的最优性条件
(12)
条件② 零系数的最优性条件
(13)
如果条件①不满足则进入步骤3,否则检查条件②。
如果条件②不满足则进入步骤2,否则输出系数s,算法结束。
1.2 过完备原子库
稀疏表示理论中的另一个重要部分就是过完备原子库,选择、构造与待重构信号匹配度高的原子库是稀疏表示的重点。常见的过完备原子字典有分析字典和学习字典两大类,学习字典基于对原始信号的学习而构成,对于训练信号噪声较大的情况,学习字典容易将部分噪声学习到过完备字典中,影响低信噪比信号的去噪效果,本文重点介绍分析字典同时构造与轴承信号高度匹配的分析字典。
分析字典包括Fourier字典、Gabor字典、Symlet字典、Dirac字典、余弦字典等,其中Symlet字典与冲击信号的特征具有一定的匹配度,可以用作一般信噪比较高的轴承故障信号的去噪分析,对于较低信噪比轴承故障信号尤其是早期故障轴承信号,由于其原子特征匹配度不高,故不能有效的提取出故障频率,该原子库对于早期微弱轴承故障信号的表现将在后文结合普通BPDN方法对其进行分析比较。
分析轴承点蚀故障的动力学模型后,这里选择构造与轴承故障信号匹配度高的基于单边衰减余弦原子的过完备原子库,其表达式为
(14)
式中:fn,ξ,t,τ分别为过完备原子库的参数,fn,ξ为原子库原子的形态参数,决定原子的形态特征,t,τ为原子库原子的时移参数,决定原子在原子库时间轴上的分布。由于冲击在时域是暂时的,所以其在频域范围内具有宽带特性,由此会激发系统的共振,所以设置fn为故障冲击激发的系统共振频率以更好反映冲击特性。ξ为阻尼系数,t为原子基函数的时间变量,τ为原子的时移参数。
由于故障发生时共振频率处携带的能量较大,反映在频谱中高频带频率幅值高,故可以通过寻找频谱中的峰值频率来作为fn的取值。分析轴承故障冲击波形可以确定参数ξ,选取该参数需要保证原子基函数在自身长度内时域幅值衰减到0。参数τ设置为采样率的倒数以保证过完备原子库在整个信号长度上的冗余性,以上四个参数张成了基于衰减余弦波的过完备原子库。将张成的与轴承故障高度匹配的过完备原子库同基于基追踪优化方法的特征符号搜索算法相结合,求出信号在过完备原子库中的稀疏系数,得到其重构稀疏表达,从而达到去除噪声的作用。
算法流程图如图1所示。
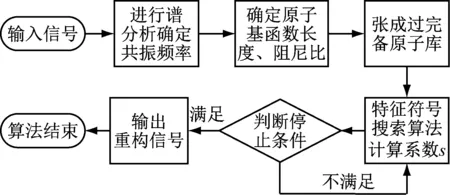
图1 算法流程图Fig.1 Algorithm flow chart
将去噪重构后的信号进行Hilbert包络分析便可得到被噪声掩盖的故障特征频率,进而完成强噪声中轴承故障特征的提取。
2 算法仿真分析
由于在轴承早期故障中,内圈发生故障的概率较大,现构造加入一定信噪比噪声的轴承内圈仿真信号,以验证算法可靠性。轴承内圈仿真信号表达式如下[25-26]
(15)
其中冲击幅值A取2 m/s2,CA是幅值随机常数(CA>A0),采样频率fs为25 600 Hz,系统共振频率fn为4 000 Hz,内圈故障特征频率fi(105 Hz),s(t)是点蚀故障引起的冲击,T是冲击周期,fr为主轴转频,B是冲击信号的衰减系数,n(t)是随机噪声。现加入SNR为-5 dB的高斯白噪声。原始信号与含噪信号如图2(a)、(b)所示。
计算含噪信号频谱得其频率峰值为4 005 Hz,为了满足原子库各原子的完整性和单个原子长度范围内幅值衰减为0的原则,根据单个冲击持续时间长度确定基函数点数为244,阻尼比ξ为800。平衡原子库的冗余性和计算效率,时移参数τ设置为采样率的倒数。计算得到重构信号并对其进行Hilbert解调得到重构信号包络谱如图3(c)。可以看到重构信号基本去除了噪声的干扰,得到的包络谱图可以清晰的看到故障特征频率105 Hz、转频边带及倍频成分。

(a)无噪轴承内圈仿真信号

(b)SNR=-5 dB时域波形图2 轴承内圈故障仿真信号Fig.2 Bearing inner ring fault simulation signal
将相同内圈仿真信号信噪比降低到-15 dB。根据同样的方法计算得到重构信号、重构包络,如图4所示。

(a)仿真信号频谱

(b)重构信号时域波形

(c)重构信号包络谱图3 SNR=-15 dB仿真信号频谱与基于ACFS算法的计算结果Fig.3 Spectrum of SNR=-15 dB simulated signal and calculation result based on ACFS algorithm

(a)SNR=-15 dB时域波形

(b)重构信号时域波形

(c)重构信号包络谱图4 基于ACFS算法的SNR=-15 dB仿真信号计算结果Fig.4 SNR=-15 dB simulation signal calculation result based on ACFS algorithm
进一步降低仿真信号的信噪比到-18 dB,信号时域波形与原始包络如图5、6所示。作为对比,本文给出了稀疏表示特征提取算法中常用的基于Symlet小波包的BPDN方法特征提取结果,重构信号与包络谱见图7。基于本文ACFS算法特征提取的结果如图8所示。
从图8可以看到在极低信噪比输入信号下,ACFS仍能提取出轴承内圈故障频率(105 Hz),此时原始包络解调的方法已经无法提取出故障频率,同样地基于Symlet8小波包原子库的BPDN方法也无法有效提取出故障特征频率。

图5 SNR=-18 dB仿真信号时域波形Fig.5 Time domain waveform of SNR=-18 dB analog signal

图6 仿真信号原始包络谱Fig.6 Original envelope spectrum
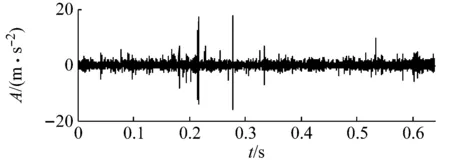
(a)重构信号

(b)BPDN方法重构信号包络谱图7 基于Symlet小波包BPDN方法的特征提取结果Fig.7 Feature extraction based on symlet wavelet packet BPDN method
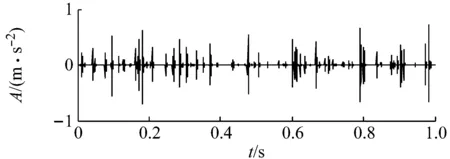
(a)重构信号时域波形

(b)重构信号包络谱图8 基于ACFS算法的SNR=-18 dB仿真信号计算结果Fig.8 SNR=-18 dB simulation signal calculation result based on ACFS algorithm
三种方法的计算效率如表1所示。
表1 SNR=-18 dB仿真信号的三种特征提取方法计算效率
Tab.1 Time-consuming calculation of three feature extraction methods based on SNR=-18 dB simulation signal

原始包络BPDNACFS0.007591s17s0.6018s
综上,可以知道本文所提算法在计算准确度、计算效率两方面对比普通包络和BPDN方法都有较大优势,其能够在信噪比低至-18 dB的输入信号中准确高效地提出轴承的故障频率。说明了其在高背景噪声下极强的适应能力。
3 轴承全寿命早期故障信号分析
仿真的轴承故障信号与实际轴承的失效结果有所不同,轴承的早期故障由于其故障点尺寸较小,冲击信号并不明显,噪声源更为复杂等原因。运用普通特征提取方法提取其早期故障特征尤为困难,现基于本文所提出的ACFS算法对轴承早期故障特征提取进行验证。
实验数据通过轴承加速疲劳寿命实验获得,试验台使用杭州轴承试验研究中心有限公司ABLT-1A轴承寿命试验机,结构如图9,实验对象为NSK公司6205深沟球轴承,数据采集系统基于Labview软件平台开发。采样率为51 200 Hz,转速为3 000 r/min(转频fr=50 Hz),从开始实验到轴承失效一共持续了269小时,均方根RMS达到21/Vrms,轴承完全失效,拆解轴承发现内圈发生点蚀剥落。NSK6205深沟球轴承内外圈理论故障频率为:外圈故障fo=179.25 Hz,内圈故障fi=270.25 Hz。计算得到全寿命数据RMS趋势图与早期故障区间放大图如图11、12所示。选取图11中位置1的点所在信号数据。其时域波形如图13所示,计算其原始包络与基于Symlet小波包的BPDN结果如图14、15所示。

图9 ABLT-1A轴承寿命试验机Fig.9 ABLT-1A bearing life tester

图10 6205轴承内圈故障拆解图Fig.10 6205-type bearing inner ring breakdown diagram

图11 6205轴承全寿命周期的有效值RMS变化趋势Fig.11 Trend of RMS change over 6205 bearing life cycle

图12 6205轴承全寿命周期早期故障放大(部分)Fig.12 6205-type bearing life RMS trend chart (partial)

图13 时间点1的早期故障信号时域波形Fig.13 Time-domain waveforms of early failure signals at point 1

图14 时间点1的早期故障信号原始包络谱Fig.14 Early failure signal original envelope at point 1

图15 基于BPDN方法重构时域波形Fig.15 Reconstruction of the time-domain waveform based on the BPDN method
通过分析频谱图16(a)发现,3 000 Hz到4 000 Hz这一段共振带能量较大,选取该共振带峰值频率3 717 Hz作为原子库参数fn,阻尼比设置为1 540,原子库原子基函数点数为286点。计算得到重构信号、重构包络谱如图16(b)、(c)。三种方法针对一秒信号计算效率如表2所示。
基于本文ACFS算法的重构信号包络谱可以清晰的看到故障频率fi=269 Hz,对比原始包络与基于Symlet8小波包字典的基追踪去噪效果,原始包络故障频率并不明显,而小波包基追踪已经不能提取出微弱的冲击特征了,反而提取出了与转频相关的正弦波。分析这是由于基于Symlet小波的过完备原子库与微弱故障特征匹配度不高,故在故障信号能量极低的情况下,更容易匹配到其他成分。进一步表明该方法对于实际轴承早期微弱故障信号提取并不适用。结合计算效率与结果准确性,可以认为ACFS算法实现了强背景噪声下故障频率的高效、准确地提取。

(a)时间点1的早期故障信号频谱

(b)重构信号时域波形

(c)重构信号包络谱图16 时间点1的早期故障信号ACFS算法计算结果Fig.16 Result of ACFS algorithm calculation of early failure signal at point 1
表2 基于早期故障信号的三种特征提取方法计算效率
Tab.2 Time-consuming calculation of three feature extraction methods based on early failure signals

原始包络BPDNACFS0.011032s876.6s8.1s
现对全寿命数据早期故障区间中更微弱的信号进行分析,选取图12中点2位置所在信号数据进行分析。所张成原子库的参数设置与上文相同,其早期故障时域波形和ACFS算法计算结果如图17所示。
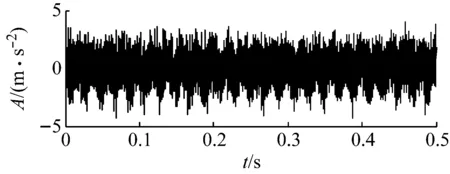
图17 时间点2的早期故障时域波形Fig.17 Early fault time domain waveform at point 2
对比图18与图19(c)可以看到,对于微弱早期故障信号,ACFS算法依然可以提取到内圈故障频率fi=269 Hz,此时故障特征能量已经极低,对原始信号进行包络解调已无法提取内圈故障频率fi。对比结果表明本算法对于强噪声干扰的轴承早期微弱故障信号有着较强的鲁棒性与较高冗余度。

图18 时间点2的早期故障信号原始包络谱Fig.18 Early fault signal original envelope spectrum at point 2

(a)重构信号时域波形
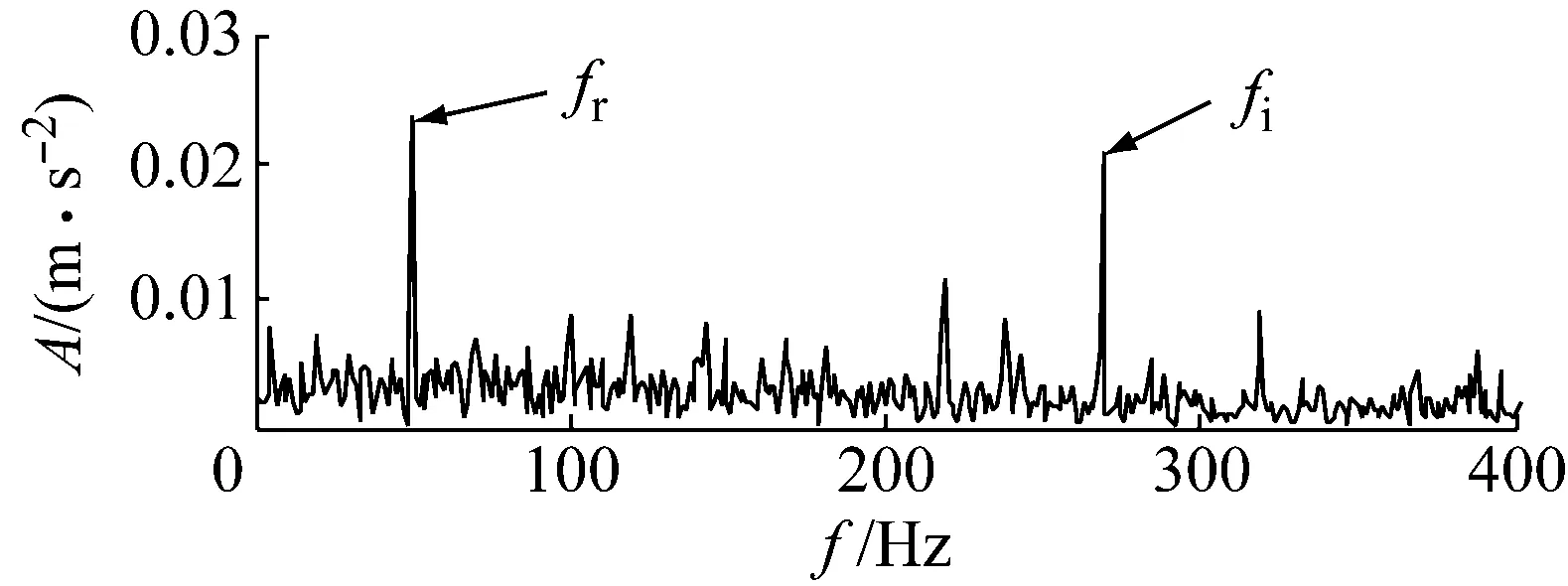
(b)重构信号包络谱图19 时间点2的早期故障信号ACFS算法计算结果Fig.19 Result of ACFS algorithm calculation of early failure signal at point 2
4 结 论
本文通过构造与轴承点蚀剥落故障信号高度匹配的过完备冗余原子库,将稀疏表示特征符号搜索算法与之相结合并运用在强噪声干扰下的轴承故障特征提取中。仿真和实验分析表明,结合了基追踪方法全局最优准则的特征符号搜索算法可以通过过完备原子库高效地求得轴承故障信号最优稀疏表示系数,进而达到去除强噪声的作用,对重构的稀疏信号进行包络分析可以有效地提取强背景噪声干扰下的早期轴承故障特征。
