含时滞反馈控制的直齿圆柱齿轮主共振分析
2019-11-20石慧荣赵冬艳李宗刚张军平
石慧荣,赵冬艳,李宗刚,张军平
(兰州交通大学 机电工程学院,兰州 730070)
直齿圆柱齿轮传动以其结构紧凑、传动准确、经济性好等特点被广泛应用于汽车、机床、船舶、航空等工业生产领域,其传动性能决定了应用装备的使用性能,因此对齿轮传动的减振控制具有重要实际意义。然而由于齿轮传动具有比较复杂非线性行为,所以应用中很难确定与之匹配的控制参数,因此控制参数对齿轮系统稳定性的影响已成为该领域的一个重要课题。
齿轮传动系统非线性行为已经被广泛研究,主要集中在侧隙、时变啮合刚度、载荷波动和制造装配误差等对传动的影响上。Moradi等[1]利用多尺度法分析了含间隙的直齿圆柱齿轮系统的动力学特性,结果表明在特定参数下主共振、超谐波和亚谐波共振均会出现跳跃和不稳定现象。Lu等[2]利用数值计算法研究了影响直齿圆柱齿轮传动非线性特性的因素,结果表明轻载时更容易导致系统出现混沌,系统参数的合理匹配能提升其传动的稳定性。Singh[3]利用Floquet定理分析了考虑齿面摩擦作用的斜齿轮扭转传动特性,表明摩擦作用力对斜齿传动影响较小。张微等[4]利用多尺度法分析了直齿圆柱齿轮传动的稳定性,结果表明当轮齿啮合频率接近和型共振频率时,系统会发生参数共振,存在着不收敛的无界解。魏莎等[5]运用区间谐波平衡法分析了考虑区间系统参数的齿轮副非线性系统动态响应,研究表明侧隙、阻尼和载荷参数对系统动态特性具有较大影响。为了提升齿轮系统的传动性能,一些主动减振方法也受到一些学者的关注。Chen等[6]提出一种改变啮合刚度的齿轮传动主动减振方法,并验证了其有效性。Li等[7-8]提出了一种利用压电堆装置主动控制齿轮转子支撑装置振动从而抑制齿轮传动振动的方法,并实验验证了控制方法的有效性。李以农等[9]对齿轮传动压电堆作动减振提出一种自适应算法主动控制方案,并对其进行了实验验证。
综上所述,现有的研究主要关注传动系统内部参数对系统非线性行为的影响或特定控制方法的减振作用,综合考虑控制参数和齿轮系统参数的动力学行为研究还比较少。本文为了有效减小直齿圆柱齿轮系统由于外载荷激励波动和时变啮合刚度引起的振动,对系统施加时滞反馈控制,并采用多尺度法分析齿轮系统载荷波动和啮合刚度波动对主共振的影响,研究时滞反馈控制参数对齿轮传动动态特性的影响。
1 时滞反馈直齿圆柱齿轮传动系统模型
齿轮传动系统由于制造误差、装配误差、侧隙、时变啮合刚度和齿面接触变形等因素的影响,啮合齿对间的作用力很难确定,因此齿轮系统的动态特性比较复杂,但本文主要研究啮合刚度变化和外加激励载荷对系统传动的影响,因此可以将其简化成一个单自由度系统[10],假定轴承和轴的支撑刚度远大于齿轮的啮合刚度,此时可以近似认为齿轮与支座刚性连接,所以只考虑扭转自由度,由此可得齿轮系统的动力学方程为
(1)
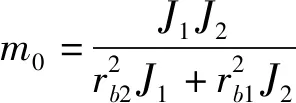
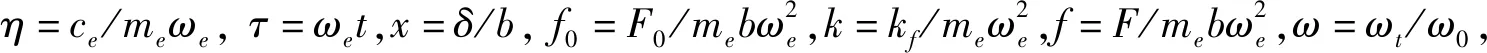
(2)
无量纲化的侧隙函数为
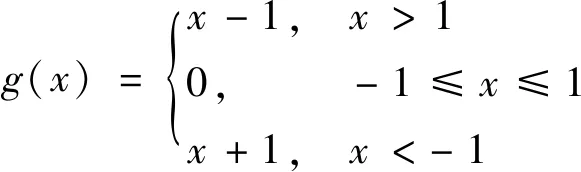
(3)
根据文献[1]对齿轮传动的研究方法,可以将侧隙函数近似为
g(x)=d1x+d2x3=d1(x+d0x3)
(4)
其中d0=d2/d1,当d1=0.463,d2=0.016 04时,拟合均方差0.21,确定系数为0.989 8,此时式(4)的侧隙函数能够较精确地反映分段函数(3)所表示的轮齿接触、脱齿和齿背冲击现象,并且使系统光滑化。将式(4)代入式(1)中,齿轮系统转变为一种类Mathieu-Duffing振子,并考虑对齿轮支撑系统施加时滞位移速度反馈控制,根据文献[13]可以得到时滞反馈齿轮传动系统的数学模型为
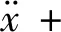
(5)
2 时滞反馈齿轮传动系统的多尺度法分析

x(t)=x0(T0,T1,…)+εx1(T0,T1,…)+
ε2x2(T0,T1,…)+…
(6)
x(t-τ)=x0τ(T0,T1,…)+εx1τ(T0,T1,…)+
ε2x2τ(T0,T1,…)+…
(7)

(8)
(9)
为了获得有效的近似解,必须使啮合阻尼、啮合刚度波动量、非线性项、激励载荷与控制增益为同阶量,因此重新标定系统参量η=2εμ,k=εk,d0=εd0,f=εf,g1=εg1,g2=εg2,并将偏导算子(8)和(9)以及近似解(6)和(7)代入齿轮的系统方程(5)中,令ε0和ε1的系数相等可得
(10)

g2D0x0τv-2μD0x0-2D0D1x0-
(11)
Aτ(T1)=Aτ(T1-ετ)≈A(T1)-ετA(T1)+…
(12)
同时令cosωτ=(eiωτ+e-iωτ)/2,将x0和式(12)代入式(11)可得
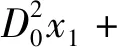
d2A2[Ae3iω0T0+3f0e2iω0T0]+
(13)
式中,cc表示前面各项的共轭。式(13)可能存在的多种谐波响应分别为
(1)微共振:ω≈0;
(2)主共振:ω≈ω0;
(3)次谐波共振:ω≈2ω0。
3 时滞反馈齿轮系统的主共振稳定性分析
本文主要对齿轮传动系统的主共振特性进行分析,引入激励频率失调参数σ,使得
ω=ω0+εσ
(14)
为了消去永年项,令上式中含有eiω0T0的系数为零,可以得到
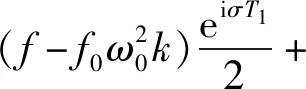
iω0A(g2e-iω0τv-2μ)
(15)
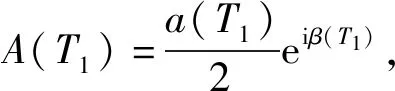
(16)
(17)
其中

(g2ω0sinω0τv+g1cosω0τd)
N=(2ω0μ-ω0g2cosω0τv+g1sinω0τd)
(18)
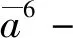
(19)
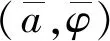
(20)
因此矩阵的特征值方程为
(21)
要使特征值λ具有负实部保证系统的稳定性,式(21)必须满足以下条件
N>0
(22)
4 主共振的数值分析
针对简化的齿轮传动系统,初始传动参数由表1给出,无量纲化后的静载荷f0=0.215,载荷波动幅度f=0.2,啮合刚度波动幅值k=0.2,啮合阻尼μ=0.1,小参数ε=0.02,位移和速度反馈增益g1=g2=0.1,时滞为τd=τv=T/9,其中T=2π/ω0,后续分析中未作特定说明,各参数均为初始参数。为了更加全面了解齿轮传动系统的动态特性,数值分析主要探讨外加激励波动、啮合刚度波动、迟滞反馈参数对齿轮系统主共振的影响。

表1 齿轮参数表Tab.1 Gear parameters
4.1 载荷波动对传动的影响
当g1=g2=0时无时滞反馈作用,此时载荷波动幅度f对主共振的影响如图1所示,图1(a)为不同外加载荷波动f时齿轮系统的幅频变化关系,图中灰色部分为不稳定振动分支,由图可以看出,当外加激励波动f逐渐增大时,主共振幅值增大,灰色不稳定分支增加,系统的定性变差,在较大的f作用下才会引起振幅的“跳跃”。图1(b)表明当激励频率ω小于齿轮系统的主共振频率时,振幅随f的增大逐渐增大,在ω大于主共振频率进入不稳定频带后出现多个振幅分支,从而引起系统的不稳定,这也称之为滞后现象。因此在接近主共振的齿轮传动系统中应注意控制啮合齿对的载荷波动,保证传动的稳定性和可靠性。

(a)

(b)图1 载荷波动对振幅影响Fig.1 The effect of load fluctuation on the amplitude
4.2 啮合刚度波动对传动的影响
同样在g1=g2=0时,啮合刚度波动k对主共振影响如图2所示,由图2(a)可以看出,随着啮合刚度波动k的增加,主共振的最大稳态幅值逐渐减小,不稳定分支也不断缩聚,因此一定啮合刚度波动会缩减主共振稳态幅值,提高主共振的稳定性,但k对主共振稳态幅值的影响比较小。图2(b)表明当激励频率ω进入不稳定区域后,k在一定范围内变化会导致齿轮系统主共振的失稳,而且ω越大,触发主共振不稳定的最小k越小,而且较小的k亦可诱发系统的大幅振动,导致主共振稳态幅值的多值性,引起主共振的不稳定。实际传动中k越小,传动的稳定性较好,但在接近主共振频率时,虽然啮合刚度波动幅度较小仍然可能引起系统的大幅振动。
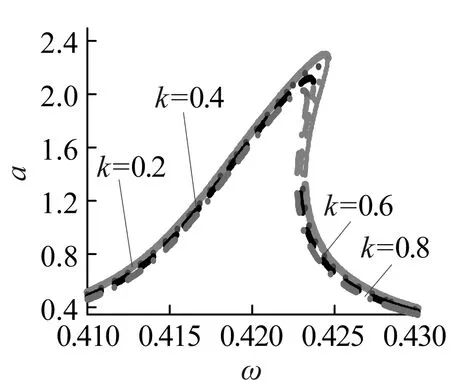
(a)
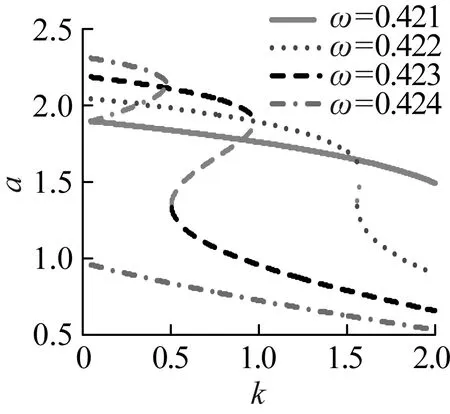
(b)图2 啮合刚度波动对振幅影响Fig.2 The effect of mesh stiffness on the amplitude
4.3 控制参数对传动的影响
由于齿轮传动系统的外加载荷波动和啮合刚度波动会引起系统传动的不稳定,因此为了减小系统振动,提升运转稳定性,对其施加时滞反馈控制,特定控制参数变化时齿轮系统的主共振特性由图3和图4给出。
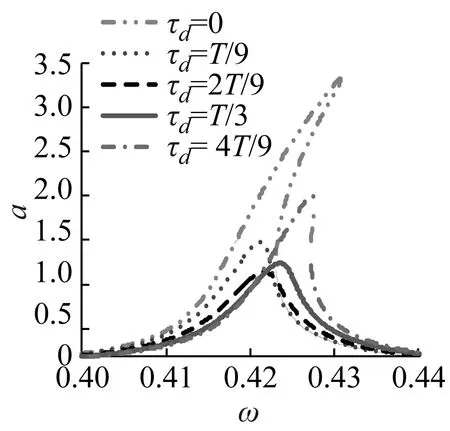
图3为不同参数对主共振幅频曲线的影响。在图3(a)中,当位移控制增益g1逐渐增大时,主共振幅频曲线向左偏移,主共振峰值频率减小;当g1=-0.1时使主共振稳态幅值大幅增加,灰色不稳定分支大幅扩展,因此特定的g1可能导致主共振稳定性变差;而且合理的选取g1可以有效缩减主共振稳态幅值,增加系统的稳定性,如g1=0.2时,稳态幅值仅为0.94。图3(b)表明随着速度控制增益g2由负→正逐渐增大,主共振稳态幅值逐渐增大,而且当g2较大,如g2=0.2时,会导致系统的不稳定,因此负速度反馈增益g2能够使主共振稳态幅值有效减小,增加系统稳定性。由图3(c)可以看出,控制系统位移时滞τd在0~T/2内变化时,主共振稳态幅值不断波动,特定的τd会导致主共振的不稳定,只有在τd接近T/4时齿轮系统的主共振稳态振幅值最小,此时系统具有较好的稳定性;而且也注意到随着τd的增加,主共振骨架曲线右移,使主共振频率增大。图3(d)表明在当前系统中随着速度时滞τv增加稳态幅值不断减小,不稳定灰色分支逐渐缩聚,在τv=T/2时对主共振具有较好减振性。

(a)
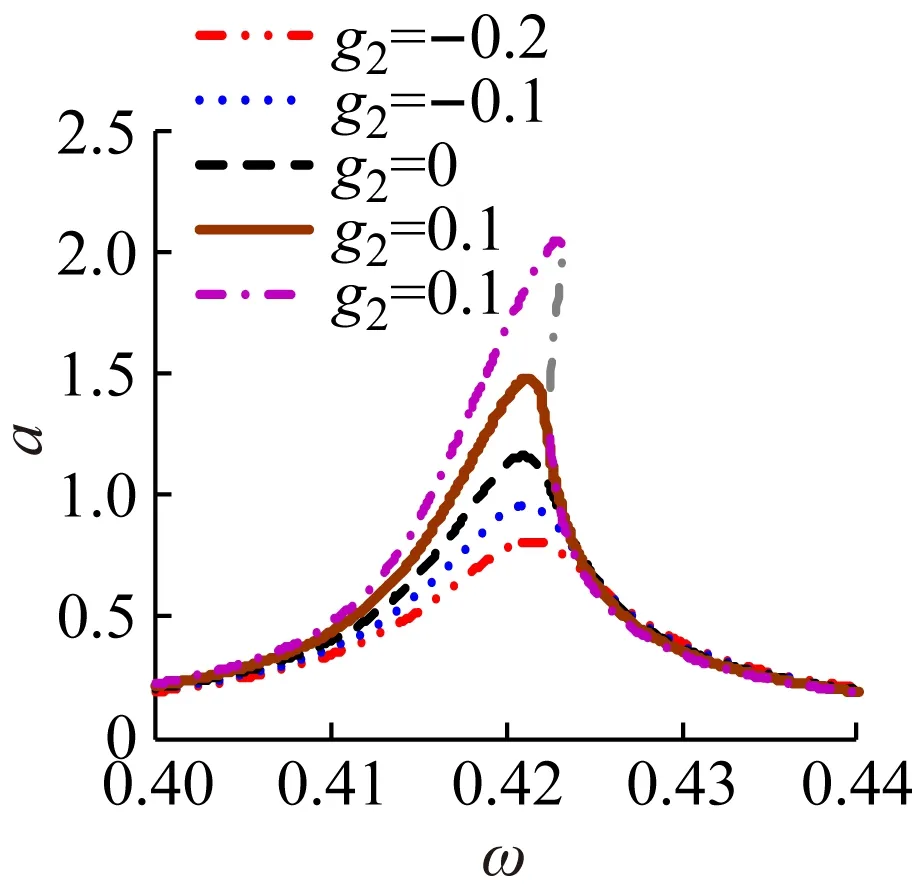
(b)
(c)

(d)图3 不同控制参数对应的主共振幅频响应Fig.3 The frequency response in different control parameters

(a)
(b)

(c)

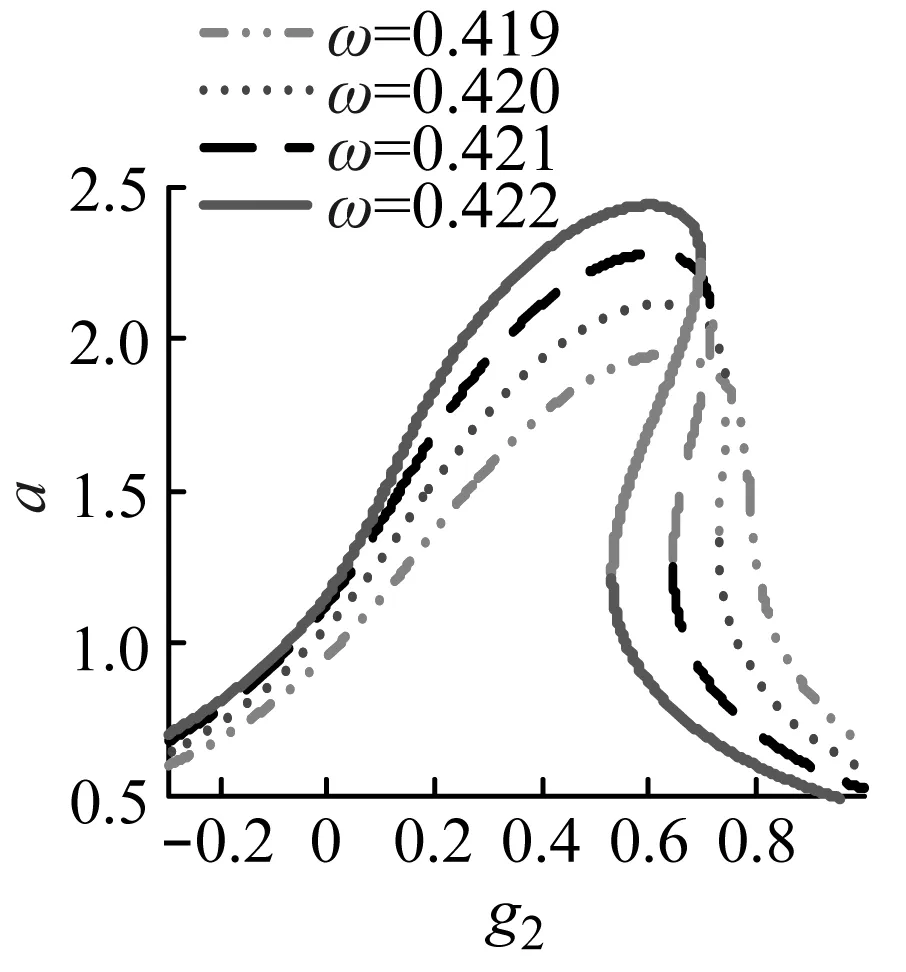
(d)图4 控制参数对振幅的影响Fig.4 The effect of control parameters on the amplitude
图4是各时滞控制参数对主共振稳态幅值的影响曲线。其中图4(a)表明位移控制增益g1在一定范围内取值可能导致主共振稳态幅值大幅增加,当ω超过临界频率后,ω越大g1导致主共振不稳定的可能性越大;随着ω的增加触发主共振不稳定的最小g1减小,而且对于当前系统g1的绝对值在零附近时更易诱发主共振的不稳定。图4(b)说明速度控制增益g2在一定范围内取值也会使主共振稳态幅值增大,随着ω的增加,g2导致主共振失稳的可能性增加,同时也注意到本系统中g2为正更易导致直齿轮主共振的失稳。在图4(c)中可以看出,当ω小于临界频率时,主共振稳态幅值随位移时滞τd增加而减小,不会引起主共振的不稳定;当ω超过临界频率后,τd在一定范围内会导致主共振的稳定性变差,ω越大τd导致主共振不稳定的可能性越高,而且随着ω的增加触发主共振不稳定的最小时滞减小。图4(d)表明在ω小于临界频率时,τv不会影响主共振的稳定性,此时只有τv较大的才会使主共振稳态幅值有效缩减;当ω大于临界频率后,类似于位移时滞对稳态幅值的影响,ω越高τv诱发齿轮系统的不稳定运动的可能性越大,但稳态幅值随τv的变化趋势与位移时滞不同。
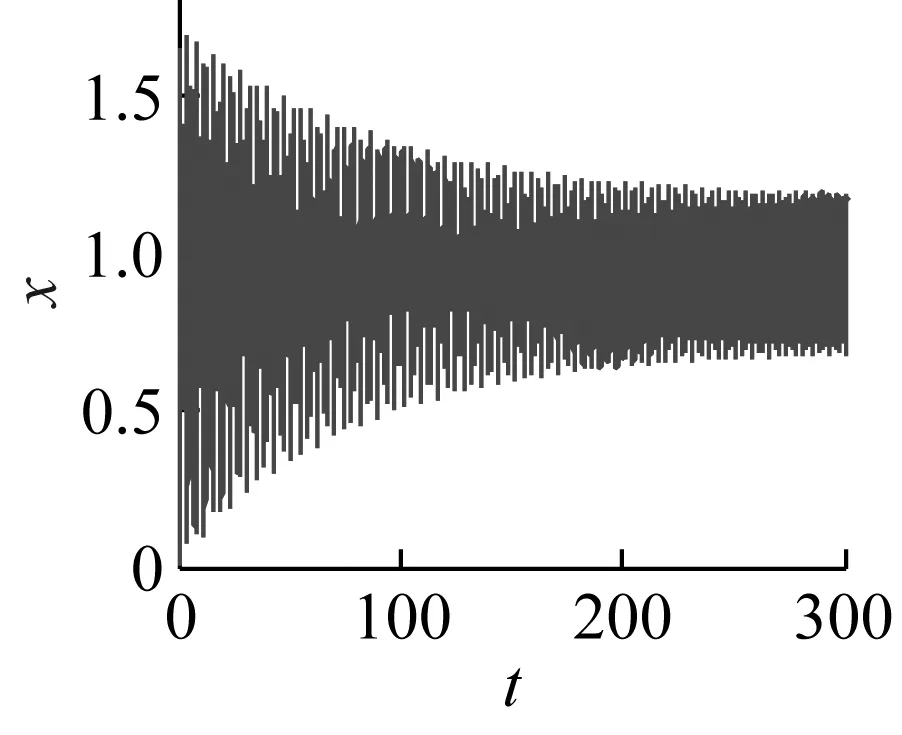
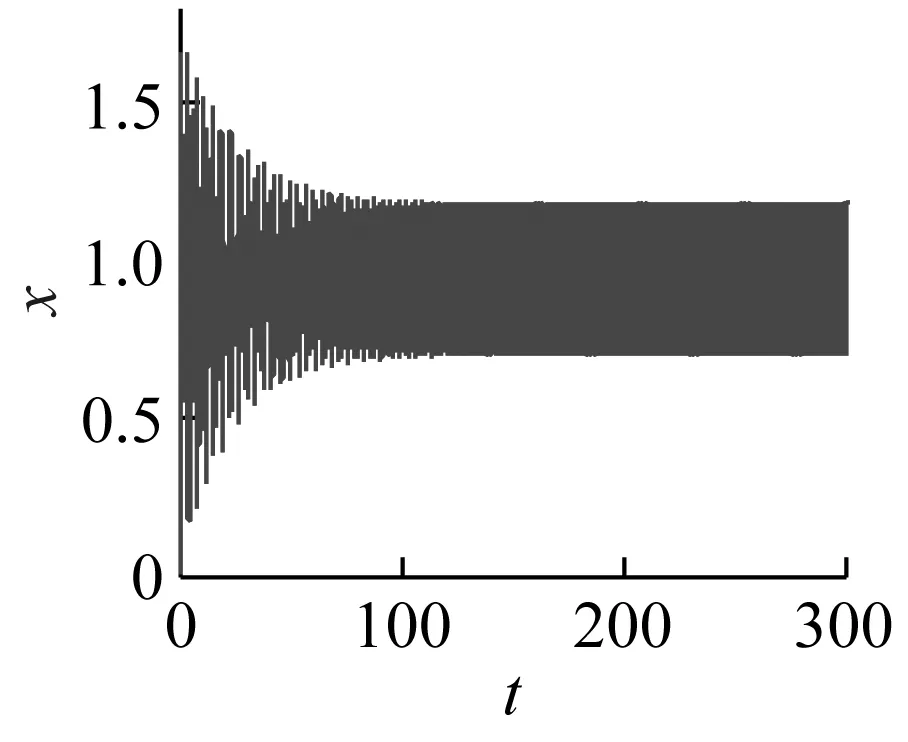
当激励频率ω=0.422 6时,利用Runge-Kutta法对式(6)进行数值求解,可以得到图5(a)~(c)分别是g1=g2=0,τd=τv= 0、g1=0.2,g2=-0.2,τd=T/4,τv=T/2和g1=-0.2,g2=0.2,τd=τv=T/20时对应的时域响应和相图。由图5(a)可以看出,由于此时主共振不稳定,齿轮系统传动误差稳态在一定范围内波动;当采用合理的时滞反馈控制后如图5(b)所示,动态误差快速收敛到封闭曲线上;但是在图5(c)中,控制参数选取偏离理想值时,时滞反馈控制反而导致齿轮系统传动误差严重偏离稳定解,使动态误差大幅增加,稳定性变差。因此齿轮系统的时滞反馈减振控制,必须选取匹配的控制参数,确保控制方法的有效性。
(a1)
(b1)
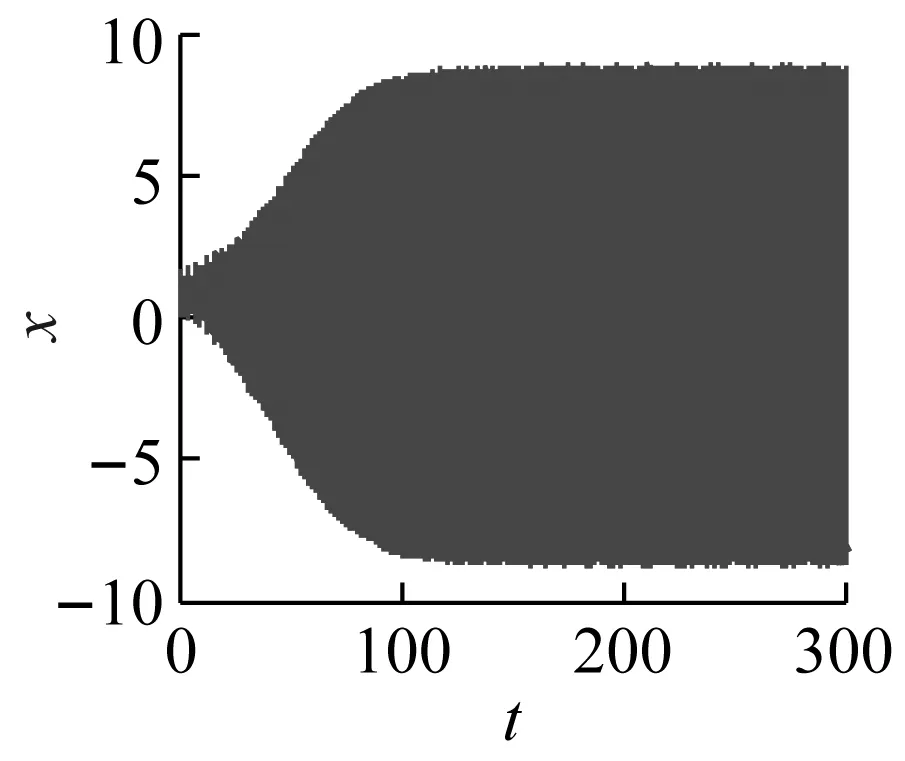
(c1)

(a2)
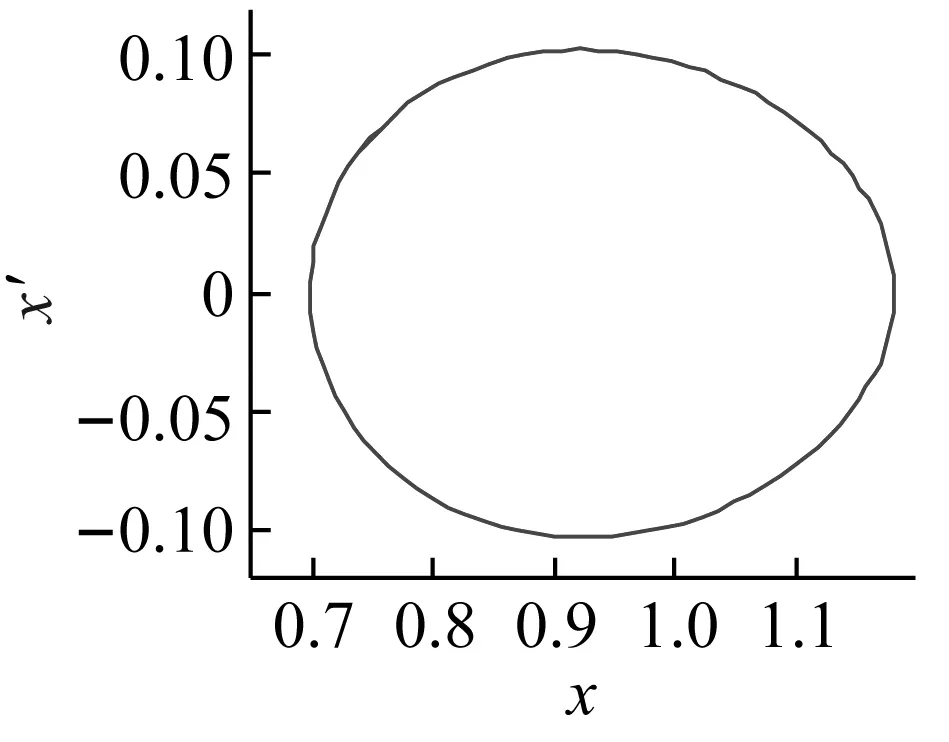
(b2)

(c2)图5 控制前后的时域响应和相平面Fig.5 The time response and phase plane before and after control
5 结 论
本文建立了含时滞反馈控制的直齿圆柱齿轮传动系统模型,应用多尺度法和数值计算方法对系统主共振的参激振动和时域特性进行了分析,主要可以得出:
(1)载荷波动和啮合刚度波动变化均会引起主共振的不稳定,与载荷波动不同,啮合刚度波动增加,主共振稳态振幅减小,但较小的啮合刚度波动也会导致系统的不稳定。
(2)位移、速度控制增益和时滞变化会引起系统主共振稳态幅值和峰值频率变化,增加位移增益,减小速度增益,而且取τd=T/4,τv=T/2时,能够使齿轮系统快速收敛到稳定解;
(3)一定的位移、速度增益和时滞会导致控制的不稳定,而且激励频率越高,控制参数触发系统不稳定的可能性越高,控制参数的不匹配可能加剧系统振动。
