基于SGA-BP-GA方法的FPSO舷侧结构耐撞性能优化设计

刘 刚，高明星，陈志颖，黄 一

(1.大连理工大学 船舶工程学院，辽宁 大连 116024；2.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024；3.中国船舶及海洋工程设计研究院，上海 200011)

FPSO (Floating Production Storage and Offloading)遭受守护船的撞击是其结构安全的主要威胁[1]。严重的碰撞将导致FPSO舷侧结构破裂，进而致使人员伤亡、经济损失及环境污染等事故的发生[2]。因此，为了提高FPSO舷侧结构的耐撞性能，开展FPSO舷侧结构的耐撞性能优化设计具有重要意义。

船舶碰撞优化的复杂性使得传统优化方法难以有效进行。碰撞优化的复杂性主要体现在以下两点：① 无法给出耐撞性目标函数与结构设计变量之间的显式方程；② 结构的碰撞响应主要依赖于非线性有限元计算，而大量样本点所需的计算成本非常高昂。针对难点一，目前主要通过在优化过程中引入试验设计和近似模型方法，进而根据有限样本点构造近似模型来逼近并替代结构耐撞性目标函数。广泛采用的近似模型法有Kriging法(KM)[3]、响应面法(RFM)[4-9]、径向基函数法(RBF)[10]、BP神经网络[11-14]等。其中BP网络由于其强大的非线性映射能力常用于结构耐撞性优化领域，但传统BP网络具有容易陷入局部极小值、对初始权值和阈值极其敏感等缺点，很难获得预测精度高且泛化能力强的网络响应面。为了解决传统BP网络的缺点，李慧等利用遗传算法(GA)对其进行优化，优化后的网络虽然预测精度有很大提高，但是其泛化能力仍不足于代替有限元计算，导致得到的最优结构设计失真。这主要是因为GA的局部空间搜索能力较弱，在优化BP网络时易出现早熟和陷于局部最优，使BP网络产生过拟合现象。为了增强GA的局部寻优能力，本文将模拟退火算法引入GA框架中[15]，形成模拟退火遗传算法(SGA)，并用于BP网络权重的组合优化中。针对难点二，本文使用Python语言编写参数化仿真计算程序[16]，可实现参数化建模、前处理、自动提交分析及自动后处理等功能，从而大大降低了计算成本。

本文基于正交试验设计和ABAQUS参数化仿真技术，结合BP神经网络、遗传算法和模拟退火算法，对传统的GA-BP-GA优化方法进行改进，提出一种新的结构耐撞性优化设计方法SGA-BP-GA，并以FPSO舷侧结构为研究对象，对其耐撞性能进行优化，可以快速获得最优的FPSO舷侧结构尺寸，以验证所提耐撞性优化方法的准确性与可行性。

1 耐撞性能优化设计方法——SGA-BP-GA

BP神经网络(BP Neural Network，BP)是一种利用误差反向传播算法对网络进行训练的多层前馈神经网络，由输入层、隐含层和输出层构成，具有较强的非线性映射能力。遗传算法(Genetic Algorithm，GA)是一种模拟生物界遗传与进化的并行随机搜索和全局优化算法，它通过选择、交叉、变异等操作对个体进行筛选，然后反复循环，直至获得最优个体(最优解)，具有较强的全局寻优能力。模拟退火算法(Simulated Annealing，SA)是一种模拟金属材料退火过程而建立的随机优化算法，在某一较高初温下，伴随温度参数的不断下降，结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即以时变概率跳出局部最优解并最终趋于全局最优，SA具有较强的局部搜索能力。

对于设计变量个数多的复杂结构耐撞性优化问题，仅采用单一算法(比如GA、SA等)对BP网络进行优化时，由于算法本身的缺陷，优化后BP网络的泛化能力仍不足以代替仿真计算。因此本文将退火算子引入遗传算法，形成全局寻优和局部搜索能力均较强的SGA，再结合正交设计、参数化仿真技术、BP网络、GA，提出一种适用于复杂结构的耐撞性优化方法SGA-BP-GA，其优化设计流程如图1所示。

SGA-BP-GA方法的基本步骤如下：

步骤1建立结构耐撞性优化数学模型，确定结构的优化参数；

步骤2利用正交试验确定合适的试验组，采用ABAQUS参数化仿真技术对其进行计算，进而得到BP网络的训练样本；

步骤3BP网络初始化，并利用SGA混合算法对其权值和阈值进行优化；

(1)初始化算法参数，将BP初始权重作为GA初始种群，并采用二进制对其进行编码；

(2)判断是否满足GA终止条件，若满足则输出BP最优权重，否则进行下一步；

(3)计算种群的适应度。本文将输出样本预测值与真实值之间的相对误差绝对值之和作为适应度函数Fit

(1)

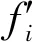
(4)对种群依次进行选择、交叉和变异操作，产生新种群。根据经验本文选三个遗传算子依次采用轮盘赌法、单点交叉和单点变异；

(5)对新种群中的最优个体进行模拟退火操作，具体过程如下。

① 将新种群中最优个体当做SA的当前解S1，并采用状态函数产生新解S2。本文采用的状态函数定义如下

S2=S1+β/20

(2)

其中β为区间[-0.5,0.5]内均匀分布的随机数。

② 采用相同的适应度函数Fit对S1和S2进行评价，并根据Metropolis法则判断是否接受新解S2，接受新解S2的概率P定义如下

(3)

③ 判断是否满足SA终止条件，若满足跳至步骤3中的第(2)步，若不满足则进行降温操作，然后循环步骤①～③，直至满足SA终止条件。本文选择线性降温函数，定义如下

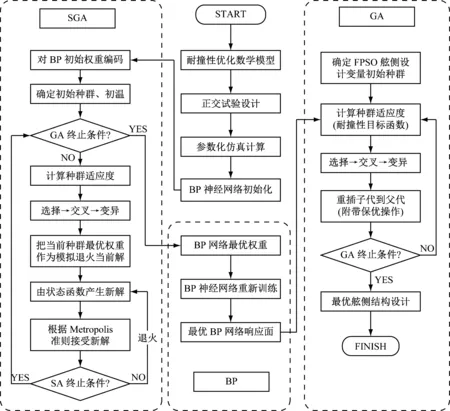
图1 GSA-BP-GA耐撞性能优化设计流程Fig.1 Crashworthiness optimization design flow of the GSA-BP-GA method

Tk+1=kt*Tk

(4)

式中，kt为降温速率，取0.9。

步骤4将最优权重赋给BP网络，并重新训练，获得近似最优BP网络响应面，进而替代有限元计算；

步骤5基于BP网络和GA开展舷侧结构的耐撞性能优化设计。

① 确定算法参数、初始化种群；

② 利用BP网络计算种群适应度，本文取耐撞性函数作为种群适应度函数；

③ 依次进行选择、交叉和变异操作，产生子代，然后将子代重新插入父代(保优)；

④ 判断是否满足GA终止条件，若满足则输出结构最优设计，否则循环步骤5中的第②步～第④步。

2 FPSO舷侧结构耐撞性能优化设计

2.1 模型描述

利用非线性有限元软件ABAQUS/Explicit，模拟2万吨级油船船首以3 m/s的速度正向撞击15万吨级FPSO舷侧结构的场景，其中撞击位置选为11 780 BL水线和16 030 BL水线间水平桁材与横向框架所限定的板架区域的中心位置。在保证计算精度的基础上，为了提高计算效率，本文将撞击船简化成半径为3m的半球形刚性球壳，且被撞FPSO只保留被撞区域的局部双舷侧结构。该局部双舷侧结构：长×宽×高=21.25 m×3 m×(4.25 m+4.25 m+5.1 m)，肋距为4.25 m，其原设计的横剖面图如图2所示。

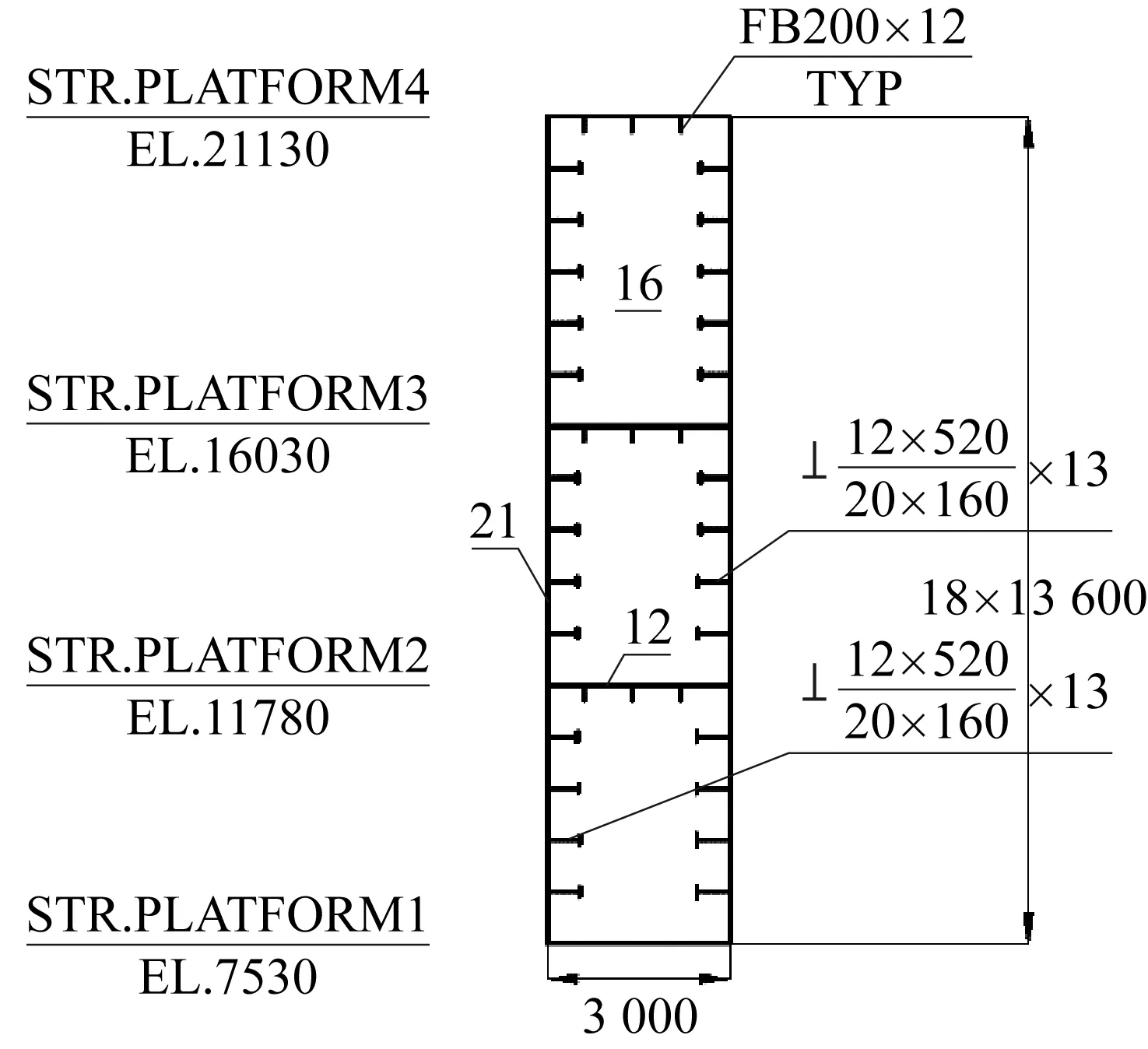
图2 FPSO局部舷侧结构横剖面图Fig.2 Cross-section of the FPSO partial side structure

仿真试验中，FPSO舷侧结构的材料为船用钢Q235，并且采用考虑应变率效应的Cowper-Symonds强化模型[17]。被撞局部双舷侧结构四周刚性固定，撞击船首仅保留X方向自由度，建立的有限元模型如图3所示。在基于数值仿真计算能够给出合理计算结果的前提下，对舷侧结构的碰撞仿真结果进行分析。图4为舷侧结构各构件的损伤变形云图，可知此时舷侧外板、外板纵骨、强肋板和平台发生较大的损伤变形，为主要的受力构件，因此本文选取外板板厚ts、T型纵骨腹板高度hw、T型纵骨腹板厚度tw、平台厚度tp和强肋板厚度tf五个参量进行优化。

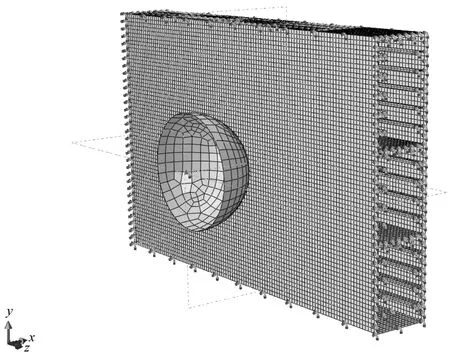
图3 碰撞有限元模型Fig.3 FEM of the FPSO side structure

2.2 耐撞性能优化数学模型与正交试验设计

本文主要对FPSO舷侧外板破裂前的耐撞性能进行优化设计。根据前期研究基础，被撞结构的比吸能和单位质量变形在一定程度上能够反映结构的耐撞性能，故本文综合考虑比吸能和单位质量变形，建立如下式所示的结构耐撞性能综合优化指标

F=αE·f(βE)+αC·f(1/βC)

(5)

式中：βE和βC分别为比吸能和单位质量变形；αE和αC分别为其隶属度权重系数，外板未破裂时取αE=αC=0.5；f()函数为指标的隶属度函数(无因次量)，隶属度计算方法如下式所示

(b)外板纵骨

(c)舷侧平台

(d)强肋板图4 FPSO舷侧结构各构件的变形云图Fig.4 Deformation contour of side structure’s components

(6)

将式(5)作为FPSO舷侧结构耐撞性能优化的目标函数，该值越大，就要求βE越大和βC越小，进而结构的耐撞性能就越好，可以充分体现结构耐撞性能的优劣。根据上一节确定的五个优化设计变量，建立如下的FPSO舷侧结构耐撞性优化数学模型

m≤194 000 kg

(7)

BP神经网络的预测精度和泛化能力与训练样本的质量和数量密切相关。利用正交试验设计确定的训练样本不仅具有典型性，又能保证一定数量，进而保证了BP神经网络的性能。本文对每个因素均取五个水平，即采用正交表L25(55)对FPSO舷侧结构各设计变量进行正交设计，共得到25组试验组，如表1所示。

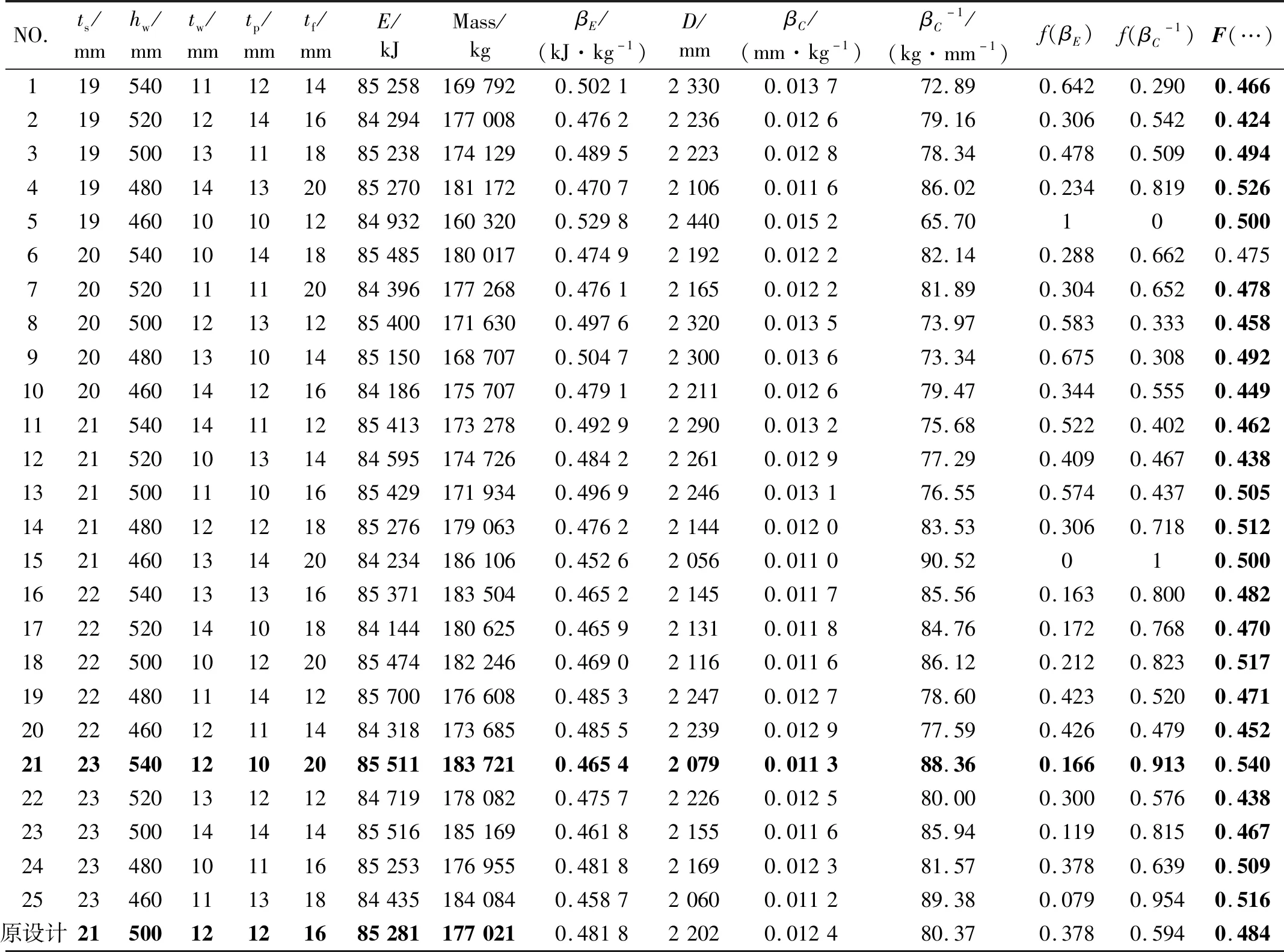
表1 正交试验设计结果Tab.1 Orthogonal experimental design results

2.3 ABAQUS参数化仿真计算

首先基于ABAQUS 脚本语言Python，编写以优化变量为形参的自定义函数sideStructure(…)，该函数可以实现参数化建模、其他前处理、自动提交分析及自动后处理的功能，其程序结构如图5所示。最后通过调用函数sideStructure(…)，以实现正交设计试验组的快速计算及结果提取，可大大减少计算成本。25组试验设计的计算结果及数据处理结果如表1所示。

2.4 四种BP网络训练样本预测结果对比

为了验证GSA-BP网络具有更高的预测精度和泛化能力，首先基于MATLAB语言分别编写以下四种FPSO耐撞性指标预测模型：传统BP网络预测模型、遗传算法优化BP网络预测模型(GA-BP)、模拟退火算法优化BP网络预测模型(SA-BP)及模拟退火遗传算法优化BP网络预测模型(SGA-BP)。然后分别利用四种BP网络对25组正交试验样本进行训练，其中以25组设计变量为输入样本，以25组比吸能和单位质量变形为输出样本。

图5 sideStructure(…)函数的程序结构Fig.5 Framework of the sideStructure(…)function

BP网络设计时，采用三层网络结构，其中输入层有5个神经元，隐含层有10个神经元，输出层有2个神经元；采用有动量的raingdm训练函数和learngdm学习函数，隐层神经元采用S型logsig传递函数，输出层神经元采用线性purelin传递函数，训练总步数为500步，均方差目标为10-4，学习速率为0.03。

设置遗传算法的参数时，初始种群规模为40，最大遗传代数为200；采用二进制编码，染色体长度为20；子代与父代之间代沟的概率为0.95，采用单点交叉，交叉概率为0.7，变异概率为0.01；以比吸能及单位重量变形的均方根误差(RMSE)作为种群的适应度函数，则适应度值越小，得到的权值和阈值越优；每代均基于适应度值对种群进行选择，从而将各代最优值遗传下去。

设置模拟退火算法参数时，初始温度为1 000，终止温度为10-3，各温度下的迭代次数为50，降温速率为0.9，以比吸能及单位重量变形的均方根误差(RMSE)作为解的状态评价函数，则状态函数值越小，得到的权值和阈值越优。

训练样本预测值与真实值相对误差的大小可以体现BP网络的训练精度。25组正交设计的四种BP预测相对误差曲线对比如图6所示，对应的相对误差范围如表2所示。由图6和表2可知：

(1)四种BP预测模型的预测精度由高到低依次为：SGA-BP、GA-BP、SA-BP和传统BP网络。其中，就25组输出样本预测而言，SGA-BP、GA-BP和SA-BP预测精度均在-3.5%～3%，可见经优化的BP网络性能远优于传统BP网络。

(2)传统BP网络的预测结果具有不稳定、高幅的特征，而SGA-BP、GA-BP和SA-BP网络的预测结果具有稳定、微幅的特征。

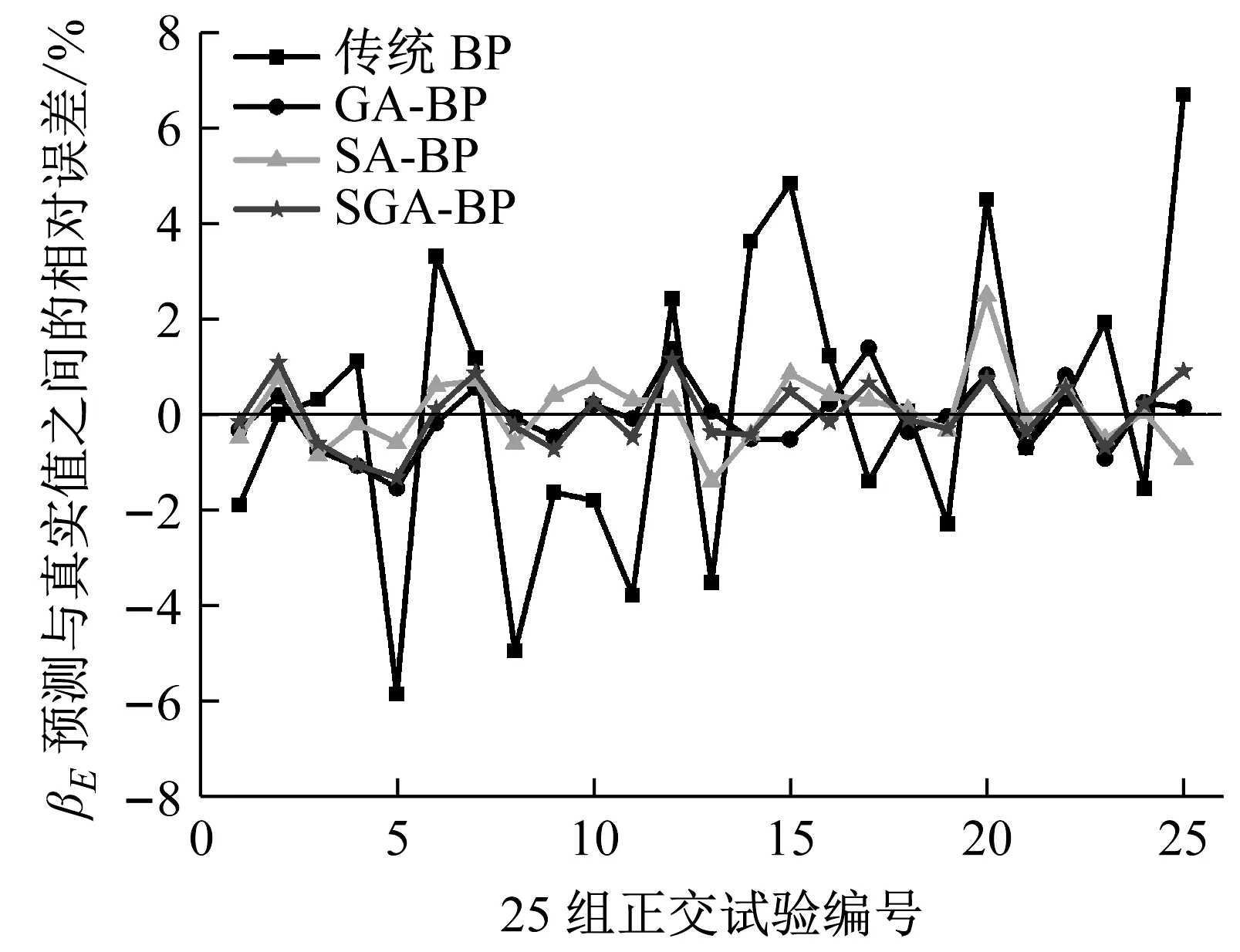
(a)比吸能

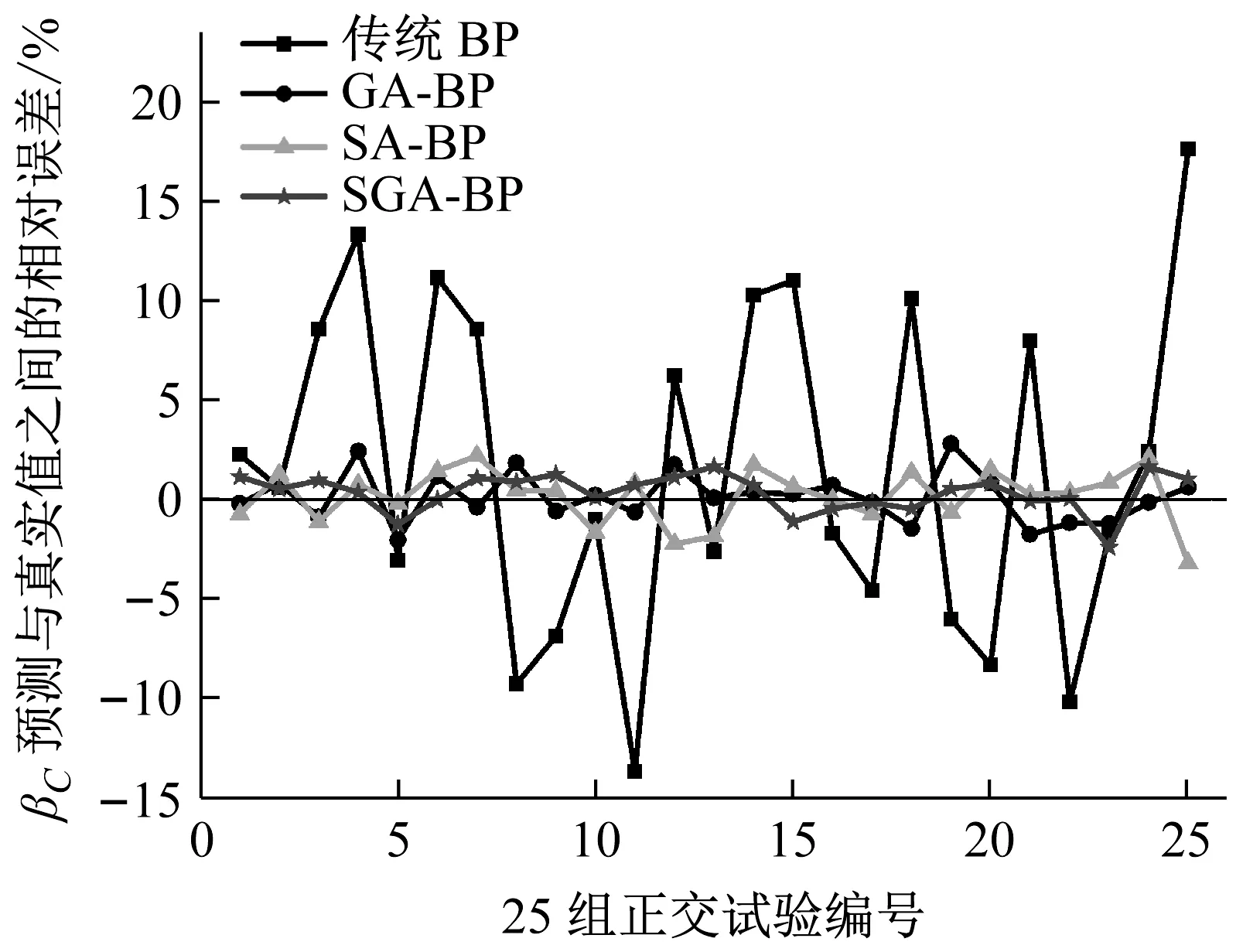
(b)单位质量变形图6 四种BP网络训练样本预测值与真实值相对误差对比Fig.6 Comparison of relative error between predicted values and true values of the training samples for the four BP networks

表2 四种BP网络预测值与真实值的相对误差范围Tab.2 Relative error ranges of predicted values and true values for the four BP networks

2.5 四种BP网络测试样本预测结果对比

泛化能力是指BP网络对未知样本的预测和推广能力，它是衡量BP网络优劣的最重要指标。本文随机选取12组非正交试验设计作为测试样本，以验证四种BP网络的泛化能力。采用ABAQUS参数化仿真技术对测试样本进行仿真计算，计算结果如表3所示。

四种BP网络测试样本的预测误差对比曲线如图7所示，对应的相对误差范围见表2。由图7和表2可知：

(1)四种BP预测模型的泛化能力由高到低依次为：SGA-BP、GA-BP、SA-BP和传统BP网络。

(2)GA-BP和SA-BP测试样本的预测误差均比训练样本的预测误差大，表明这两种BP网络均出现一定程度的过拟合现象，具有较差的泛化能力，其中以SA-BP网络更为严重。

(3)SGA-BP对测试样本和训练样本的预测误差相差无几，均维持在-3%～3%，表明经模拟退火遗传算法优化的BP网络兼有较强的训练精度和泛化能力，进而说明SGA-BP算法兼有遗传算法和模拟退火算法的优点。

表3 12组测试样本仿真计算结果Tab.3 12 sets of test sample simulation calculation results

(a)比吸能

(b)单位质量变形图7 测试样本预测值与真实值的相对误差对比Fig.7 Comparison of relative error between predicted values and true values of the test samples

图8为采用SGA算法优化BP网络权值和阈值时的进化曲线，可知曲线整体呈阶梯状不断下降，60代之前优化速率较高，主要利用了遗传算法的全局寻优能力；在60代～160代，优化效率明显降低，但BP网络仍不断趋于更优，主要是因为模拟退火算法的概率突跳特性可以跳出局部最优解，避免了优化进程产生早熟现象和陷于局部最优；遗传至160代时进化曲线趋于收敛，表明BP网络获得近似最优的权重。

图8 SGA优化BP权值和阈值的进化曲线Fig.8 Evolution process curve of BP optimized by SGA

通过上述的预测误差对比分析，发现SGA-BP网络在FPSO耐撞性指标的预测上优于其他三种网络模型，可以替代有限元计算和用于复杂的船体结构耐撞性优化问题。

2.6 SGA-BP-GA优化分析

以耐撞性目标函数作为遗传算法的适应度函数，分别利用SGA-BP-GA和GA-BP-GA方法对FPSO舷侧结构的耐撞性能进行优化，进一步验证SGA-BP-GA方法更加适用于复杂的耐撞性设计。

图9是两种方法优化FPSO舷侧结构耐撞性的进化过程曲线。结果表明，经过约40代的遗传，目标函数均已收敛，其中SGA-BP-GA对应的最大目标函数值为0.586，优于GA-BP-GA对应的0.579；SGA-BP-GA得到的最优结构设计为外板板厚ts=23 mm，T型纵骨腹板高度hw=472 mm，T型纵骨腹板厚度tw=14 mm，平台厚度tp=14 mm，强肋板厚度tf=20 mm，GA-BP-GA得到的最优设计为ts=20.4 mm，hw=460 mm，tw=12.5 mm，tp=10 mm，tf=20 mm。

图9 遗传算法进化过程曲线Fig.9 Evolution process curve of GA

表4为两种方法优化结果与原设计及正交试验最优设计的对比。结果表明，与原设计相比，SGA-BP-GA得到的耐撞性目标函数提高了21.7%，高于GA-BP-GA的19.6%和正交最优设计的11.6%；需要注意的是，SGA-BP-GA对应舷侧结构虽然耐撞性能最优，但结构质量也最大，这与采用的结构耐撞性评价体系有关，与具体的优化方法无关，同时也体现了本文采用的综合耐撞性指标需要进一步改进。

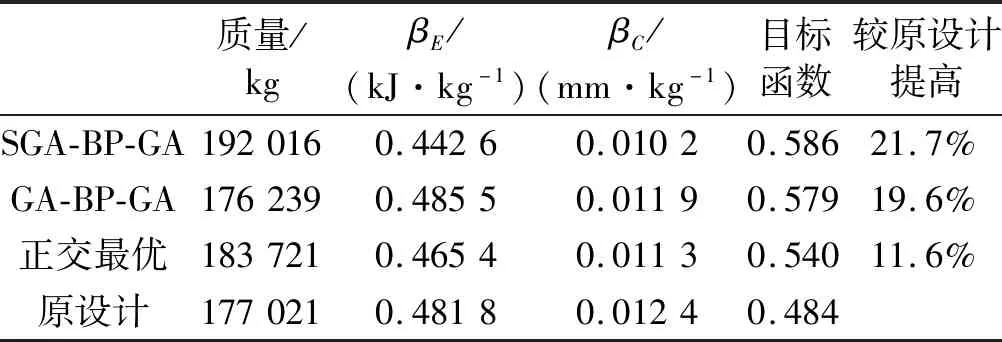
表4 两种方法优化结果与原设计、正交试验最优设计对比Tab.4 Comparison between the four optimization results

为验证SGA-BP-GA优化方法的准确性和可行性，本文对两种优化结果进行了仿真计算，结果如表5所示。由表可知，SGA-BP-GA最优设计的比吸能、单位质量变形及目标函数值与有限元计算值之间的相对误差绝对值均在1%之内，优于GA-BP-GA的3%，误差结果可以接受，这验证了SGA-BP-GA优化结果具有更高的准确度，同时也说明了经SGA混合算法优化的BP神经网络具有更好的预测精度和泛化能力；SGA-BP-GA最优设计的目标函数仿真值为0.592，比原设计提高了22.3%，比GA-BP-GA最优设计提高了5.34%，说明SGA-BP-GA优化方法具有更高的可行性，能较好的适应于复杂的船舶结构耐撞性优化设计。

表5 SGA-BP-GA优化结果与有限元计算值比较Tab.5 Comparison between SGA-BP-GA optimization results and finite element calculations

3 结 论

(1)采用SGA混合算法对BP网络进行了优化，解决了单一算法优化BP网络易出现早熟现象或陷于局部最优的缺点，并以FPSO舷侧结构优化为例，验证了SGA-BP网络比传统BP、SA-BP及GA-BP具有更高的预测精度和泛化能力。

(2)提出并搭建了一种新的结构耐撞性优化方法SGA-BP-GA，并以FPSO舷侧结构优化为例，验证了SGA-BP-GA方法比GA-BP-GA具有更高的准确性和可行性，能够更好的应用于复杂的船舶结构耐撞性优化设计，其中基于仿真计算结果合理的前提下，SGA-BP-GA最优设计较原设计耐撞性能提高了22.3%，较GA-BP-GA最优设计提高了5.34%。

(3)基于Python语言编写了参数化仿真计算程序，可实现参数化建模、前处理、自动提交分析及自动后处理的功能，从而大大降低了计算成本。

(4)所提优化方法SGA-BP-GA具有通用性，也可为比如结构抗爆性优化等复杂优化问题提供参考，具有较好的工程应用前景。