CRTS Ⅰ型双块式无砟轨道轨枕连接面损伤行为分析及识别研究

任娟娟，韦臻，曾学勤，杜威，田晋成，刘伟

（1. 西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都 610031；2. 西南交通大学 土木工程学院，四川 成都 610031）

1 概述

双块式无砟轨道是我国高速铁路无砟轨道结构的主要类型之一，具有结构形式统一、建造成本较低等优点。截至2018 年底，已建成的高速铁路无砟轨道线路共44 条，其中,西成高铁、武广高铁及贵广高铁等27 条线路都采用了CRTS Ⅰ型双块式无砟轨道。CRTS Ⅰ型双块式无砟轨道作为行车基础，长期暴露在复杂的自然环境中，受列车荷载、温度、雨水等因素的长期作用，轨道结构易出现损伤，影响轨道的整体强度。现场调研中发现，双块式无砟轨道容易出现轨枕松动、新旧混凝土接触面的裂缝、轨枕渗浆等问题（见图1）。经现场调查和资料分析，轨枕松动主要是由施工不当、列车荷载及环境等作用造成的。在施工过程中，养护不当将会减小道床板与轨枕块层间咬合力，从而降低层间界面强度，产生层间损伤[1]；在列车荷载的长期作用下，轨枕与道床板接触部分产生微小裂纹，加之雨水的渗入，裂纹不断扩展导致轨枕松动和离缝冒浆等现象的出现，当损伤情况较为严重时，会造成行车轨枕空吊，最终影响行车平稳性和安全性。

图1 双块式无砟轨道轨枕连接面问题

针对双块式无砟轨道损伤，胡佳等[2]研究了整体升温、整体降温对道床板受力、受损区域和损伤扩展规律的影响。在轨枕松动病害对车辆、轨道系统的动力性能影响方面，杨荣山等[3]通过建立含轨枕松动病害的车辆-双块式无砟轨道-下部基础垂向耦合振动模型，研究列车速度、轨枕空吊高度及轨枕松动数量对轨道结构动力响应；和振兴等[4]建立考虑单侧轨枕空吊的车辆-轨道空间耦合振动模型，分析城市轨道交通弹性短轨枕轨道中轨枕空吊对车辆、轨道系统的振动响应影响。针对无砟轨道层间界面位置损伤识别，赵佳[5]通过设置不同程度的无砟轨道层间损伤，利用模态分析方法得到不同工况下的振型模态、模态曲率以及应变模态数据，对比分析获取模态参数对层间损伤的敏感性规律，确定损伤位置及范围；武思思[6]通过对冲击荷载下轨道板的振动响应变化规律分析，从奇异值、信息熵等多角度提取了损伤特征指标进行脱空识别，有效地进行了层间脱空检测；胡琴等[7]提出的基于BP 神经网络对板式无砟轨道层间损伤位置进行识别，以参数化处理的振型作为BP 神经网络的输入对各损伤工况下板式轨道CA 充填层损伤位置进行识别发现。

上述文献在对损伤行为进行分析时，鲜有考虑双块式无砟轨道轨枕块和道床板连接面（简称轨枕连接面）位置脱粘损伤识别，且层间损伤检测方法较为繁琐，不能快速有效地检测出实际的损伤程度。基于以上不足，采用内聚力模型，建立基于轨枕连接面损伤的有限元计算模型，提取道床板和轨枕块在列车荷载下的振动响应，基于小波包分解理论分析振动信号在各频带的能量变化规律提取损伤特征指标，获取轨道结构的损伤状态[8-9]。

2 双块式无砟轨道损伤动力学模型

因施工缺陷和温度荷载等原因，无砟轨道轨枕连接面易发生脱粘损伤，相关联的结构部件也会出现异常的振动响应。因此通过研究振动响应对轨枕连接面损伤行为进行分析。

2.1 层间内聚力模型

在处理新老混凝土界面时，将其考虑为一个单独部分，使用内聚力模型，采用双线性张力-位移曲线来描述层间本构关系[10]。新旧混凝土的三区粘结模型见图2。在定义内聚力模型的力学性能时，需确定内聚力模型的相关参数：刚度、极限强度以及临界断裂能。对于内聚力单元的厚度，在建模时考虑其为单位厚度，由K=E/L可知（K为刚度；E为弹性模量；L为单元厚度），此时界面刚度与弹性模量数值相同，因此界面的张力-位移曲线可考虑为应力-应变关系曲线（见图3）。

在对轨枕连接面损伤行为分析时，内聚力单元参数见表1。

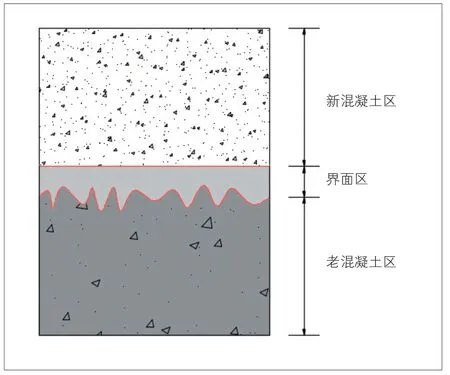
图2 新旧混凝土的三区粘结模型

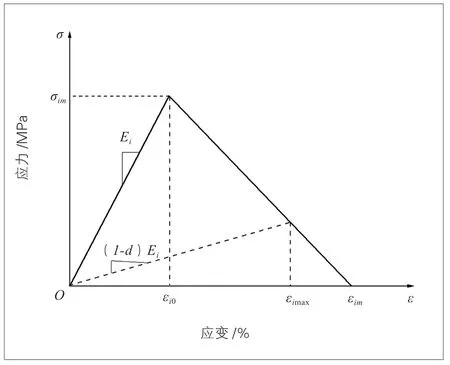
图3 层间界面应力-应变关系曲线

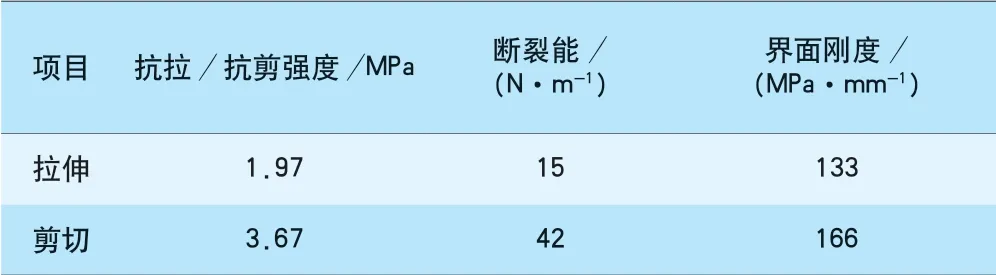
表1 内聚力单元参数

2.2 计算模型

模型采用动力隐式算法分析轨枕连接面损伤状态对轨道结构动力响应的影响。为能准确分析轨枕连接面位置处的损伤行为，同时保证较高的计算效率，以下只对3 跨扣件的轨枕连接面进行损伤考虑，其余部分均采用线弹性模型。内聚力单元失效后，连接内聚力单元的两边面通过接触相互作用来模拟抗压和抗剪等行为[10]。CRTS Ⅰ型双块式无砟轨道结构尺寸及参数分别见表2。建立的CRTS Ⅰ型双块式无砟轨道空间损伤有限元分析模型见图4。

表2 CRTS Ⅰ型双块式无砟轨道结构主要参数

图4 CRTSⅠ型双块式无砟轨道空间损伤有限元分析模型

2.3 列车动荷载激励

对于列车动荷载，基于Ansys/Simpack 联合仿真建立的车辆-轨道耦合动力学模型，获取扣件位置钢轨支点压力时程曲线作为激励。根据遂渝线现场调研情况，选用CRH2 动车组（见图5）[11]，为模拟现场线路状况，在动力学模型中采用中国高速铁路无砟轨道高低不平顺谱。

图5 CRH2 动车组车厢构造图

利用车辆-轨道耦合动力学模型，可计算得到车速为200 km/h 运行状态下某个车轮与钢轨间相互作用力时程曲线（见图6），再根据高斯型钢轨支点压力时程表达式[12]，即可得到某一扣件位置处钢轨支点压力时程曲线[13]：

图6 车轮与钢轨间相互作用力时程曲线

式中：Qi为车轮与钢轨间相互作用力；ψi为扣件荷载分担比；v为列车运行速度；ΔIi为列车第i个车轮与第1 个车轮的间距；n为列车车轮数量；yo、A、ω均为拟合参数。

将4 个车轮（图5）的作用效应叠加[14]，最终获得1 节CRH2 客车车厢通过某扣件时，该扣件位置的钢轨支点压力时程曲线（见图7）。

模拟数据与遂渝线Tekscan 实测钢轨支点压力时程曲线数据相近[15]，验证了模拟数据可靠性。

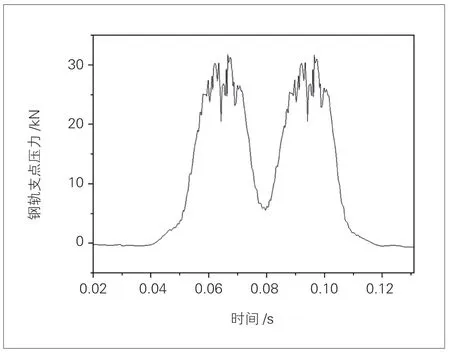
图7 扣件位置钢轨支点压力时程曲线

2.4 工况设置及测点布置

通过现场调研发现双块式无砟轨道轨枕连接面普遍存在脱粘现象。文献[16]分析认为在整体降温作用下，道床板与轨枕连接面长边易产生脱粘，并沿道床板深度方向延伸；在整体升温作用下，道床板与轨枕连接面底边首先产生脱粘，随升温幅度的增加，损伤范围逐渐增加。为实现轨枕连接面脱粘损伤程度识别，分别在轨枕连接面长边和底面设置不同程度的脱粘损伤，通过采集轨枕块和道床板在外荷载激励下的振动响应，提取损伤信息，确定损伤特征指标。

（1）损伤工况设置。设置脱粘程度为无脱粘、25%脱粘、50%脱粘、75%脱粘、100%脱粘5 种，不同脱粘工况见图8（阴影区域为脱粘区）。

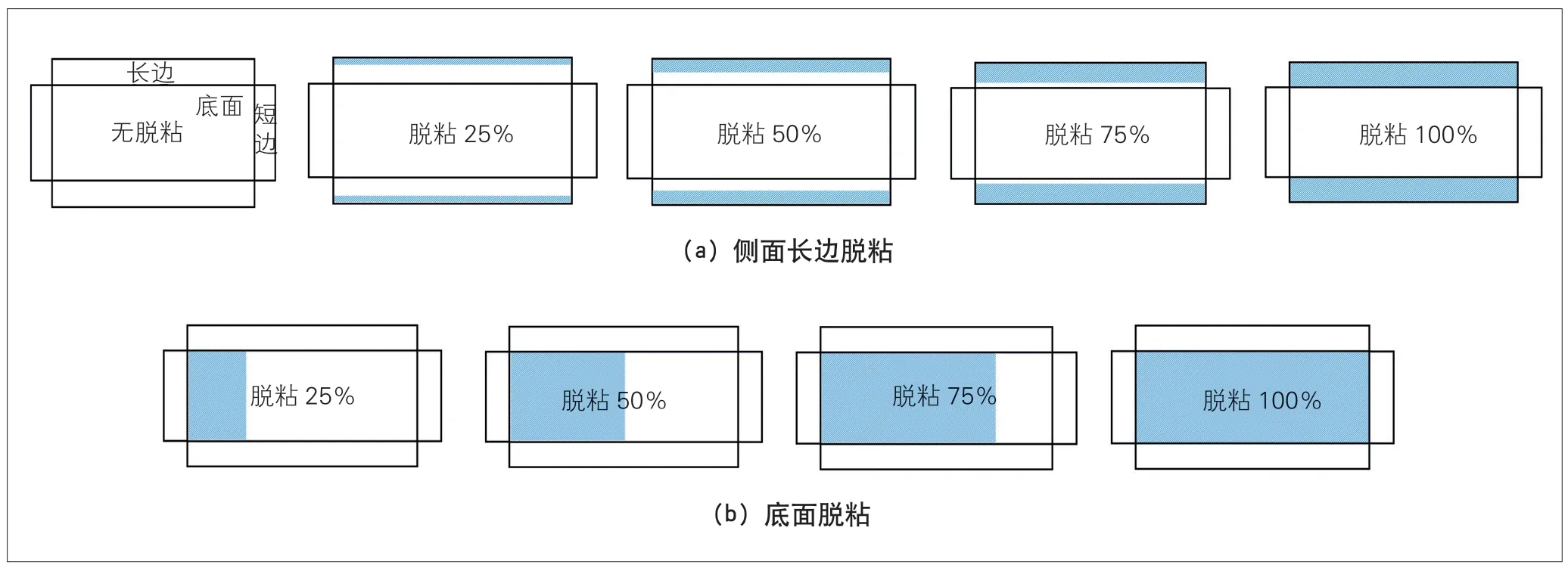
图8 脱粘工况示意图

（2）测点布置。取轨枕块中心及其道床板对应位置为检测位置（见图9）。

轨道动力学模型对0.020～0.131 s 区段内的采样数据进行分析，采样频率取1 000 Hz。传感器采集的信号数据分为应变类和位移类，但在实际工程应用中，加速度信号是位移类测试数据中比较容易获取且对损伤最为敏感的检测指标，因此提取列车荷载作用下检测点的加速度时程数据进行分析与研究。

图9 检测点示意图

3 轨枕连接面损伤行为分析

3.1 侧面长边脱粘损伤工况

提取长边不同损伤程度工况下，各检测点的加速度时程数据。通过对比各检测点在不同损伤程度下的加速度时域曲线，图像之间的差别不大，不能直观反映损伤的特征。因此，引入小波包分解理论，基于信号处理和数据分析的手段发掘振动信号内部隐含的规律性损伤信息，即特征指标的提取。当结构出现损伤时，结构自身振动响应特性将会出现变化，损伤对于各频带的影响是不同的，有些频带加强，有些频带减弱，最终导致各频带的频率或能量与正常状态相比出现差异。不同损伤状态下各频带包含的能量信息不同，因此，可以通过对比不同损伤情况下各频带能量信息的差异达到识别损伤程度的目的。小波包分解能自适应地依据分析要求和信号本身的特性选取相应的频带信息与信号的幅值谱进行匹配，准确地提取出振动信号各频带的信息[17-19]。

3.1.1 轨枕块

利用小波包分解理论分别对3 个检测点的加速度时域数据进行“db4”三层小波包分解，并分别提取检测点各频率分段的能量以及各检测点信号的总能量。轨枕块检测点不同脱粘程度下各频带所对应的能量见表3。

由不同脱粘程度下检测点各频带的能量可得，各频率分段的能量均随损伤程度的增加出现一定变化，但呈明显变化规律的是438～500 Hz 频带，轨枕块上检测点时频域范围内在此频带的能量随脱空损伤程度的增加而严格增大，其能量随损伤程度的变化曲线见图10。因此，可将轨道板上检测点时频域范围内438～500 Hz 频带的能量作为损伤特征指标。

表3 轨枕块侧面不同脱粘损伤程度下各频带对应能量 J

图10 轨枕块438 ～500 Hz 频带侧面损伤对应能量

3.1.2 道床板

道床板检测点不同脱粘损伤程度下各频带所对应的能量见表4。由不同脱粘损伤程度下道床板检测点各频率分段的能量可得，各频率分段的能量均随损伤程度的增加出现一定的变化，但呈明显变化规律的是0～63 Hz、188～250 Hz、250～313 Hz 这3 个 频 带， 这3 个频带的能量随脱空损伤程度的增加而严格增大，其能量随损伤程度的变化曲线见图11。因此，可将轨道板上检测点时频域范围内0～63 Hz、188～250 Hz、250～313 Hz 这3 个频带的能量作为损伤特征指标。

表4 道床板侧面不同脱粘损伤程度下各频带对应能量 J

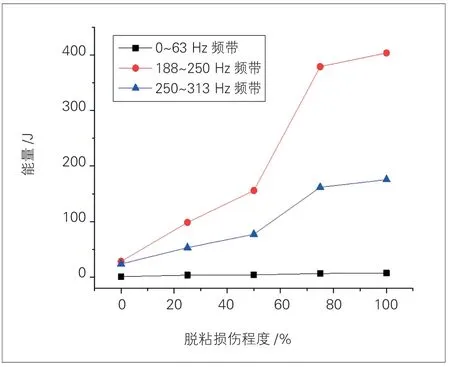
图11 道床板各频带侧面损伤对应能量

3.1.3 总能量

轨枕块和道床板检测点各频率分段的能量已经获得，对其数值进行求和即可获得各检测点振动响应信号的总能量，其随脱粘损伤程度的变化见表5。

不同脱粘损伤工况下各检测点的小波包分解总能量变化趋势见图12。

由图12 可得，总能量随脱粘程度的增加也呈现出增大的趋势，说明随侧面脱粘损伤程度的增加，在列车荷载的冲击作用下，轨枕块和道床板的振动响应强度和幅度逐渐变大。

表5 各检测点长边脱粘下损伤程度对应总能量 kJ

图12 侧面损伤程度对应总能量

3.2 底面脱粘损伤工况

3.2.1 轨枕块

轨枕块检测点在轨枕连接面底面不同脱粘损伤程度下各频带所对应的能量见表6。

表6 轨枕块底面不同脱粘损伤程度下各频带对应能量 J

由不同脱粘损伤程度下轨枕块检测点各频率分段的能量可得，各频率分段的能量均随损伤程度的增加出现一定变化，但呈明显变化规律的是63 ～125 Hz、250 ～313 Hz、313 ～375 Hz 这3 个频带，这3 个频带的能量随脱空损伤程度的增加而严格增大，其能量随损伤程度的变化曲线见图13。因此，可将轨道板上检测点时频域范围内63 ～125 Hz、250 ～313 Hz、313 ～375 Hz 这3 个频带的能量作为损伤特征指标。

图13 轨枕块各频带底面损伤程度对应能量

3.2.2 道床板

道床板检测点在轨枕连接面底面不同脱粘损伤程度下各频带所对应的能量见表7。

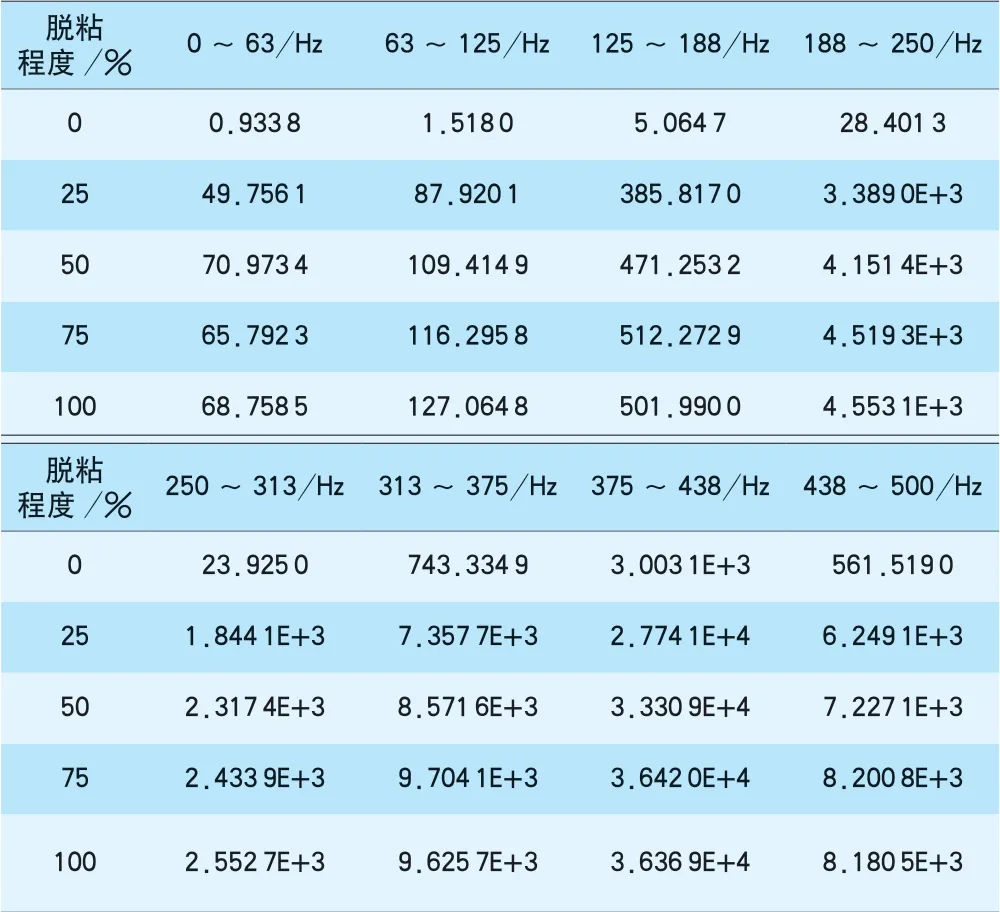
表7 道床板底面不同脱粘损伤程度下各频带对应能量 J

由不同脱粘损伤程度下道床板检测点各频率分段的能量可得，各频率分段能量均随损伤程度的增加发生变化，但呈明显变化规律的是63 ～125 Hz、188 ～250 Hz、250 ～313 Hz 这3 个频带，其能量随损伤程度的变化曲线见图14。

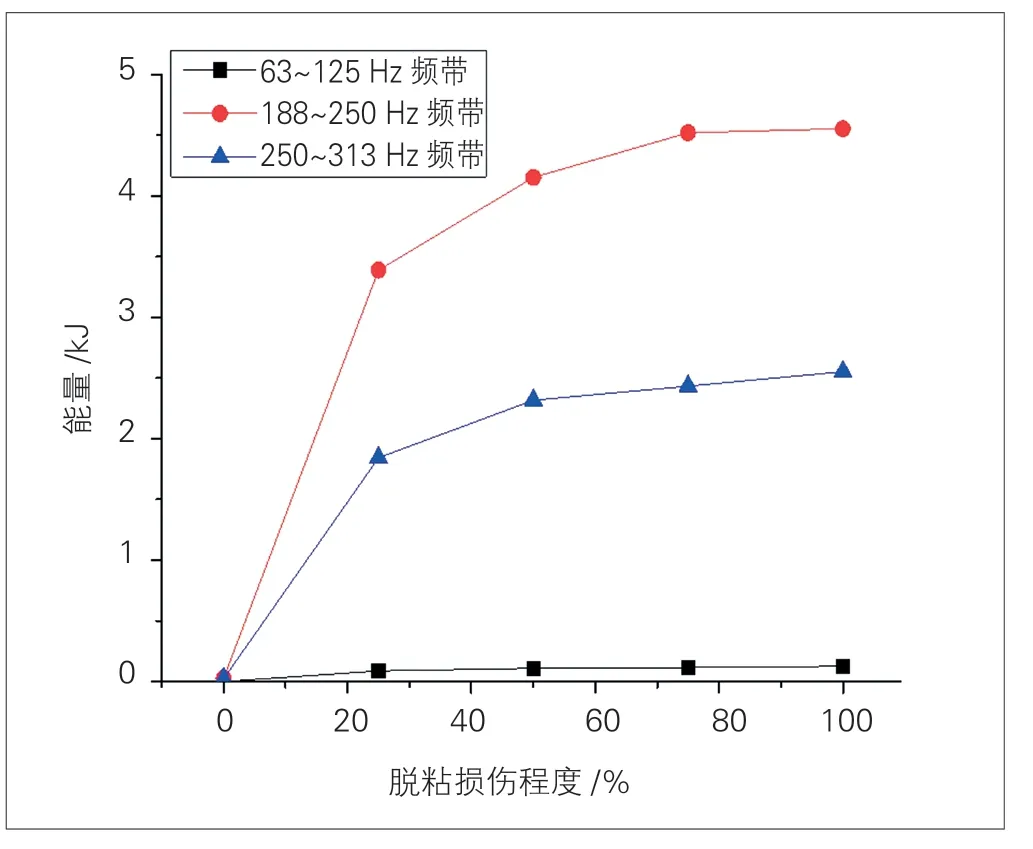
图14 道床板各频带底面损伤程度对应能量

3.2.3 总能量

道床板上检测点时频域范围内63～125 Hz、188～250 Hz、250～313 Hz 这3 个频带的能量随脱空损伤程度的增加而严格增大，因此，可将道床板上检测点时频域范围内这3 个频带的能量作为损伤特征指标。轨枕块和道床板检测点各频率分段的能量已经获得，对其数值进行求和即可获得各检测点振动响应信号的总能量，其随脱粘损伤程度的变化见表8。

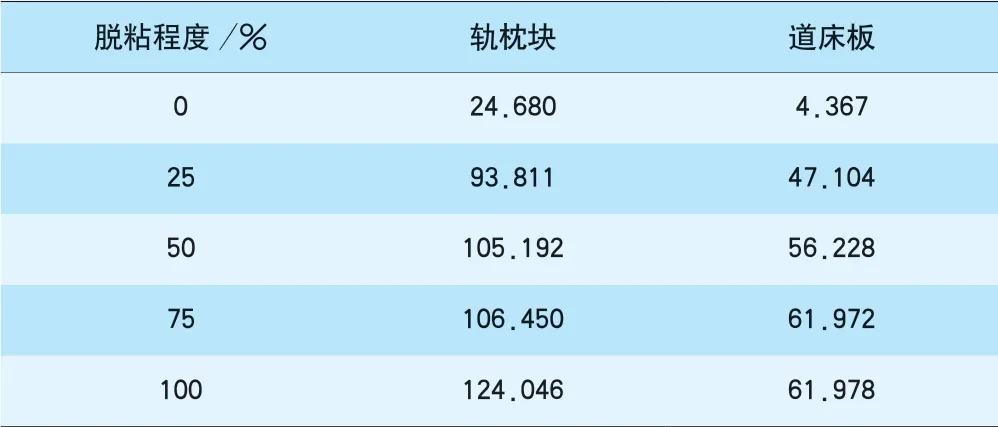
表8 各检测点底面脱粘损伤程度对应总能量 kJ

不同脱粘损伤程度下各检测点的小波包分解总能量变化趋势见图15。总能量随脱空程度的增加也呈现出增大的趋势，说明随底部脱粘损伤程度的增加，在列车荷载的冲击作用下，轨枕块和道床板的振动响应强度和幅度逐渐变大。

图15 底面脱粘损伤程度对应总能量

4 结论

基于小波包分解对轨枕面脱粘损伤下CRTS I 型双块式无砟轨道振动响应进行分析，得出如下主要结论：

（1）双块式无砟轨道轨枕连接面脱粘将显著提升轨枕块和道床板的振动响应，轨枕连接面底部脱粘对振动响应的提升更为剧烈。

（2）在外部荷载作用下，双块式无砟轨道轨枕连接面脱粘时的自身振动响应发生较大变化，通过小波包分解提取频带能量作为损伤特征指标，其频带能量增幅达到6%以上，可以识别损伤的程度。

（3）计算结果显示轨枕块频带总能量大致为道床板的2 倍，表明随着轨枕连接面脱粘损坏程度的加深，轨枕块振动响应显著提升，向下传递致使道床板振动响应提升。因此，在CRTS I 双块式无砟轨道运营过程中应严格控制轨枕连接面脱粘程度。