基于声波的快速温度场重建系统研究

代伟嵩，周新志，白兴都，张若彬

（四川大学 智能控制研究所，四川 成都 610041）

0 引 言

温度是描述物质状态的重要参数之一，它的测量与控制在工业生产中占有举足轻重的地位。声学测温方法是一种非接触测温方法，与传统接触式测温方法比，具有测温范围广、非接触式传感、成本低廉等优点，可用于海洋热液、电站锅炉、仓储粮食等温度场的测量[1-3]。

使用声学法测温时，快速准确地获取声波飞渡时间至关重要[4]。颜华等研制了一套基于数据采集卡的声波时延测量系统，通过互相关算法得到了相对稳定的时延数据[5]。张天恒等提出一种以高精度A/D 和高速FPGA为硬件核心的时间测量系统，使用细分插补法在真空管测得了精确的飞渡时间[6]。熊庆宇等设计基于FPGA+DSP 的测量系统，采用回波峰值法得到了精确的单路时间数据[7]。

目前的研究虽然也取得了一些成果，但在确定飞渡时间时，往往需要设计复杂的算法对回波进行处理，拖慢了系统的运算速度。为了更为快速精确获取的声波飞渡时间，本文设计了一种以超声波模拟前端TDC1000为核心的测温系统，该芯片可直接获取高信噪比的回波信号，通过设定合适的阈值电压，即可得到准确的飞渡时间。并针对经典最小二乘法重建温度场图像缺失问题，提出基于Reflected Sigmoid 函数的重建算法[8]。实验验证，该系统一次运行时间在200 ms 左右，结合本文重建算法，能够较为快速准确地重建出被测区域温度场图像，满足设计要求。

1 声学测温原理及重建算法

1.1 声学测温基本原理

声学测温原理是基于声波在同一介质中传播速度随温度改变这一特性，从而间接地推导出介质温度[9]。气体介质中，声速与介质和温度间的函数关系式为：

式中，Z为气体常数，在空气中，Z=20.05。在已知被测区域尺寸时，可推导出温度测量结果：

式中：T为温度；L为被测区域尺寸；t为飞渡时间。由于L，Z已知，因此只要得到飞渡时间t便可求得相应的温度[10]。

1.2 基于Reflected Sigmoid函数的重建算法

最小二乘法可以快速计算出各子温区中心点的温度，通过插值方法得到子温区中心点之外的温度。但由于算法固有缺陷，无法得到最外侧子温区中心点到区域边界的温度，当划分子温区数目较少时，温度缺失非常严重。针对该问题，本文使用Reflected Sigmoid 函数对最小二乘法的结果进行插值。Reflected Sigmoid 函数是一种典型的径向基函数，具有良好的泛函逼近能力。这样可在保留最小二乘算法快速、简便、鲁棒性强的优点下，重建出完整的温度场分布。

本算法是一种两阶段重建算法。第一阶段将被测区域划分为N个子温区，通过最小二乘法求出各子温区平均温度，并将此温度值作为子区域几何中心点温度值，即T=[t1t2…tN]T。第二阶段，使用N个 Reflected Sigmoid 函数的线性组合来重建出温度T（x，y），即：

式中，T（x，y）为被测区域温度函数，即 Reflected Sigmoid函数，以此为中心点，其在二维平面的表达式为：

式中，a为形状参数，可通过仿真实验得到。

由最小二乘法，已得到子温区几何中心点温度矩阵T，设子温区中心点为(xk,yk)，则：

改写为矩阵形式：

式中：E=[ε1ε2…εN]T为待求的N个 Reflected Sigmoid函数的系数矩阵；Φ为Reflected Sigmoid 函数子温区几何中心的函数值矩阵，其形式为：

当超声波探头和子温区确定后，矩阵便可以确定，由此可解出矩阵E=[ε1ε2…εN]T，将矩阵E代入式（6）便可求得待测区域完整温度场T（x，y）。

2 测温系统设计

测温系统的结构如图1所示。系统采用STM32 作为控制芯片，以超声波模拟前端TDC1000 为核心，配合外围电路完成超声波收发模块的选通、升压、接收、滤波等功能。使用TDC7200 为时间测量芯片，实现飞渡时间测量。主控芯片与TDC1000 和TDC7200 间通过SPI总线通信，以实现对TDC7200 发送控制指令、读取测量数据，最后通过RS 232 总线将数据传输到上位机，对温度场进行重建。

图1 系统结构图Fig.1 Structure diagram of system

2.1 超声波收发电路

为了更好地驱动超声波换能器并准确接收到回波，本系统选用TDC1000 取代传统的超声波模拟电路。该芯片可根据实际需要，可输出频率在31.25 kHz～4 MHz的超声波驱动信号，并自带LNA 和PGA 两级放大功能，结合外围电路即可完成基本的选频滤波和放大功能，简化了硬件设计难度。面对不同路径回波信号强度不同问题，可通过SPI 接口动态设置相应的的阈值，使得飞渡时间测量更为高效、简洁。

TDC1000 的工作时序如图2所示。TDC1000 收到TRIGG 信号后，立刻发送超声波驱动信号TX 至换能器，同时向 TDC7200 发 START 信号，TDC7200 开始计时。超声波信号发送一段时间后，TDC1000 会在COMMON模式下拉高接收端管脚电位，提供直流偏置，以消除探头余振，并开启自动调零功能，抑制干扰信号。随后芯片进入接收侦听模式，等待接收回波信号。接收到的原始信号将被做放大、滤波处理，一旦信号幅值达到阈值，便发送一个STOP 信号至TDC7200，完成一次测量。

图2 TDC1000 工作时序图Fig.2 Working time sequence of TDC1000 system

声学测温中，换能器性能关系到回波的强度、波形及灵敏度。本系统选用NU40C16TR-1 型压电超声波换能器，工作频率为40 kHz，最低灵敏度为-66 dB。由于TDC1000 驱动信号幅值仅为5 V，若用其直接驱动换能器，会导致回波信号精度不高。因此，需使用TPS61170芯片将驱动信号升压至30 V，再用其驱动换能器。

2.2 时间测量电路

TDC7200 是一种分辨率达到ps 级的时间数字转换器，可自动补偿时间与温度偏差。芯片可测量START信号和最多5 个STOP 信号的时间间隔。当与TDC1000配套使用时，可直接获取精确的飞渡时间，无需使用单片机定时器来手动计时，降低了程序的编写难度，提高了系统运行速度。原理图见图3。

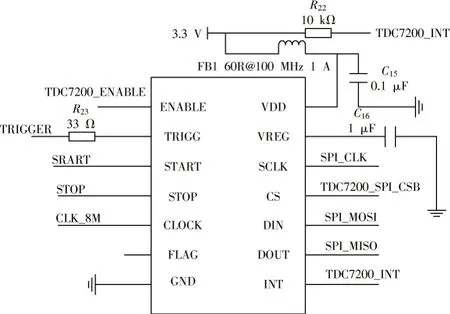
图3 TDC7200 电路原理图Fig.3 Circuit schematic diagram of TDC7200

2.3 软件设计

系统的软件设计包括用C 语言编写的嵌入式程序和用Matlab 编写的上位机程序，主要实现STM32 对外围芯片的控制和温度分布图像的重建。流程图见图4。

在系统上电启动后，STM32 控制TDC1000 发激励脉冲信号给超声波换能器，并控制另一换能器处于接收模式，此时TDC7200 开始计时。当收到回波信号后，给TDC7200 发截止信号，完成一次计时。当所有路径测量完成后，通过RS 232 总线将数据发送至上位机，完成图像重建。

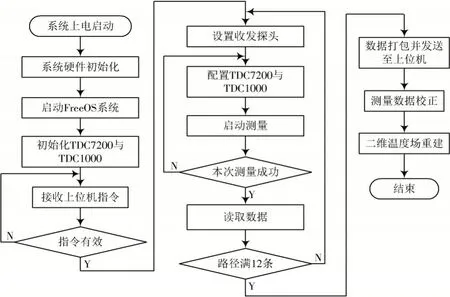
图4 系统流程图Fig.4 Workflow chart of system

3 实验验证及分析

为了验证本文设计的超声波测温系统硬件及图像重建算法的准确性，在实验室中搭建了实验平台，进行了声学法温度场重建实验。实验平台与声波传播路径如图5所示。

图5 实验平台与声波传播路径Fig.5 Experiment platform and acoustic wave propagation path

实验将一个功率为1 kW 的电热炉放置在1.2 m×1.2 m 的正方形区域中心，8 个超声波换能器采用对称布局固定在实验平台上，形成12 条传播路径，其中电炉距离测量截面约15 cm，待电炉炉温稳定后开始测量。考虑到实验条件限制，仅设计了室温无加热，单峰对称加热2 种情况。表1给出了加热前各路径传播时间及变化，可以看出，温度上升后各路径飞行时间均有减少，其中经过热源的路径减少明显。

表1 加热前后飞渡时间Table 1 Flight time of different paths before and after heating

获取飞渡时间数据后，分别使用最小二乘法和RS函数插值法重建出温度场图像。其中，室温无加热形状参数a为0.305，单峰加热时形状参数a为0.225。图6、图7为温度场重建图像。由重建图像可知最小二乘法图像边缘严重缺失，与之相比RS 函数插值方法能够重建出完整的温度场，虽相比最小二乘出现了些许畸变，但总体仍能反应出热源位置及温度分布趋势。

图6 室温无加热重建结果Fig.6 Reconstruction results without heating at room temperature

图7 单峰对称加热重建结果Fig.7 Temperature field reconstruction images with symmetrical heating of single peak

为了进一步验证重建图像的准确性，本实验选取若干被测区域的典型位置作为采样点，使用DS18B20 对采样点进行测温，将测得温度作为实际温度与重建温度作为对照。图8、图9给出了相应的结果与偏差。对上述结果做误差分析，得到实验误差表2、表3。表中给出了最大绝对误差、平均绝对误差和均方根误差。可以看出，室温无加热时两者重建效果接近，但是单峰对称加热时RS 函数插值精度明显提高。

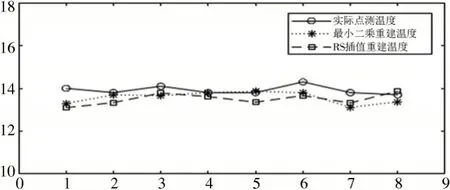
图8 室温无加热测量结果Fig.8 Measured results without heating at room temperature

图9 单峰对称加热测量结果Fig.9 Measured results with symmetrical heating of single peak

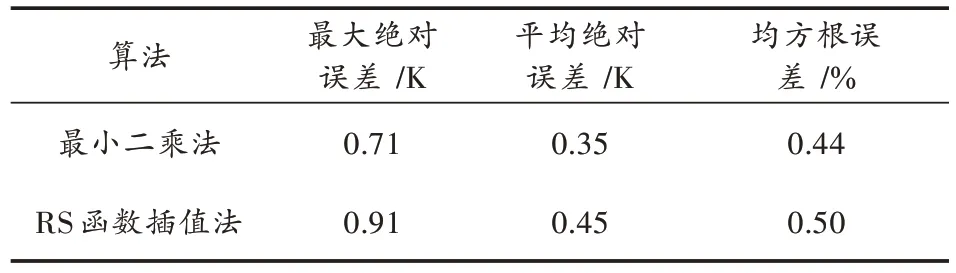
表2 室温无加热重建误差表Table 2 Reconstruction error without heating at room temperature

表3 单峰对称加热重建误差表Table 3 Reconstruction error with symmetrical heating of single peak

4 结 语

本文以声学测温原理为基础，设计了一种以TDC1000 为核心的声学测温系统。该系统相比基于传统的声学测量系统，可由外围芯片直接获取飞渡时间，避免了设计复杂算法来分析回波波形，提升了测量速度，满足实时性的要求。并针对最小二乘法重建温度场缺失的问题，提出以最小二乘法重建结果为基础，使用Reflect Sigmoid 函数进行插值的两阶段重建算法。实验结果表明，本文设计的超声波测温系统可以快速得到准确超声波飞渡时间，结合本文提出的Reflect Sigmoid 函数插值算法，可以得到较为准确的温度分布图像。