基于ICA的电力系统稳定器系统设计
2019-11-20郭克,肖宁
郭 克,肖 宁
(西安工业大学,陕西 西安 710021)
0 引 言
近年来,我国电网互联规模不断扩大,其复杂程度也随之提升。因此,导致电力系统产生低频振荡的频率逐渐提高,其造成的电网事故不断发生。目前研究发现,电网区域事故产生最主要起因就是低频振荡弱阻尼,这一事故的起因所造成的区域振荡通常会使得一到多个地区发生停电事故,严重的情况下甚至会导致电力系统的分解与停运[1-5]。目前电力系统中抑制低频振荡的主要方法有以下几点:
1)在发电机励磁系统中加装电力系统稳定器(Power System Stabilizer,PSS)[6];
2)采用 HVDC 输电[7-8];
3)采用柔性多状态开关控制阻尼[9-11];
4)发电机组调速阻尼控制[12-13]。
在以上方法当中,与低频振荡的关联性较高的发电机组上安装电力系统稳定器,是目前电力系统中抑制低频振荡的主要方法。PSS 具有其相位超前补偿的功能,将一定限度地实现对电力系统阻尼的有效控制。但由于系统中的低频振荡和负阻尼所具有的特性并不相同,故会产生PSS 无法彻底抑制电力系统低频振荡的情况[14]。
由于互联电力系统的复杂程度较高,传统的PID 整定范围难以满足实际需要,而分数阶PID 因其能够有效抑制电力系统谐波,增强电网鲁棒性而被广泛应用到电网控制系统设计中。本文针对传统PID 控制器在电力系统稳定器系统中即时追踪能力弱、难以迅速抑制电力系统中产生的低频振荡的局限性,设计了基于帝国竞争算法(Imperialist Competitive Algorithm,ICA)的电力系统稳定器系统。该系统采用分数阶PID 控制器进行反馈控制,然后利用ICA 对系统进行优化[15],最后在励磁控制系统中对该PSS 系统的控制效果进行验证。结果表明,本文设计的基于ICA 的电力系统稳定器系统能够有效抑制电力系统低频振荡,跟踪性与鲁棒性均能满足工程实际的需要。
1 基于分数阶PID控制器的电力系统稳定器系统
1.1 分数阶PID控制器设计
分数阶PID 控制器是整数阶PID 控制器的进一步演化,主要应用于复数域,是近年来使用较多的一种较为新式的控制器。
整数阶PID 控制器的表达形式为:

式中:kP表示控制器的比例增益;kI表示的是控制器的积分系数;kD表示的是控制器的微分系数。
而分数阶PID 控制器的表达形式为:

式中:u(t)表示的是输出的信号;e(t)表示的是输入的信号;λ表示的是积分阶数;μ表示的是微分阶数。λ>0,μ>0,且两者均为实数。
式(2)所对应的控制器传递函数表达形式为:

按照式(3)设计得到控制器对应的控制模型如图1所示。

图1 分数阶 PID 控制器控制模型Fig.1 Control model of fractional order PID controller
对比式(1)和式(3)可以发现,整数阶与分数阶两种PID 控制器中,后者增添了积分阶数与微分阶数两个参量,这使得控制器能够快速追踪电力系统稳定器系统的参量变动情况,较大地提升了系统的控制性能。同时,参数的增多使得控制器在选择参数时的复杂程度有所提升。
1.2 电力系统稳定器原理分析
电力系统中发电机组的建模通常使用的是三阶实用模型,励磁系统通常设定为静止形式,使用一阶惯性环节对其进行表达。将前两者与网络方程结合得到电力系统稳定器系统传递函数的框图,如图2所示[16]。

图2 单机无穷大系统传递函数框架图Fig.2 Framework diagram of transfer function of single machine infinity system
根据图2可得:

若令GPSS(p)超前的相位与滞后的相位相等,则电力系统稳定器的作用是令系统多一个与Δω相位一致的组成部分ΔT*e,从而导致正阻尼的生成。因此,对系统产生的低频振荡进行一定程度的抑制。电力系统稳定器传递函数框架图如图3所示[17]。

图3 电力系统稳定器传递函数框架图Fig.3 Framework diagram of transfer function of power system′s stabilizer
1.3 稳定器系统设计
电力系统稳定器可以额外实现励磁控制,通过给予励磁系统与转子速率差一致的电磁转矩分量来对系统产生的低频振荡进行抑制,从而确保电力系统稳定运行[18]。电力系统稳定器的传递函数为:

式中:kPSS表示的是系统的放大增益;Tw表示的是隔直时间常数;Ts1表示的是一阶超前时间常数;Ts2表示的是二阶滞后时间常数;Ts3表示的是二阶超前时间常数;Ts4表示的是二阶滞后时间常数[19]。
因为基于整数阶PID 控制器的电力系统稳定器励磁控制系统,在追踪电力系统数据时灵活性较低,从而难以满足系统抑制低频振荡的需要,这将无法保证电力系统的稳定运行。为了提升电力系统稳定器抑制低频振荡的性能,本文将PID 控制器的类型从整数阶修改为分数阶。基于分数阶PID 控制器的电力系统稳定器系统结构图如图4所示。

图4 基于分数阶PID 控制器的电力系统稳定器系统结构Fig.4 System structure of power system′s stabilizer system based on fractional order PID controller
由于电力系统稳定器的输入信号Δω可以准确实现追踪发电机负载,这表明当发电机负载增加时,系统的传递函数GPSS的放大增益同时增加,从而可有效提升电力系统稳定器励磁系统的励磁控制性能。由于本文在建立电力系统稳定器系统的传递函数模型时,令Δω作为系统输入信号。基于此,建立电力系统稳定器仿真模型,如图5所示。

图5 电力系统稳定器仿真模型Fig.5 Simulation model of power system′s stabilizer
将分数阶PID 控制器加入电力系统稳定器系统,使该系统安装到单机无穷大系统中。在仿真时采用阶跃响应来对系统中产生的低频振荡进行模拟,然后评估系统的稳定性。设计得到的系统数学模型如图6所示。

图6 基于分数阶PID 控制器的电力系统稳定系统数学模型Fig.6 Mathematical model of power system′s stabilizer system based on fractional order PID controller
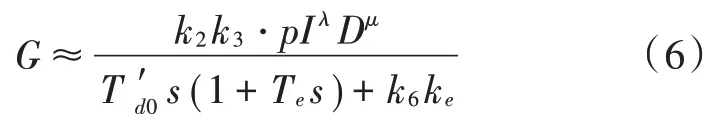
根据式(6)可得,系统传递函数的增益与滞后的相位角度和系数k2,k6有关,系数取值可利用文献[17]计算得出。传递函数增加情况与k2正相关,减小情况与k6正相关。
2 基于ICA的控制器参数优化
本文设计帝国竞争算法时采用Levy 变异算子,实现控制器的参数优化。与以往单一的帝国竞争算法相比,采用Levy 变异算子的帝国竞争算法能够实现快速收敛,精确度较高。改进后的帝国竞争算法能够大幅度降低工作量,提升参数的精确度。
2.1 帝国竞争算法
帝国竞争算法是近年来兴起的一种新型智能优化算法,其主要来源于社会行为的发展,核心内容是对殖民地同化制度与帝国竞争的制度进行一定程度的模拟。依据帝国竞争算法的发展流程优化控制器参数配置,如图7所示。

图7 帝国竞争算法流程图Fig.7 Flow chart of imperialist competitive algorithm
2.2 Levy变异算子
本文在采用帝国竞争算法优化控制器参数时,使用Levy 变异算子确保算法覆盖的区间范围更广。Levy 变异的实质是服从Levy 分布并给出随机数,当Levy 分布恰好在z=0 时实现对称关系,即可以得到分布的概率密度函数表达式,如下:

式中:α可以调节函数图像的形状,一般限定 0<α<2,本文选定α=0.3;γ代表尺度增大或减小的因子,定义其值大于0,为保证优化结果具有一般性,尺度因子γ值选定为1。此时,Lα,1可表示为Lα。
2.3 考虑Levy变异算子的ICA
在帝国竞争算法中,帝国主义集团的查找历程与优化程度有关。由于各殖民地均在向帝国主义国家(Imperialist State,IS)靠近,当 IS 处于局部的最优状态时,附属的殖民地同样有较大可能处于同等状态,即导致早熟状况的发生。随之而来的则是种群的分散性消失。因此,本文针对IS 将考虑增加相应的变异算子。设IS 的代表变量为则将执行变异的流程为:
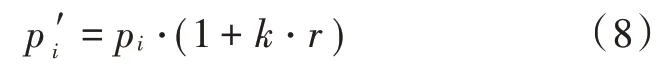
式中:r表示服从Levy 分布得到的随机数;k表示的是代表尺度大小的参数。变异处理面向向量中所有维度,若求解结果质量提升,便表明变异处理较为成功。因此,为提升变异处理成功的概率,各维度需实施5 次变异操作。
2.4 控制器参数优化
本文为整定控制器参数,设定了相应的最小化性能指标。文中采用向量表示帝国主义国家,表达形式为:

式中,P表示的是控制器的控制参数,在仿真时对参数的取值范围进行限定。
为更好地满足系统抑制低频振荡的要求,实现整定控制器参数的目标,本文所设定的最小化性能指标为:

式中:β表示的是加权系数,设定β=1;MP表示的是最大偏差;ESS表示的是稳定时的系统误差;tr表示的是上升时长;ts表示的是系统调整时长;J(P)表示的是惩罚函数。
采用最小化性能指标相较于其他误差积分的原则,能够较大程度上降低系统开始运行时的误差加权,且针对后期产生的较小误差能更优的进行修正。从而使系统的最大偏差降低,令系统的暂态响应衰减速率得以降低。另外,若控制器无法维持闭环系统的稳定运行,则表明所设计的控制器无法实现有效控制。此时,需要对其施加惩罚。由此可以得到,适应度函数为:

式中,L无限趋近于正无穷。当J(P)控制其实现最小化目标时,即可判定控制器达到最优。
本文将考虑Levy 变异算子的帝国竞争算法应用到分数阶PID 控制器的模型搭建中对其进行一定程度的优化。其具体流程如图8所示。
3 仿真验证
仿真时设定传递函数为:
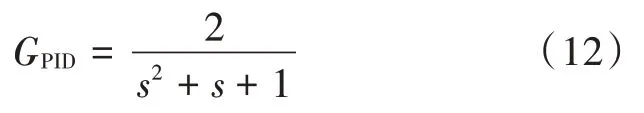
在进行仿真时针对系统的低频振荡分别采用P 控制、PI 控制、PD 控制与PID 控制执行控制操作,从而测试4 种控制方法的响应性能,进而分析其控制功能的有效性。
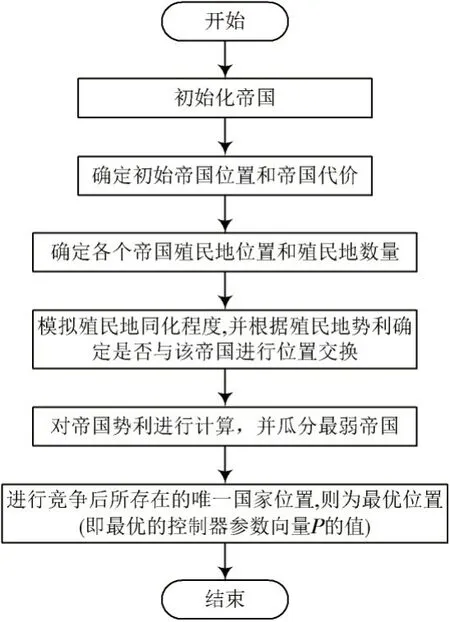
图8 控制器优化流程Fig.8 Optimization flow of controller
各类控制器的阶跃响应性能对比如图9所示。系统采用P 控制时最大偏差较大,此时系统产生低频振荡;而系统采用PI 控制降低最大偏差的效果较好,然而此时系统的消去静差的时长会有一定程度的增长;系统采用PD 控制能够提升系统响应的速率,然而同时抑制扰动的性能有所下降;而系统采用PID 控制能够大幅度降低自身的响应时长与最大偏差,提升响应的速率。故经过对比可得出结论,PID 控制的相对控制性能最优。

图9 各类控制器的阶跃响应性能对比Fig.9 Comparison of step response performances of various controllers
采用帝国竞争算法对控制器参数进行优化,得到各优化参数如表1所示。
阶跃响应曲线对比图如图10所示。PSS 系统分别采用整数阶PID 控制器与基于ICA 的分数阶PID 控制器抑制系统低频振荡时的阶跃响应曲线对比图。其中,PID-PSS 表示基于整数阶PID 控制器的电力系统稳定器,ICA-PID-PSS 表示结合帝国竞争算法设计得到的基于分数阶PID 控制器的电力系统稳定器。由图10可知,前者的最大偏差为9.85%,上升所需用时为0.42 s,系统稳定所需用时为1.21 s;后者的最大偏差为35.8%,上升所需用时为0.125 s,系统稳定所需的调节用时为0.41 s。因此可以得出结论,结合ICA 的基于分数阶PID 控制器的电力系统稳定器能够更优地抑制电力系统产生的低频振荡。同时具有良好的抗干扰能力和追踪控制能力,可有效维持电力系统的稳定运行。
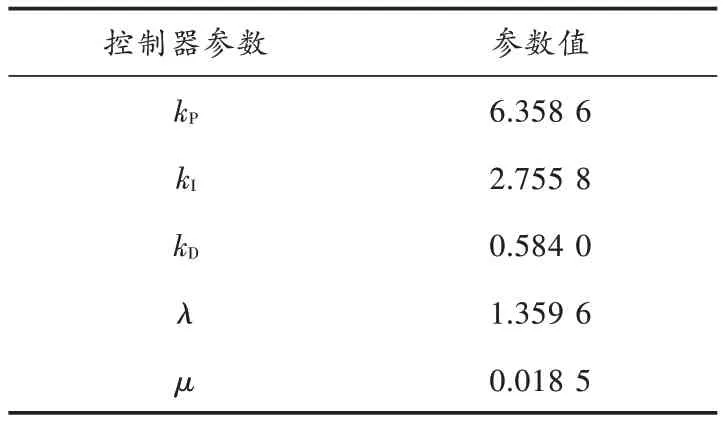
表1 分数阶PID 控制器优化参数Table 1 Optimized parameters of fractional order PID controller

图10 阶跃响应曲线对比图Fig.10 Comparison of step response curves
4 结 论
本文针对电力系统中传统的电力系统稳定器系统抑制低频振荡能力较弱的问题,在设计电力系统稳定器系统时,采用分数阶PID 控制器提升控制器参数整定的区域范围,从而改善系统控制的准确性。结合帝国竞争算法建立了基于分数阶PID 控制器的电力系统稳定器系统优化模型。在模型中对参数进行了优化配置,同时采用Levy 变异算子对算法进行改进,进一步发挥算法收敛速率快、优化准确等优势。根据对基于整数阶PID控制器的电力系统稳定器系统与结合ICA 的基于分数阶PID 控制器的电力系统稳定器系统对比,可以验证后者能够增强系统的控制性能,增进电网的阻尼特性。从而针对系统产生的低频振荡能够进行快速抑制,取得较好的控制效果,且大幅度提升了电力系统运行的稳定性。仿真结果表明,本文所提出的基于ICA 的电力系统稳定器系统可以满足工程实际应用。
