基于AHP的高校贫困学生精准评定方法
2019-11-19孙媛媛杨明亚刘红兵
孙媛媛,杨明亚,陈 俊,刘红兵
(安徽新闻出版职业技术学院机电信息系,安徽 合肥 230601)
层次分析法(Analytic Hierarchy Process,简称AHP)是一种规范化、系统化、层次化的管理学分析方法.它在理论上将问题分解成目标、准则、指标、方案等若干层次,建立多个层次的判断矩阵模型,各个层次都是用比较的方式得出一个权重,各权重组成矩阵,最后计算出矩阵的特征向量.为了公平、公正地开展高校贫困学生资助工作,使国家的贫困助学资金精准地资助到每一位贫困大学生,在资助工作中,可以利用AHP量化贫困大学生的家庭经济状况,建立判断矩阵,再通过数学建模对评定方案进行分层,用Matlab软件完成数值计算,从而为家庭贫困大学生的评定工作提供科学依据[1-2].
1 层次模型的建立
在贫困大学生的精准资助过程中,将资助问题分成4个层次,即目标层、准则层、指标层和方案层[3-4],具体见表1.

表1 贫困大学生评定决策层次
2 模型计算
2.1 判断矩阵的构建
为了使判断矩阵更具说服力,聘请参与贫困大学生评定工作的专家对层次模型每一层中不同的指标进行比较,分析其相对重要程度并给出具体的数值,再用这些数值构建判断矩阵A.根据AHP的原理,Aij=ai/aj,表示第i行问题要素与第j列问题要素的相对重要性度量值,若度量值为1,则说明要素ai与要素aj的重要程度一样,若度量值为3,则说明要素ai比要素aj稍微重要.Aji是要素aj与要素ai相比较,Aji=aj/ai,Aij与Aji是互为倒数的关系,即Aij=1/Aji.
制定贫困大学生评定要素征询意见表,向每位专家提供贫困大学生精准资助所需的材料,之后对专家给出的数值进行分析和汇总,并将首次统计结果反馈给专家,专家根据反馈意见和建议去修正度量值.进行多次的征询和意见反馈后,统计出Aij的数值.专家可以按照1~9的度量值来比较要素ai和要素aj的重要程度,其值用Aij或Aji表示.
2.2 评价指标权重的确定
通过问卷调查的方式,请15位专家按同等重要、稍微重要、明显重要、非常重要和极端重要等5个标准的AHP标度,给出贫困大学生评价指标权重的数值.贫困大学生评价指标权重调查表如图1所示.
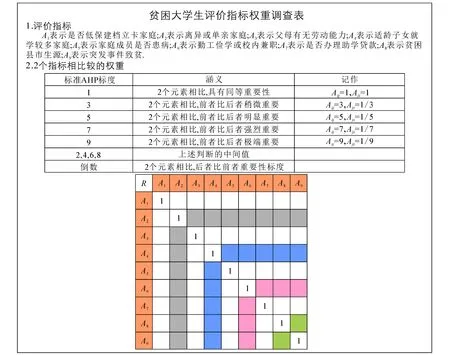
图1 贫困大学生评价指标权重调查表Fig. 1 Questionnaire on Index Weight of Poverty-Stricken Students
(1)评价指标.A1表示是否低保建档立卡家庭;A2表示离异或单亲家庭;A3表示父母有无劳动能力;A4表示适龄子女就学较多家庭;A5表示家庭成员是否患病;A6表示勤工俭学或校内兼职;A7表示是否办理助学贷款;A8表示贫困县市生源;A9表示突发事件致贫.
(2)2个指标相比较的权重.对15位专家给出的权重取平均值,最终得到贫困大学生的评价指标权重,如A12=(1+1/2+1/3+1/2+1/3+1/2+1/4+1/2+1/2+1/4+1/3+1/2+1/2+1+1/2)/15=1/2,A13=(1/4+1/5+1/4+1/4+1/5+1/3+1/4+1/3+1/2+1/4+1/4+1/2+1/2+1/3+1/5)/15≈1/4.
2.3 矩阵特征值的求解
通过贫困大学生评价指标权重构建判断矩阵A,得到
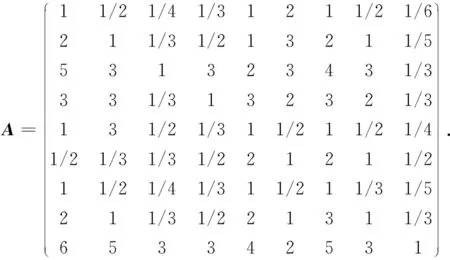
为了便于计算,利用Matlab软件求解矩阵A的特征值和特征向量(图2).
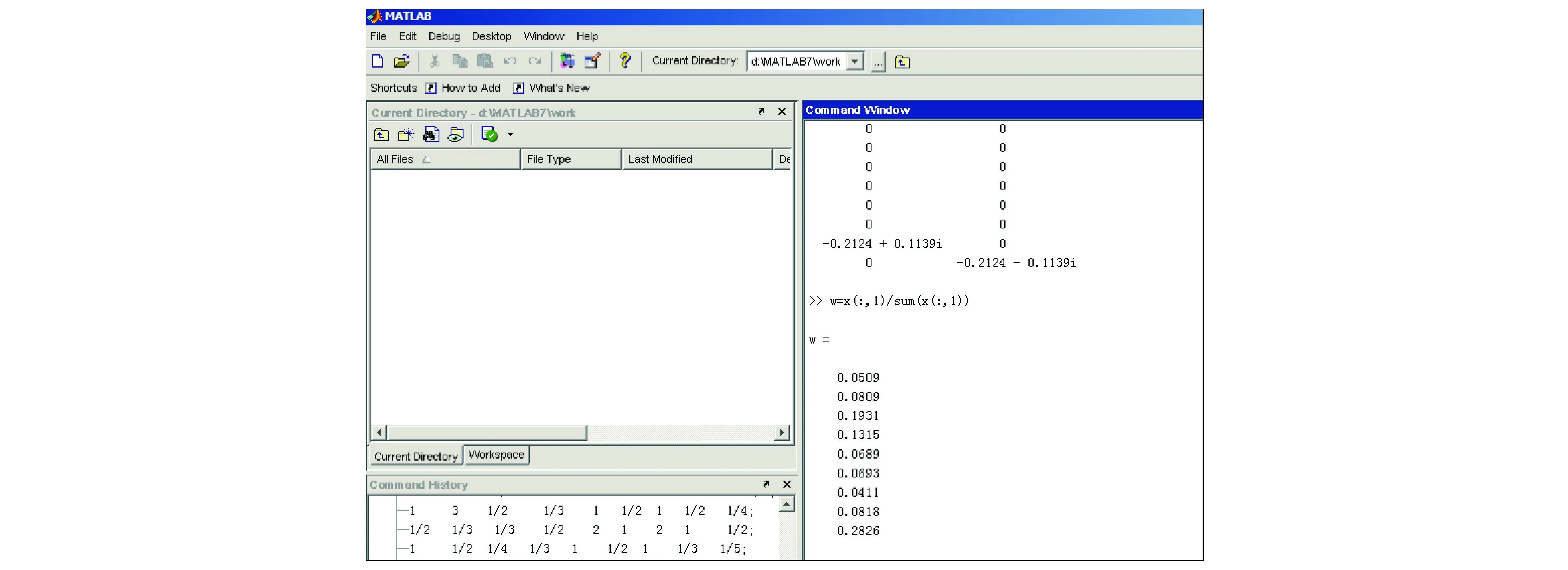
图2 求解矩阵A的特征值和特征向量Fig. 2 Eigenvalues and Eigenvectors of Matrix A Solution
假设W(2)是第2层的矩阵A的特征向量,则
W(2)=(0.050 9 0.080 9 0.193 1 0.131 5 0.068 9 0.069 3 0.041 1 0.081 8 0.282 6)T.
再利用公式
(1)
计算最大特征值.令d=A×W(2).用Matlab软件计算d,得到
d=(0.510 4 0.810 2 1.934 5 1.317 7 0.690 2 0.694 9 0.411 9 0.819 2 2.831 4)T.
根据(1)式,得到最大特征值
λmax=(0.510 4/0.050 9+0.810 2/0.080 9+1.934 4/0.193 1+1.317 7/0.131 5+0.690 2/0.068 9+
0.694 9/0.069 3+0.411 9/0.041 1+0.819 2/0.081 8+2.831 4/0.282 6)/9=10.019.
3 一致性检验
3.1 判断矩阵的一致性检验
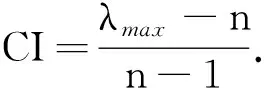
在计算中,只要矩阵的一致性比率CR≤ 0.1,就可以完全接受判断矩阵的一致性检验;反之,要重新建立两两比较矩阵.因为最大特征值λmax=10.019 5,所以CI=(10.019 5-9)/8=0.127 4.当矩阵的阶数或维数较大时,应对矩阵的一致性放宽判断条件,而本研究中的判断矩阵为9阶矩阵,故用修正系数RI进行修正.AHP中的随机一致性指标RI是已知的(表2).

表2 随机一致性指标RI
由CR=CI/RI,可以得到CR=0.127 4/1.45=0.008 75<0.1,由此可知判断矩阵A接近一致性要求,求出的权重是合理的.若CR≥ 0.1,则要对判断矩阵A进行修正或调整数值,直到CR≤ 0.1为止[7-9].
3.2 大学生贫困状况的判别

图3 9个评价指标对应的标准的判断矩阵Fig. 3 9 Judgment Matrices
以王倩、张俊、李云3个大学生为研究对象:王倩来自单亲家庭,与奶奶一起生活,奶奶的岁数较大且无固定收入;张俊来自父母离异的家庭,与父亲一起生活,父亲的身体不好且无工作;李云来自多子女家庭,母亲在农村,父亲在外地打工,家庭经济收入较少.现根据3位学生的家庭状况来评定哪位学生最贫困.具体评定步骤如下:
(ⅰ)建立判断矩阵.9个评价指标对应的标准的判断矩阵如图3所示.
(ⅱ)利用Matlab软件计算各矩阵的特征向量.计算结果为:
判断矩阵B1的特征向量W(B1)=(0.146 3 0.531 7 0.322 0)T,
判断矩阵B2的特征向量W(B2)=(0.124 3 0.358 6 0.517 1)T,
判断矩阵B3的特征向量W(B3)=(0.569 5 0.333 1 0.097 4)T,
判断矩阵B4的特征向量W(B4)=(0.614 4 0.268 4 0.117 2)T,
判断矩阵B5的特征向量W(B5)=(0.287 2 0.634 8 0.078 0)T,
判断矩阵B6的特征向量W(B6)=(0.095 3 0.249 9 0.654 8)T,
判断矩阵B7的特征向量W(B7)=(0.673 8 0.100 7 0.225 5)T,
判断矩阵B8的特征向量W(B8)=(0.457 9 0.416 1 0.126 0)T,
判断矩阵B9的特征向量W(B9)=(0.658 6 0.185 2 0.156 2)T.
(ⅲ)计算各判断矩阵的最大特征值λmax和一致性比率CR,结果见表3.

表3 最大特征值λmax和一致性比率CR
由表3可知,B1—B9的一致性比率CR均小于或等于0.1,说明判断矩阵的一致性满足,求出的权重是合理的.即第3层的特征向量
(ⅳ) 计算权向量.第2层的矩阵A的特征向量
W(2)=(0.050 9 0.080 9 0.193 1 0.131 5 0.068 9 0.069 3 0.041 1 0.081 8 0.282 6)T,
根据公式W=W(3)×W(2),利用Matlab软件进行计算,得到权向量W=(0.485 9 0.307 3 0.206 9)T.矩阵的一致性比率
CR=(0.050 9×0.058 2+0.080 9×0.054 0+0.193 1×0.013 0+0.131 5×0.009 1+
0.068 9×0.046 7+0.069 3×0.010 8+0.041 1×0.042 6+
0.081 8×0.004 6+0.282 6×0.014 5)=0.017 131 4≤0.1,
故层次总排序可以通过一致性检验.
(ⅴ)精准评定贫困大学生.从W=(0.485 9 0.307 3 0.206 9)T可知,王倩同学是最贫困大学生.
4 结语
在高校贫困学生的评定过程中,笔者综合考虑多方面因素,建立了贫困大学生评价指标体系,构建了评价层次结构模型,并利用贫困大学生的数据平台收集并统计各项指标的权重,从而构建了判断矩阵,再利用Matlab软件求解矩阵的特征值和特征向量,计算出学生的最终贫困数据,即计算权重得分.AHP避免了人为主观因素的干扰,使评定过程更客观、公正,达到了精准资助的目的.
