致密砂岩储层微观孔隙结构的分形研究

王 妍,马 瑶,王若谷,陈永振,孙博亚,李文厚,吴 越

(1.西安石油大学 石油工程学院, 陕西 西安 710065;2.陕西延长石油(集团)有限责任公司 研究院,陕西 西安 710006;3.陕西省能源化工研究院,陕西 西安 710069;4.西安科技大学 地质与环境学院,陕西 西安 710054;5.西北大学 地质学系，陕西 西安 71069;6.长庆油田分公司 第十一采油厂,甘肃 庆阳 745000)

储层非均质性决定着储层物性的好坏,对储层预测也有重要影响。储层的孔隙分布于三维空间,但又不充满三维空间,空间分布具有统计自相似性。分形理论提供了一种简单的方法，将大尺度的变化与小尺度的变化联系起来,反之亦然[1-2]。由于其在表征复杂、不规则特征方面的优势,已逐渐被引入到分析孔隙结构的复杂性和评价储层的非均质性中[3-4]。自Katz and Thompason利用扫描电镜对砂岩的孔隙进行分形分析以来[5],众多学者研究认为，孔隙结构在一定的孔径范围内表现出良好的分形特征,其特征可用分形维数来表征[6-11]。

分形维数求解方法多样,如Friesen等[12]和Yang等[13]用导数法得到了分形维数与饱和度线性方程的关系,并计算了分形维数;贺承祖等[8]和张国辉等[14]从毛管压力和湿相饱和度的线性方程出发,推导出岩石的分形维数;Krohn[4]采用扫描电子显微镜观察岩石样品的截面并求取分形维数;贾芬淑等[15]创建了根据图像处理技术测定砂岩孔隙结构的分形维数的方法;彭瑞东等人[16]提出了基于CT图像的灰度图像分形维数的计算方法。

不同方法计算的岩石分形维数也不同,目前常用的计算方法主要有两类,一类是基于压汞资料的分形维数求解[8,14,17-22],另一类是基于图像数据的分形维数求解[4,15-16, 23-29]。相对于图像数据,压汞资料便于获取。现有研究大多根据毛细管压力曲线来计算储层分形维数,虽然有其优点,但也存在数据平滑等缺点,因此它们不能显示细节和局部非均质性[2];而基于成像分析技术的分形与多重分析技术为描述储层孔隙空间分布提供了新方法,从而为定量评价储层的储集性能提供新的认识[16, 25-26]。

目前，对储层微观结构的分形理论研究主要集中在中、高渗等常规储层方面,针对致密储层，尤其是致密砂岩的研究较少。为此，本研究以鄂尔多斯盆地陇东地区长7致密砂岩油藏的真实岩心作为研究对象,分别利用基于压汞资料的MIFA法及基于CT扫描技术的分形盒维数研究，对孔隙空间的分形特征进行分析和描述,并对两种方法计算的分形维数之间的差别进行分析与探讨。

1 分形维数的表征方法

1.1 压汞资料法

MIFA法是以毛管压力曲线为资料,采用分形理论研究储层孔隙结构的一种计算方法。非润湿相注入多孔介质时,表面张力阻止非润湿相进入孔隙,需额外施加压力才能将非润湿相液体注入岩石孔隙中,这个额外压力即毛管压力。1998年，贺承祖等根据毛细管压力曲线建立了岩样中的润湿相流体饱和度与毛细管压力之间的关系[8],即

(1)

式中:pc为任意孔隙半径所对应的毛细管压力,MPa;pmin为储层岩石最大孔径rmax对应的毛细管压力,即突破毛细管压力,MPa;Sw为毛细管压力pc时储层岩石中润湿相的饱和度;D为分形维数。

由式(1)可知,如果岩石孔隙结构符合分形特征,则储层中的润湿相饱和度与毛管压力之间应满足幂函数关系。对式(1)两端取对数,可得

lgSw=(3-D)lgpmin+(D-3)lgpc。

(2)

由式(2)可知,润湿相饱和度与毛管压力在双对数坐标系下为一条直线,如储层岩石孔隙具有分形结构的性质,则根据毛细管压力资料可知,lgSw与lgpc之间呈线性相关关系,直线的斜率为D-3,据此可以得到岩石孔隙的分形维数D。

1.2 CT图像分析法

传统的储层地质室内实验，如普通薄片、铸体薄片、扫描电镜等能够揭示岩石微观孔隙结构,但是具有一定局限性。如普通薄片和铸体薄片得到的二维图像只是对样品单一层面的取样,无法反映立体结构;扫描电镜获得的图像空间延续性差[30-31]。近年来，CT技术在石油行业广泛应用,可以精确检测储层样品的内部结构,反映储层微观孔隙的三维高精度结构[32-34]。通过对CT图像进行分析,也可计算出分形维数。CT图像为灰度图像,目前常用手段是将灰度CT图像转化为黑白二值图像再计算分析。

在实际操作中,盒维数由于其简易性和可操作性被频繁使用,基于二值图像的盒维数算法(box-counting method,BC算法)主要过程步骤如下。

1) 读取一幅M×N像素的二值图像,每个像素点非即1,通常白色像素表示孔隙;

2) 用大小s×s像素的网格(盒子)去完全覆盖二值图像,分割比例r=s/M;

3) 任何一个网格块只要包含目标对象就被认为是被占用(可计数)的网格块,进而统计总共被占用的网格块数Nr;

4) 改变s的大小不断重复上述过程,可得到一系列(Nr,r);

5) 在双对数坐标中用最小二乘法拟合[logNr, log(1/r)],所得的斜率即为该图像的分形维数。

2 结果与讨论

2.1 孔隙描述

所选样品碎屑颗粒以石英为主,长石次之,长石颗粒以斜长石居多,蚀变中等偏多,常可见长石溶孔。粒间填隙物以泥铁质为主,可见硅质胶结和钙质胶结。硅质胶结较少,以石英次生加大为主,钙质胶结发育较多,以方解石胶结为主。黏土矿物主要以伊利石、绿泥石为主。样品孔隙发育一般,多为孤立状,连通性较差,储集空间类型以非组构选择性孔隙(其中，粒间溶孔体积分数为1.5%，长石溶孔体积分数为0.8%)及少数组构选择性孔隙(如粒间孔体积分数为1%)为主(见图1),样品还发育微裂缝,平均缝宽约16 μm，样品可见伊利石、绿泥石及自生石英充填孔隙。对样品进行薄片观察可知，粒间溶孔体积分数为1.5%,长石溶孔体积分数为0.8%,粒间孔体积分数为1%。样品压汞法测定孔隙度7.94%,渗透率0.102×10-3μm2,为致密储层。

2.2 基于MIFA法的分形维数

在三维欧氏空间中，孔隙结构的分形维数介于2与3之间。分形维数越接近2,孔喉表面越光滑、孔隙结构越均匀、均质性越强。分形维数越接近3,孔喉表面越不光滑、孔隙结构越不均匀、非均质性越强。

图1 主要孔隙类型Fig.1 Main pore types

根据孔隙结构分形维数的适用条件,验证了该致密砂岩样品符合分形特征,即样品的含水饱和度与压汞毛管压力在双对数坐标系上是一条显著的直线(见图2),拟合直线斜率2.098 24,直线判定系数0.969 29。这说明孔隙结构整体具有“单段型”分形特征,其孔喉大小分布较集中,呈似单峰形态(见图2)。无论是压汞法测量的该样品微观均质系数0.389,还是通过对研究区该层位22个样品统计的均质系数0.368 3,均表明储层非均质性变化不明显,为中等非均质性,与分形维数反映的微观孔隙结构的非均质程度结果相吻合。

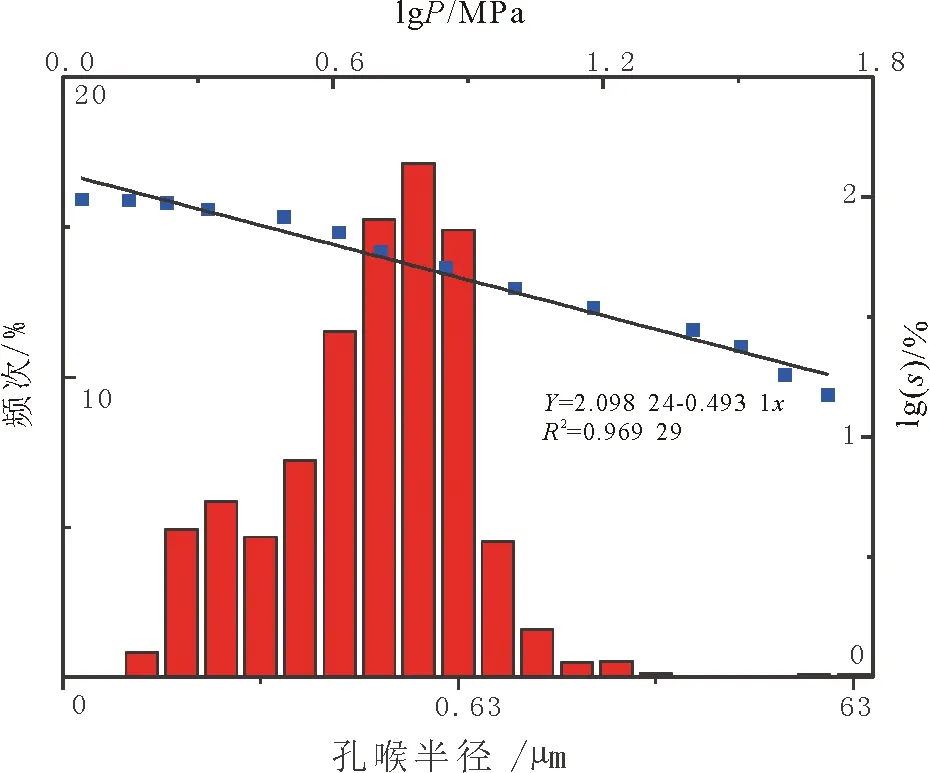
图2 MIFA法分形特征及孔喉半径特征Fig.2 Fractal characteristics of MIFA method and pore& throat radius characteristics

设lgSw=y,lgpc=x,(3-D)=a,lgpmin=b,则公式(2)变为y=ab-ax。利用回归拟合法可得到精确的分形维数D,D=2.507。

2.3 基于BC算法的分形盒维数

应用MATLAB编程对样品CT图像进行分形盒维数的计算。

1)图像预处理。为了计算分形维数,需要对CT图像进行一系列处理,包括亮度调节(见图3,4a)、图像剪裁(见图4b)、阈值分割等,从而获取可进行分形分析的二值图像。

使用Matlab程序将图像RGB值乘以系数n,可得到不同亮度增强的图像。如图3所示,n为1.5～2.5时，图像亮度依然较暗(见图3b～d),n为3.5～4.5时(见图3f～h)图像亮度已经过亮,因此选择n=3时(见图3e)亮度调节后的图像。图像亮度调节后的图像剪裁不仅可剪裁掉无效部分,保留图像中心圆形区域,还可消除CT扫描过程中图像边缘伪影的影响。最后，在阈值分割过程中,应用Otsu算法进行分割,所获得的二值图像如图4c所示。

图3 不同亮度的CT图像Fig.3 CT images of different brightness

图4 CT图像的预处理过程Fig.4 Pre-processing of CT images

2)分形分析。在三维欧氏空间中，平面内的分形曲线的分形维数介于1与2之间。因此二值图像的盒维数范围为1～2。数字图像盒维数的计算是基于对像素矩阵的分析,表象上看是反映了研究对象对平面的占有情况,分形维数越大,越趋向于充满整个平面,本质上来说，是反映了关心区域趋向于沿整个图像范围分布还是趋向于沿某条直线分布[24]。

作为示例,利用Matlab编程语言研究了鄂尔多斯盆地陇东地区某长7油层组致密砂岩孔隙结构的分形特征。通过对岩石样品断层扫描,获得了1 000张左右的32位切片图像,图像分辨率为0.724 μm,图像间隔1个像素点。CT图像中包括粒间孔、溶孔等关心区域,通过一系列图像分析处理,将这些孔隙提取出来,并转化为黑白位图。

灰度图像被转化成黑白位图后,可通过对图像中黑白像素的统计来计算孔隙度(白色代表孔隙,黑色代表固体颗粒),计算公式如下:

(3)

其中：Pixelswhite代表孔隙总像素个数；Pixelwhote为图像的总像素数。

实测孔隙度为9.86%,计算孔隙度为10.02%，误差为1.6%，结果表明，所选用的阈值分割算法是合理有效的。

本次研究通过应用几何序列选取盒子的尺寸序列。具体来说,剪裁后图像尺寸为400×400,盒子序列s满足1≤s≤M/2,即尺寸盒子范围s={1,2,4,8,16,32,64,128}。计算所得CT图像盒维数为1.643。可以认为,这一维数反映了孔隙在平面内扩展分布的规律。数字图像盒维数越大,表明孔隙分布越不规则,也就表明储层非均质越强。因此,本样品孔隙结构非均质性一般,与基于MIFA法计算的分维数代表的物理意义相同。

3 结 论

1)通过压汞实验,拟合求取了鄂尔多斯盆地陇东地区某长7油层组致密砂岩样品的分形维数。

2)通过CT扫描获取该砂岩样品的高分辨率孔隙结构的灰度图像,继而通过图像分析技术对其二值分割,获取该图像的黑白位图,进而计算出黑白位图的计算孔隙度φ2,与实验孔隙度φ1相比,误差在5%以内,验证了阈值分割的合理性。

3)无论是基于MIFA法计算的分形维数还是基于CT图像计算的分形盒维数,都能反映孔径的分布特征。这两类分形维数的计算与同层位22块样品计算的均值系数结果相吻合,表明该样品孔隙结构较均匀,非均质程度一般。