联合结构预测和运动补偿的视频自适应压缩感知

杨森林,万国宾

(1.西安文理学院 陕西省表面工程与再制造重点实验室, 陕西 西安 710065;2.西北工业大学 电子与信息学院, 陕西 西安 710072)

在未来无线多媒体视频传感器网络系统中,将大量采用低成本和低复杂度的视频传感器。当这种低功耗设备大规模部署时,常规的H.26x预测视频编码在这种视频传感器编码应用中就会遇到严峻挑战[1]，传统预测不适合低功耗无线视频传感器编码。Candes和Romberg提出的压缩感知(CS)理论[2],突破了传统的奈奎斯特-香农采样定理的限制,能够实现信号的压缩采样，并通过优化算法对原始信号精确重构。视频压缩采集所需计算能力小、功耗低和带宽窄,在接收节点完成视频信息重构,非常适合于移动视频、无线多媒体网络等应用场合。根据CS理论,实现流媒体系统视频的有效压缩和精确重建需要对视频信号进行有效的稀疏表示和压缩测量。在视频压缩研究中,通常采用离散余弦变换(DCT)或离散小波变换(DWT)对视频帧进行稀疏表示[3]。通常,由于全局压缩采样观测矩阵所需的存储需求大、重构计算复杂度高,一般对视频进行分块压缩感知[4-5]。同时,将视频划分为由关键帧和WZ帧构成的图像组(GOP)序列依次进行压缩采样和重构。然而,对采样率低的WZ帧,常规单帧重构算法重构质量较差。

为改善逐帧重构的质量,研究人员针对视频序列的时间相关性进行了探索。首先,Larson等采用基于帧间相关性的三维CS重构方法[6],把一组MRI视频帧作为一个3D数据体进行重构。3D重构增加了数据维度,加剧了计算复杂度和内存需求。Vaswani和Lu采用了已知的稀疏模式,对当前视频帧采用最小二乘或卡尔曼滤波进行基于残量预测的L1范数求解[7],也称为修正的CS(Mod CS)。其次,基于视频帧间的运动变化信息,Mun和Fowler将传统视频编码端的运动矢量信息引入到重构过程[8],提出采用两帧之间运动残量信息的CS重构方法。进而,基于高质量的参考帧进行运动估计与补偿,Chen等采用k-t空间的焦点欠定系统求解策略(k-t FOCUSS)[9-10],并用于动态MRI压缩重构，该算法通过高质量关键帧与非关键帧的残量进行双向运动补偿预测进行压缩重构,但k-t FOCUSS方法通常假设视频场景的运动变化是缓慢的。此外,Fowler等提出了基于稀疏变换域的多尺度压缩感知策略[11],对不同尺度采用多尺度非均匀采样。然而,实际应用中在变换域中多尺度非均匀压缩采样的硬件实现还比较困难。这些基于视频相关性预测对于缓慢变化的视频在一定程度上能提高压缩重构质量,但是，对于一般视频场景应用和硬件实现受限,同时计算复杂度也较高，因此,还需要开展进一步研究。

本质上,常规的一维或二维信号的压缩感知方法研究主要采用非自适应的线性映射策略,事先假设这些信号具有固定不变的稀疏特点,并用同样的正交基和测量算子进行固定采样率的压缩观测。然而,实际场景的视频帧信号往往是非平稳的,其场景稀疏性也是随场景内容变化的。其实,在压缩感知理论前提下,要求被测量信号具有很好的稀疏特性,这是有少量观测数据精确重构原始信号的先决条件,在很大程度上影响压缩观测过程所需的观测次数[12]。如果原始信号的稀疏特性变弱,就必须进行更多数目的压缩观测数据才可能完成高精度的信号重建,否则会严重影响信号的重构质量。显然,基于实践经验设定的非自适应压缩感知如果用于视频图像的压缩感知,将会严重影响视频帧的重构质量,降低了视频的观看体验效果。相关人员已开展了一些自适应压缩感知的探索。例如,立足于构造最优化测量算子的贝叶斯压缩感知[13],从理论上说能够获得最优化测量矩阵并实现自适应压缩感知。然而,贝叶斯压缩感知方法需用迭代过程优化测量感知算子,该过程复杂耗时、不适用于海量视频信号的实时感知。进而,一些文献采用统计模型实现信号稀疏度的自适应逼近,包括基于拉普拉斯先验模型、高斯混合模型、局部隐马尔可夫决策驱动模型以及自回归模型等稀疏性的逼近方法[14-17]。其实,这些视频信号稀疏性的逼近模型是否合理还需要进一步深入研究,给出可靠分析和论证。此外,还有文献变采样率的分块压缩观测策略,通过对同一场景不同区域使用非均匀分采样率来提高感知性能[18],但在实际场景中，难于对同一视频场景的不同区域采用非均匀采样率,因为会影响视频实时感知性能。本文在视频分块压缩感知基础上,给出了基于视频帧稀疏度近似测量的自适应压缩感知,并充分挖掘视频序列的结构相关性和时间冗余性,来提高视频GOP序列的重构质量。

1 分块压缩感知

1.1 分块压缩感知

对于任意一幅以列向量方式表示的视频图像f∈RN×1,假设采用正交基函数ψ∈RN×N能实现视频f的K稀疏表示,并用矩阵运算表示为f=ψμ,其中，μ∈RN×1，为视频f的稀疏投影系数,它可以用其中K≪N个非零元素进行近似逼近。根据压缩感知理论,对任何K稀疏视频帧图像f,都能够利用M=O(KlogN)个非自适应线性投影系数g=Φf实现精确重建,其中，g∈RM×1，为任意K稀疏视频f的压缩观测值,Φ∈RM×N(M≪N)为测量矩阵。通常情况下,这个非自适应线性投影变换是一个病态反问题,对应无穷多个解。要精确重建视频帧图像f,测量算子Φ和稀疏表示基函数ψ对应的传感矩阵Ω=Φψ必须满足2K阶约束等距性(RIP)条件[2],即Ω的2K列线性无关。如果不对视频帧进行分块处理,则属于全局压缩采样的方式,其所需的存储空间大、重建过程对应的计算复杂度非常高。

为降低视频帧压缩观测过程中存在的计算复杂度和减小存储器需求的问题,采用分块压缩感知(BCS)实现压缩采样。对于输入的任意一帧视频图像,将其划分为I个图像块,设每个子块包括B×B个像素,将这些图像子块矢量化排列和表示后,并用观测矩阵对所有矢量化表示结果进行压缩采样。令fk表示视频帧中第k个子块所对应的矢量表示形式,则该视频子块所对应的压缩观测结果为[4]

gk=ΦBfk,k=1,2，…,K。

(1)

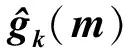
1.2 测量矩阵的选择

对视频帧的压缩观测而言,要完成高效的压缩测量与高质量重建,必须选取合适的观测矩阵ΦB。对于任意一帧视频,测量矩阵的选择应该综合考虑运算复杂度、存储空间需求、重构质量和硬件实现便利性等因素[19]。然而,大部分的测量算子在这些方面并不同时具备较好的性能。例如,伯努利矩阵和随机高斯矩阵作为观测算子时,具备很强的通用性能,并且能够基于较少数目的压缩采样结果完成原始信号的精确重建。然而,伯努利矩阵或随机高斯矩阵是非结构化矩阵,这些矩阵元素对应的存储空间需求大,重构复杂度高、重构速度慢。当然,有时也采用局部Fourier矩阵进行压缩观测,因为局部Fourier矩阵对应重构速度快,压缩观测的硬件系统实现复杂度低。但是，局部Fourier算子对应的通用性较差,元素所需的存储空间要求大。另外,某些二值稀疏矩阵也可用于压缩采样,而且具有较低的重构计算复杂度。但这些测量算子一般只与特定稀疏表示基函数线性无关,通用性较差。

结构化随机矩阵也能用于压缩观测,而且具有综合较优的性能。首先,结构化随机矩阵与所有的正交矩阵和大部分的稀疏信号都线性无关,具备很好的通用性能。同时,结构化随机矩阵作为测量矩阵时,能通过很少数目的压缩观测值高精度地和快速地重构原始信号。另外,结构化随机矩阵还能有效地分解为多个块对角矩阵或结构化子矩阵的乘积表示,便于视频序列的分块压缩采样以及滤波处理。目前,已经开发出了一些基于分块压缩采样的CMOS压缩成像集成图像传感器芯片。采用结构化随机矩阵,BCS将每个高分辨率的视频帧转化为数据点数很少的压缩观测结果,实现数据降维和压缩的目的。

1.3 重构算法

对于压缩感知而言,重构是一个关键的环节,重构视频图像的质量或精确度是选择重构方法的关键考虑因素之一。与此同时,重构算法的计算复杂度是重构策略选择的另一个关键考虑因素。对于重构方法,文献中给出较多的策略,诸如线性规划、全变分法、贪婪算法、梯度投影稀疏重构和阈值投影法等[20-22]。在这些方法中,线性规划和最小全变分法对应的重构过程计算复杂度高,即重构速度慢。梯度投影稀疏重构和贪婪算法的计算复杂度低、重构速度快,但经过相同迭代次数后重构视频帧质量较差。迭代阈值投影法相对比较折中,具备较低的计算复杂度,同时也具有较好的重建精度。为此,本文选择迭代阈值投影实现视频图像重构[23]。假设在第n步的迭代重构值为f(n),采用的阈值迭代函数为

(2)

(3)

χ(·)是迭代过程采用的阈值滤波处理函数,在迭代过程,对于第n次迭代重构结果f(n),采用阈值滤波变换处理,一般使用软阈值处理方法,即

(4)

其中：η为软阈值滤波所采用的阈值,并可采通用阈值方法对阈值η进行估算。文中引入阈值滤波处理函数χ(·)是为了消除视频帧分块压缩感知所导致的块效应问题。在空间域,还可使用3×3像素的局部维纳滤波进行平滑处理,以进一步消除分块效应,更好地提高重构质量。

对任意一帧视频图像的BCS压缩观测结果fi(i=1,2，…,I),阈值投影重构的步骤为：

初始化:输入压缩观测值fi(i=1,2，…,I)、测量算子ΦB、变换算子Θ、阈值参数η以及迭代误差阈值ε，然后，进入第1)步开始迭代;

2)对f(n-1)结果进行3×3模板的维纳滤波处理,结果记为f(n);

2 自适应感知策略

常规图像信号的压缩感知方法研究主要采用非自适应的线性映射策略,并事先假设这些信号具有固定不变的稀疏特点,并用同样的正交基和测量算子进行固定采样率的压缩观测。然而,实际场景的视频帧信号往往是非平稳的,其场景稀疏性也是随场景内容变化的。常规的非自适应压缩采样直接影响了视频帧的重构精度。如果能定量估算视频帧的稀疏性,就能避免盲目地选择压缩观测次数的问题,改善视频压缩重构的质量。

为有效改善视频帧的压缩测量并提高重构性能,确定较优的压缩观测数目,就必须定量近似计算视频帧的稀疏性。为此,将视频图像先进行二维稀疏变换,再对稀疏变换系数进行处理,完成稀疏性的估算。比如,可以采用二维离散余弦变换(2D-DCT)，其实,2D-DCT也是视频有损压缩编码的关键技术。对任一视频帧f的2D-DCT为

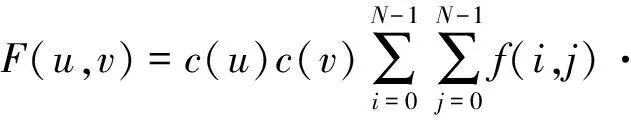
(5)

其中，i，j为空间域坐标,u和v为变换域坐标,系数

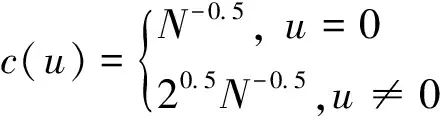
(6)

显然,2D-DCT是一种实数变换,分析基函数为二维余弦函数,广泛用于图像和视频的有损压缩编码,以及加水印信息隐藏算法。大部分图像的2D-DCT系数具有很好的稀疏特性。2D-DCT变换后的能量集中于较少的大系数上,而大部分系数接近于零或等于零。为了近似定量估计视频场景的稀疏特性,必须统计2D-DCT系数中占优势能量的较大系数占比。据此,给出一种近似的稀疏性估计方法:

1)用灰度变换方法将视频帧转换为灰度图,并计算2D-DCT变换;

2)将2D-DCT系数按绝对值递减的方式排序,并进行能量归一化处理;

3)确定优势能量阈值参数0≪α<1;

4)统计递减排序后的2D-DCT系数,优势能量为α所需的较大系数的占比。

图1(a)给出了PIG视频其中一帧,含有768×1024个像素,图1(b)为2D-DCT系数。图2为按照降序排列的50 000个较大的2D-DCT系数。设定能量阈值为0.99,最大的有效能量点数为13 005个,其中，总像素为786 432。该视频帧的稀疏度估算结果为0.095。实际应用中,为有效地近似估算稀疏性,需要选择一个合适的参数α,而不同参数α对应不同的稀疏度K。通常参数α在0.95至1之间选择。考虑到压缩测量过程中观测次数M≪N,结合M=O(KlogN)得

(7)

根据上文,K为视频图像的稀疏度参数,若K不满足式(7)，则稀疏度近似结果不合理,或者参数α选择不当。一方面,稀疏变换基函数选取不恰当,则二维变换系数的稀疏性能欠佳;另一方面,参数α选取欠佳,使观测次数M不合适,导致重构精度差或观测数目过多。

(a)视频帧 (b)DCT 2系数图1 PIG视频帧和其2D-DCT系数Fig.1 One frame of PIG and its coefficients of 2D-DCT transform

图2 降序排列后50 000个较大的2D-DCT系数Fig.2 The 50 000 larger 2D-DCT coefficients in descending order

按上述所提到压缩采样率选择方法,用16×16的像素进行分块压缩采样。为便于分析与对比,采样率分别选择了0.05, 0.10和0.15三种情况进行压缩感知,并用ITP方法对图1(a)进行重构,重构结果分别如图3所示,PSNR分别为27.5 dB,37.6 dB,和40.9 dB,SSIM分别为0.67,0.98,和0.99。实验结果表明,对这3种压缩采样率,重构后视频帧的PSNR和SSIM总体上随采样率的升高而变好。为了获到较好的视频重构精度,压缩采样率可设置为稀疏度估计结果的2～2.5倍。在此范围内,压缩采样率的变化虽然达到1.5倍,但实验结果表明重构视频对应的PSNR提高有限、且为非线性。同时,在满足稀疏性限定的最低采样率下,都能给出较好的重构结果,采样率越高图像重构质量越好。

图3 压缩采样率为0.05, 0.1, 0.15时的重构结果Fig.3 Reconstructed frames with subrate of 0.05, 0.1, and 0.15

3 帧内结构预测

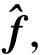
(8)

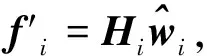
(9)

(10)

(ΦBHi)Tgi,

(11)

对于正则化参数λ,需要选择合适的值。实际应用中可以通过比较分析选择不同范围λ得到的预测结果,从中优选最合适的参数λ。

对帧内所有图像分块,通过结构相关性的预测,就能在一定程度上提高重构视频的质量。

4 帧间运动补偿

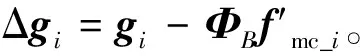
(12)

(13)

同样,利用参考帧和新的近似估计f′,又能进行更加准确的运动估计和运动补偿。

对一个GOP序列来说,设其有N个帧(N为偶数),第一个帧为关键帧,而其余N-1帧为WZ帧。对于关键帧用较高的压缩采样率,帧重构质量较高;而WZ帧则用较低的采样率,重构的质量较低。考虑以相邻的两个关键帧为起始帧，构成N+1帧视频序列,假设该序列已完成单帧压缩重构和结构预测,则可按如下顺序进行GOP运动补偿。

1) 顺序补偿:对第2帧到第N/2帧,以其前一帧作为参考帧,按顺序依次进行运动补偿;

2) 逆序补偿:对第N帧到第(N/2)+2帧,以其后一帧为参考帧,按顺序依次完成运动补偿;

3) 双向补偿:对第(N/2)+1帧,以其前一帧与后一帧做为参考帧,分别进行运动补偿,然后用这两种运动补偿的平均值作为运动补偿结果。

在结构预测的基础上,按照以上方式可完成所有GOP序列的运动估计与运动补偿,进一步提高GOP序列的重构质量。总之,结合单帧压缩重构、结构预测和运动补偿的视频GOP处理流程如图4所示

图4 视频GOP序列处理流程示意图Fig.4 Processing flow for GOP sequence in the video

通常,运动估计和运动补偿计算复杂,比较耗时。在实际应用中,除采用高效率的实现算法外,还可以将处理算法并行实现。比如,为了提高运行效率,GOP各帧的单帧重构过程可并行实现,帧内结构预测也能并行实现。此外,运动补偿过程中的顺序补偿和逆序补偿两个过程之间也可并行实现。

5 仿真实验

对于文中给出的算法,用视频测试序列Susie进行测试。该视频序列每一帧尺寸大小为352×240,GOP大小为4,利用BCS算法对该序列进行了分块压缩采样,其中，关键帧采样率为0.7，WZ帧采样率为0.1。本实验所设计算法均在Matlab 7.1环境下编写调试,并在2.80 GHz CPU和4GB内存的单核PC机上运行。

对于GOP中每一帧视频,BCS压缩采样所用分块尺寸B为16,因为当分块尺寸为16时,块重构时间较小、同时重构精度也较好。对于该视频GOP序列,按照图4所示的方法流程,首先进行单帧压缩重构,再进行帧内结构预测,最后进行运动估计和运动补偿。图5给出了GOP中第4帧的原始图像、单帧压缩重构、结构预测和运动补偿重构结果。在各处理步骤中,GOP序列中每帧重构的峰值信噪比(PSNR)变化趋势如图6所示。

从视觉上分析,单帧压缩重构图像噪声较大、质量较差,在结构预测之后重构质量有了较小改善,而运动估计和补偿后的视频重构效果得到了较大的提升。对于关键帧而言,由于采样率高,重构精度也较高(39.55dB),在结构预测后PSNR提高为40.88 dB。对于WZ帧来说,由于采样率很低,所以，图5(b)所示的单帧压缩重构质量较差,PSNR为29.04 dB;图5(c)所示的结构预测小幅度地提高了重构质量,PSNR变为29.95 dB;图5(d)所示的运动补偿较大幅度地提高了图像重构质量,PSNR增至36.76 dB。通过结构补偿,WZ帧的PSNR提高了1～1.5 dB，而运动补偿后,WZ帧的PSNR提高了6 dB左右。

图5 对Susie视频GOP序列第4帧的重构结果Fig.5 Reconstruction of the 4th frame of the GOP sequence in Susie video

图6 Susie视频GOP序列的重构PSNRFig.6 PSNRs of reconstructed GOP sequence in Susie video

另外, 还采用其他多种标准视频测试序列进行了测试, 表1给出了对5种不同标准视频序列的关键帧恢复的PSNR, 表2给出了对WZ帧重构的PSNR。 表1表明,通过帧内的结构预测, 关键帧的重构质量有(1～5 dB)不同程度的改善。 表2表明,通过帧内的结构预测,WZ帧的重构质量有(1～2 dB)不同程度的改善,在运动补偿处理后,WZ帧的重构质量进一步提高,为3～7 dB。

不同视频序列仿真结果表明,在视频GOP序列的压缩采样与重构处理中,由于采样率低,单帧重构的WZ帧PSNR低,通过结构预测和运动补偿,有效地提高了WZ帧的重构质量。同时,结构补偿也能改善关键帧的重构质量。

表1 关键帧的重构PSNRsTab.1 PSNRs of reconstructed key-frames dB

表2 WZ帧的重构PSNRsTab.2 PSNRs of reconstructed WZ frames dB

此外,当视频的关键帧采用较高压缩采样率(0.7),非关键帧采用0.1～0.5之间5种不同的压缩采样率时,采用不同方法进行重构,对10次重构过程中的平均PSNR值进行了对比。对于Foreman视频,图7给出了采用6种不同方法的重构PSNR值。图7中,采用的6种方法包括了三维分块重构(3D)、修正的压缩感知重构(Mod CS)、多尺度压缩重构(MS)3种不涉及运动补偿的重构方法,以及基于两帧之间运动补偿的重构(MC),k-t Focuss焦点欠定求解方法,和本文给出的基于结构补偿和运动补偿的多预测重构。结果表明,在不同压缩采样率情况下,本文所提方法重构结果对应的PSNR最高,其次是基于运动补偿的分块压缩重构,修正的压缩感知重构精度最低,其余3种方法重构效果居中。

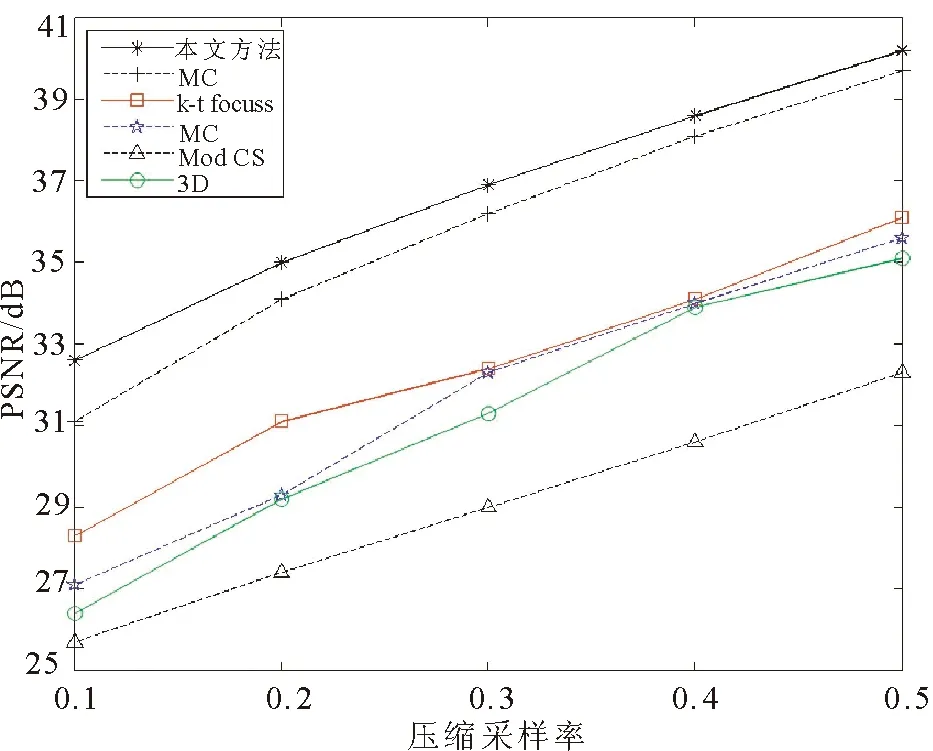
图7 Foreman视频GOP序列的重构PSNRsFig.7 PSNRs of reconstructed GOP sequence in Foreman video

6 结 论

提出了基于自适应压缩感知的视频GOP序列重构与质量改善策略。在视频GOP序列中,由于采样率低,单帧重构的WZ帧质量较差。所提视频自适应压缩感知方法相对于传统方法有效减少了采样个数、存储空间与传输带宽。帧内结构预测和运动补偿通过视频GOP序列的帧内和帧间相关性预测和补偿,提高视频重构质量。对不同视频序列,结构预测能将单帧重构视频的PSNR提高1～2 dB,而运动补偿进一步将重构视频的PSNR提高3～7 dB。文中所提方法利用视频帧内和帧间的相关信息进行预测补偿,有效地提高了视频GOP序列的重构质量。然而,该重构策略在实现过程中需要双向迭代重构,迭代步数较多时，其计算复杂度会增加,重构所需耗费的时间也会增加,是本文方法的不足之处,建议在提高重构过程中适当减少GOP序列双向预测的迭代次数。在今后的研究工作中,将开展基于深度学习的视频GOP序列的、智能感知与编解码研究,对不同视频序列都能实现快速高精度重构,以进一步改进视频GOP序列重构性能。