自动驾驶车辆的一种改进跟车算法

(东风商用车有限公司技术中心先行商品开发部,湖北 武汉 430056 ) (华中科技大学人工智能与自动化学院, 湖北 武汉 430074)

自动驾驶纵向控制技术起源于辅助驾驶(ADAS)中的ACC功能，但不同于自动驾驶的是ACC功能需要在一定速度下才能开启，而自动驾驶的纵向控制技术需要在车辆起步、车辆低速行驶时也必须作用，从而稳定舒适地跟随前方车辆。因此，笔者在目前常用于实现ACC功能的控制算法(如PID控制、LQR控制以及更为复杂的MPC算法[1～3])的研究基础上，研究了自动驾驶的纵向控制技术。

目前，关于自动驾驶的跟车算法[4，5]大部分采用3种最大速度的最小值作为自动驾驶的跟车速度，这3个最大速度分别为用户设定的最高车速，道路曲率限速，根据最大纵向加速度、最大纵向减速度和安全距离计算得到的最大速度。部分跟车算法[6，7]考虑了安全与动力舒适等多种评价指标，采用模糊分析、深度学习等非规则化逻辑，导致出现算法运算量大、车辆响应速度缓慢等问题。

在实际情况中，自动驾驶车辆在起步阶段，由于自动驾驶车辆离前车的距离较近时，会导致加速较慢，进而使得从车辆起步到稳定跟车的行驶距离会拉长，会导致自动驾驶车辆无法达到稳定速度。为此，笔者提出了一种新的跟车算法：基于前车车速、距离、当前车速、当前加速度等少量参数，得到最优的期望速度和期望加速度，通过模拟分析对比证明是目前比较适合在自动驾驶车辆实现的算法，优化了算法公式，降低了算法的运算量，提升了车辆的响应速度，实现了快速安全地跟车。同时，基于PID控制提出了一种在跟车算法基础上提升控制精确度的自动驾驶车辆纵向控制策略，通过PID控制计算出一个加速度补偿量，在期望加速度的基础上增加一个补偿量输出给动力系统，提升控制的精度，提升车辆跟车的稳定性、舒适性和安全性。

1 改进的跟车算法

自动驾驶车辆在道路上行驶，遇到前方有车辆时需要先快速、安全地跟随前方车辆，之后再通过决策系统执行换道行驶，因此在跟车过程中需要设定一个策略。笔者引入前方车辆距离权重因子，通过权重计算自动驾驶车辆的期望速度和加速度。在计算期望速度和期望加速度时需要先获得车辆与前方车辆之间的安全距离Ds：

Ds=max{sd,ts*vcurr}

(1)

式中：sd为动态最小安全距离，为系统配置参数；ts为安全时间，为系统配置参数；vcurr为车辆当前车速，通过车辆的轮速传感器进行计算得到。

在获得车辆与前方车辆的安全距离Ds后，还需要获得车辆的变速距离s才可计算车辆的期望速度。变速距离s通过如下的公式计算得到：

s=sf-Ds

(2)

式中：sf为前方车辆距离当前车辆的距离，该值由自动驾驶车辆的感知系统实时输出。

当变速距离s>0时，期望的速度vtar的计算公式为：

vtar=α*vf+(1-α)*vlimit

(3)

式中：vf为前方车辆的速度，通过自动驾驶车辆感知系统实时输出；vlimit为系统设定的最高车速，根据感知系统识别的道路限速标识确定并输出；α为障碍物对最大速度的影响权重，其计算公式如下：

(4)

当变速距离s≤0时，期望的速度vtar的计算公式为：

vtar=min{max(vf-VRC,0),Vlimit}

(5)

式中：VRC为当前车辆在与前方车辆的距离小于安全距离时速度降低值，为系统配置参数。

图1 跟车算法流程图

图2 纵向控制策略

根据输出的期望车速，计算车辆变速所需的时间t：

(6)

根据变速所需的时间t可最终计算出期望的加速度atar为：

(7)

通过算法获得的期望速度vtar和期望加速度atar输出给自动驾驶控制系统；由于计算方法简单以及权重α的存在，可保证在同等安全距离的前提下，加快车辆跟随前车的响应速度，增加系统的反应时间。整个算法的流程图如图1所示。

2 自动驾驶车辆纵向控制策略

为了实现自动驾驶车辆平稳的行驶，需要对车辆的动力系统和制动系统进行协调控制，使得整车在纵向(即整车X方向)上达到决策系统下发的目标速度和目标加速度。

笔者以车辆动力学模型作为前馈环节，计算车辆需求的扭矩；当实际车速与目标车速偏差时，通过PID反馈控制对加速度进行补偿。当车辆需求扭矩为正时，将需求扭矩请求发给动力系统；当车辆需求扭矩为负时，将需求减速度请求发送给制动系统。自动驾驶车辆的控制策略如图2所示。

PID的控制表达式为：

(8)

e(t)=vtar-vcurr

(9)

(10)

(11)

式中：e(t)为系统偏差，在控制系统中为期望速度和实际执行速度的偏差以及期望加速度和实际执行加速度的偏差：Kp为比例系数，根据车辆实际情况进行标定；Ti为积分时间常数；Ki为积分系数，根据车辆实际情况进行标定；Td为微分时间常数；Kd为微分系数，根据车辆实际情况进行标定。

简单来说，PID各矫正环节的作用如下：比例环节及时成比例反映控制系统的偏差信号e(t)，偏差一旦产生，控制器立即产生调节作用，以减少偏差；积分环节主要用于消除静态差，提高系统的误差度，积分作用的强弱取决于积分时间常数Ti，Ti越大，积分作用越弱，反之则越强；微分环节反映偏差信号的变化趋势，即偏差信号的变化速率，并能在偏差信号值变化太大之前在系统中引入一个有效的早期修正信号，从而快速加快系统的动作速度，减少调节时间。

根据计算得到的加速度补偿量acal加上期望的加速度atar获得准确的加速度请求areq发送给车辆的相关执行系统，其计算公式如下所示：

areq=atar+acal

(12)

同时按照车辆行驶方程可以根据需求的加速度反算出动力系统的需求扭矩，车辆行驶方程如下：

(13)

图3 纵向控制系统示意图

式中：Ff为滚动阻力；Fw为空气阻力；Fj为坡度阻力；Fi为加速阻力；r为车轮半径；ig为变速箱传动比；i0为主减速器传动比;ηt为传动系统的机械效率，默认为常值1。

通过计算得到的需求扭矩Treq和需求减速度areq输出给车辆的相关执行器来执行加/减速指令，具体的纵向控制系统输入、输出示意图如图3所示。

3 跟车算法模拟仿真

图4 简单模拟场景

图5 某一段时间内跟车距离曲线

自动驾驶车辆跟车算法性能的评价主要从舒适性(车辆速度、与前车距离的震荡周期)、达到稳定时的时间、达到稳定时行驶的距离、加速度的最大值和最小值、加速度变化率的最大值和最小值、速度的最大值和最小值、安全性(车辆的TTC时间,即本车撞上前车的时间)等几个方面进行考虑。

为验证算法的性能，笔者利用自己编写的简单模拟程序对算法进行了模拟仿真，同时将Li等[7]所采用的跟车算法也进行模拟对比，模拟场景如图4所示。

模拟场景为2车初始位置相距10m，前车为人工驾驶，后车为自动驾驶，设定前车的目标速度为60km/h，后车的目标速度为70km/h。同时前车的加速度为1.51m/s2，减速度为1.01m/s2；后车的最大加速度为1.0m/s2，最大减速度也为1.0m/s2。2车同时开始行驶，行驶200s获取车辆的行驶过程中的数据。提取车辆稳定行驶后某一段时间内(20s)的跟车距离，如图5所示，图5中每帧表示50ms。从舒适性方面来，改进算法的震动频率为0.75Hz，Li算法的震动频率为0.045Hz；改进算法的距离波峰与波谷差异为0.0018m，Li算法的距离波峰与波谷差异为0.0135m。从数据对比可以得出，改进算法相比于Li算法的舒适性略差，但是距离稳定性更好。文献[8,9]的研究表明，震动频率小于1Hz时处于非敏感区，对舒适性影响较小，因此认为改进算法在不影响舒适性前提下提升了跟车距离的稳定性。

根据图6和图7所示，从达到稳定的时间和达到稳定行驶时的距离2个方面来看，改进算法使车辆达到稳定行驶的时间为60.2s，行驶的距离为855.1m；Li算法使车辆达到稳定行驶的时间为62s，行驶的距离为914.6m，性能提升了2.9%，可以看出，改进的跟车算法提升了车辆的响应速度。

图6 车辆速度曲线 图7 行驶距离与主车速度的关系

以2s的距离得到的速度作为采样间隔，提取稳定行驶前的加速度，数据如图8所示，图8中每帧代表50ms。笔者计算得到的加速度最大值为1m/s2，最小值为-0.045m/s2；Li算法的加速度最大值为1m/s2，最小值为-0.0635m/s2。根据自动驾驶车辆的实际测试经验判断，当减速度小于0.3m/s2时，人体的体验较为舒适，因此2种算法的加速度都在舒适范围内，改进算法略好一些。

以2s的距离得到的加速度作为采样间隔，提取稳定行驶前的加速度变化率，数据如图9所示，图9中每帧代表50ms。改进算法的加速度变化率最大值为0.025m/s3，最小值为-0.3178m/s3；Li算法的加速度最大值为0.0167m/s3，最小值为-0.1612m/s3。根据自动驾驶车辆的实际测试经验判断，当加速度的值小于2.5m/s3即为可接受范围，因此2种算法均在可接受范围，改进算法略差于Li算法。

图8 车辆加速度曲线 图9 车辆加速度变化率曲线

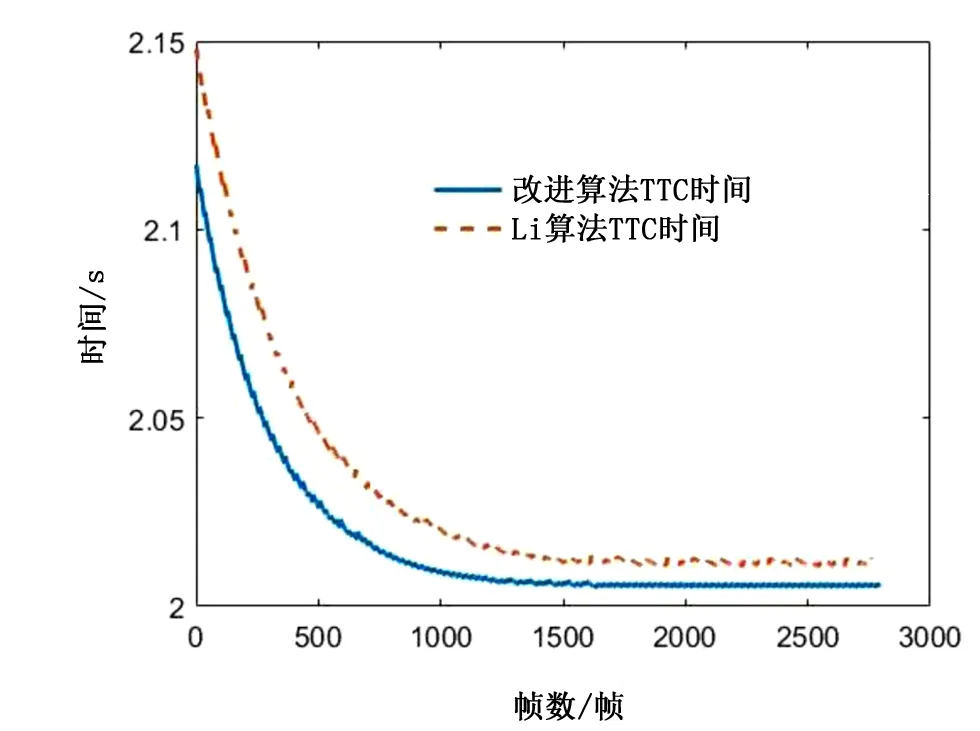
图10 车辆TTC时间曲线

从速度的最大值和最小值方面来看，在跟车稳定后，改进算法的最大速度为60.0255km/h，最小为59.9787km/h，速度波动为0.0468km/h；Li算法的最大速度为60.4919km/h，最小速度为59.9552km/h，速度波动0.5367km/h。根据自动驾驶车辆的实际测试经验判断，当速度波动小于2km/h即为可接受范围，因此2种算法均在可接受范围，改进算法优于Li算法。

从安全性方面来看，在跟车稳定后，提取车辆的TTC时间，其波动情况如图10所示，图10中每帧代表50ms。改进算法的TTC时间最大值为2.1177s，最小值为2.005s，波动值为0.1127s；Li算法的TTC时间最大值为2.1479s，最小值为2.0105s，波动值为0.1374s。2种算法的安全性都很好，改进算法略优于Li算法，性能有小幅的提升，减少了TTC的波动，提升了车辆的安全性。

综合以上各评价因素，改进算法基本优于Li算法，该算法简化了计算公式，降低了算法的计算量，提升了车辆的响应速度，提升了跟车距离的稳定性以及跟车算法的安全性。

4 结论

1)设计了一种结合自动驾驶实际工况的跟车算法，引入距离权重因子和分段计算公式，采用简单有效的算法公式，降低了算法的计算量。

2)建立了基于PID控制的纵向控制策略，引入车辆行驶方程，通过加速度补偿量提升车辆控制精度，实现稳定、舒适、安全地跟车。

3)通过目前的主流仿真软件对算法进行模拟仿真，并与主流算法进行对比分析，全方面分析了改进算法的性能。分析对比结果表明，改进算法提升了车辆的响应速度，提升了跟车距离的稳定性以及跟车算法的安全性。

4)改进算法在车辆接近稳定距离时，偶尔会出现短暂刹车的现象，后续需要对改进算法进行适度的修改，消除减速度的跳变。