基于TOPSIS 法与灰色关联度法的故障样本分配方法

徐 达，焦庆龙

（陆军装甲兵学院兵器与控制系，北京 100072）

0 引言

在装备试验过程中，为了节省试验经费和避免拖延试验进度，装备维修性试验通常是结合可靠性试验来开展的［1］。这样的试验方法虽然能够确保维修性试验验证所需故障样本的真实性，但对于装备的部分子系统来说，在有限的试验期间内所出现的自然故障数量较少，乃至于无故障。因此，这些子系统的故障样本量甚至无法满足基于小子样的维修性验证方法所需的故障样本量要求［2］，这对于全面评定装备是否满足规定的维修性设计要求的程度存在较大困难。

针对上述问题，文献［3］指出可采用模拟故障的方法对故障样本量进行补充，以便达到规定的故障样本量要求。因此，对于模拟故障而言，选取哪些部件，模拟哪些故障，对于维修性试验验证结果的评定具有重要影响。与此同时，文献［3］还提供了两种维修性试验验证故障样本分配方法：按比例分层抽样的故障样本分配法与按比例的简单随机抽样故障样本分配法。这两种方法都是以故障率作为主要影响因素来制定故障样本分配方案，考虑因素比较单一，分配结果不够令人满意。针对这一问题，文献［4-5］分别对故障样本分配所考虑的影响因素进行了扩充，使得故障样本分配结果的可信性与合理性有了明显提高。此外，测试性验证试验中的相近研究工作对于本文的研究具有借鉴意义［6-10］。

针对故障样本分配问题，文献［3-5］皆侧重于考虑故障和部件的相关影响因素，但对于维修作业的相关影响因素考虑较少。然而对于维修性试验验证而言，维修性各指标的核查与验证是通过维修作业来完成的。对此，本文将维修作业的相关影响因素纳入故障样本分配影响因素体系，并提出了一种基于逼近理想解的排序方法（Technique for Order Preference by Similarity to Ideal Solution，TOPSIS）与灰色关联度法的故障样本分配方法，旨在为维修性试验验证提供合理、可行的实施方法。

1 故障样本分配影响因素体系

将故障样本分配的全过程划分为故障产生阶段和故障检测与排除阶段，针对这两个阶段的特点以及综合考虑这两个阶段对于故障样本分配的影响，构建了故障样本分配影响因素体系，如图1 所示。

故障产生阶段是指从模拟故障出现征兆或操作人员启动故障模拟装置时开始，到维修人员进入现场开始进行故障检测与排除时为止的这一时间阶段。该阶段共选取了两个影响因素：故障率和故障模式严酷度。故障率可通过试验期间累积的故障数据获得，或通过威布尔分布函数求得［4］。故障模式严酷度是指所模拟的故障模式产生后，对人员、装备和环境的影响程度［7］。对于故障率越高、故障模式严酷度越高的模拟故障而言，应分配越多的故障样本。

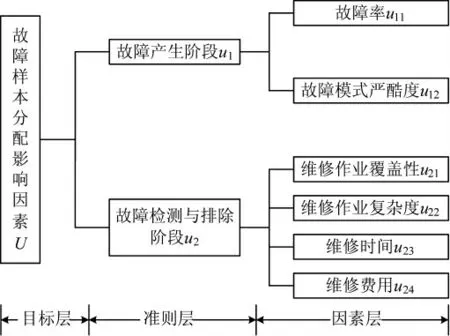
图1 故障样本分配影响因素体系

故障检测与排除阶段是指从维修人员开始对故障进行检测时开始，到故障排除、部件装配与调校完毕的这一时间阶段。该阶段共选取了4 个影响因素：维修作业覆盖性、维修作业复杂度、维修时间和维修费用。维修作业覆盖性是指维修作业对整机的维修性验证情况或结构覆盖情况，维修作业覆盖性越高，表明维修作业过程中涉及的部件数量越多，对整机的维修性验证程度越大。维修作业复杂度是指维修作业的难度，维修作业过程中检测、拆卸和装配等步骤的难度越大，或对维修人员的技术等级要求越高，则维修作业复杂度越高。维修时间（单位：小时）是指故障检测与排除阶段的时间。维修费用（单位：元）是指故障检测与排除阶段所产生的资源消耗、人力消耗等费用的总和。维修作业覆盖性越高、维修作业复杂度越高、维修时间越短、维修费用越少的部件应分配越多的故障样本。

故障模式严酷度、维修作业覆盖性和维修作业复杂度的指标描述及评分等级分别如下页表1～表3 所示。

2 故障样本分配数学模型

2.1 确定影响因素的权重

本文采用主观赋权法中的残缺判断矩阵法［11］对各影响因素进行赋权，以避免出现因影响因素重要度难以比较而导致无法赋权的问题。根据“1-9”重要度标度表（参见文献［11］表5-3）对影响因素间的重要度比较结果进行判断，得到矩阵D：

表1 故障模式严酷度及评分等级

表2 维修作业覆盖性及评分等级

表3 维修作业复杂度及评分等级

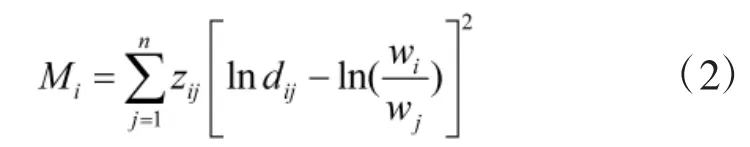
对式（4）进行求解，则可得yi，进而得到影响因素ui的权重：

2.2 数据处理与故障样本分配

TOPSIS 法对方案进行评价的思路是在对规范化的数据进行筛选的基础上，找出最优方案和最差方案，进而根据相对贴近度来评价方案的优劣。但TOPSIS 法的不足之处在于对各方案与理想方案之间关于各影响因素的差别程度区分不够详细。灰色关联度法是根据方案之间的相似度来判定它们的关联程度，是在对每个方案的各影响因素进行比较的基础上给出关联度的。本文将TOPSIS 法与灰色关联度法相融合的方法应用于故障样本分配［12-14］，旨在有效弥补TOPSIS 法的不足，对各部件的影响因素进行综合比较，实现故障样本的合理分配。

首先，建立故障样本分配的原始数值矩阵：

效益型影响因素（即影响因素数值越大，分得的故障样本越多）的规范化处理方法为：

成本型影响因素（即影响因素数值越小，分得的故障样本越多）的规范化处理方法为：

基于上述数据规范化处理方法，得到规范化矩阵：

将权重向量w 与B 相乘，进而得到加权规范化矩阵：

确定各影响因素的正理想解方案X+与负理想解方案X-：

式中：ρ 为分辨系数，ρ∈［0，1］，通常ρ=0.5。

计算第i 个部件与正理想方案、负理想方案的灰色关联度：

分别对所求取的欧式距离和灰色关联度进行规范化处理：

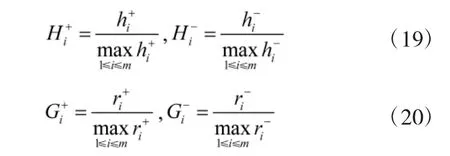
对规范化后的欧氏距离和灰色关联度进行线性加权融合：

计算第i 个部件的相对贴近度（相对贴近度越大，应分得越多的故障样本）：

由此，可得每个部件分得的故障样本数量为：

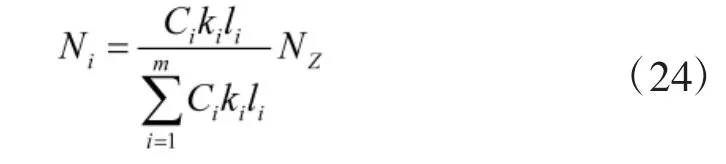
式中：Ni、ki和li分别为第i 个部件所分得的故障样本量、重要度和数量；NZ为故障样本总量。

3 应用实例

以某型装甲车辆的加温器维修性试验为例，该加温器在某型试验阶段所产生的自然故障次数较少（故障率单位：次/10 000 km），鉴于该加温器在该型装甲车辆冬季使用过程中较为重要，订购方和承制方拟对其进行故障模拟，并确定NZ=30，该加温器的故障样本分配原始数据及影响因素权重如表4所示。

令K 和L 分别为：

基于本文所建立的故障样本分配数学模型，并令α=β=0.5，对故障样本分配过程的各参数进行计算。篇幅所限，本文不再给出D，只给出部分参数的计算结果，如所求取的X+、E+和E-分别为：

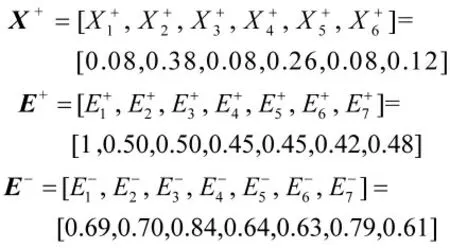
本文所提的故障样本分配方法与按比例分层抽样的故障样本分配方法的故障样本分配结果如表5 所示。

表4 故障样本分配原始数据与影响因素权重

表5 两种方法的故障样本分配结果对比

由表5 可以看出，在对故障样本分配结果进行取整后，本文所提故障样本分配方法与按比例分层抽样的故障样本分配方法的NZ分别为33 和32。但是本文所提方法是在对各部件的影响因素进行逐项比较的基础上，对各部件的优劣程度进行综合排序，并考虑了部件重要度的影响，进而实施的故障样本分配。即故障样本分配结果是在对各部件的影响因素进行综合权衡的基础上进行分配的，所考虑的因素更加全面，分配结果更加合理，在实施上更加切实可行，具有较高的可信度，有效避免了按比例分层抽样故障样本分配方法所致的故障样本分配结果的合理性与可信性不足的问题。

4 结论

本文结合维修性试验验证故障样本分配的工程实践特点，提出了一种基于TOPSIS 法与灰色关联度法的故障样本分配方法。该方法将灰色关联度法引入TOPSIS 法，有效避免了TOPSIS 法在方案排序时维度单一的问题。将欧氏距离与灰色关联度有效融合，实现了在多维空间对各部件的影响因素进行综合比较和排序，使得所制定的故障样本分配方案更加合理、可信，所提方法对于科学、有效地开展装甲装备维修性试验工作具有较高参考价值。