一种基于最优在线无偏估计的空间配准方法*
2019-11-19常超伟王世锋李丽君黄义杰
常超伟,王世锋,李丽君,黄义杰,宋 航
(1.北方自动控制技术研究所,太原 030006;2.山西财经大学金融学院,太原 030006)
0 引言
当代空中监视系统是由能够提供位于传感器公共覆盖区域内的目标数据的传感器网络组成,一个监视系统的目标就是通过从传感器获得的原始数据计算和显示出目标的真实状态。传感器是要融合的数据源,所以数据融合系统成为所有监视系统的一个主要方面。数据融合系统联合传感器探测从而达到比来自于单传感器探测更好的精度和鲁棒性等。
由于传感器上报的量测中包含有随机误差和系统误差部分,随机误差可以使用滤波的方法消除,但是系统误差通过滤波是消除不了的,必须使用传感器配准的方法消除。而在多传感器量测中系统误差的存在不同程度地降低了数据融合系统的性能,例如当多部传感器进行数据融合时,各传感器系统误差的存在可能导致航迹的分裂和误相关,使融合航迹的精度变差,不能最佳地达到多传感器组网的目的。如图1,传感器A 和B 的量测都存在偏差,如果不对其进行估计和补偿,则真实目标就会被融合中心误认为是两个目标,从而导致航迹的分裂。即使融合中心判定两传感器的量测来源于同一目标,融合后的航迹容易出现锯齿效应,如图2 所示。
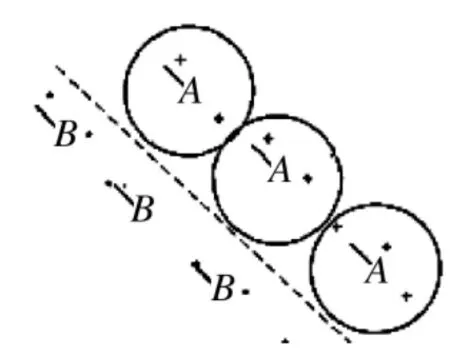
图1 源于单目标的多条航迹
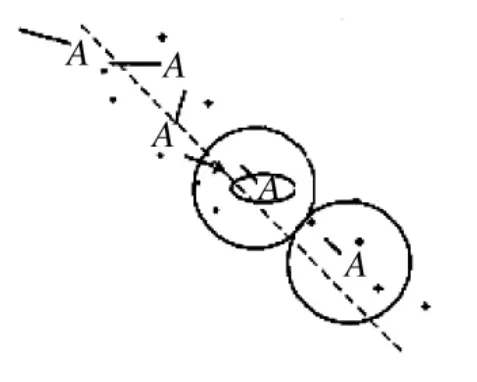
图2 航迹的不稳定性
由上图可见,传感器配准在数据融合系统中是不可避免和必须的。然而系统误差的来源有很多方面,包含距离、方位和俯仰偏差、距离增益误差、传感器定位误差和传感器定姿误差等。一些误差源是静态的并且可以利用试验飞行数据进行离线估计,但是另一些误差源则是时变的。因此,需要使用一种在线的估计方法,当接收到新的量测时更新估计参数,从而保证要融合的多传感器数据一直是无偏的,这种方法就是最优在线无偏估计[1]方法。文献[1]中提出的一种最优在线无偏估计(BLUE)方法是基于二维公共直角坐标系内平移变换的,不能直接在实际工程中应用。鉴于此,本文面向工程应用将该方法从二维场景推广到三维场景,从平移变换推广到基于ECEF(地心直角坐标系)坐标转换的BLUE 方法,然后与最小二乘估计方法、广义最小二乘估计方法进行仿真比较;同时将改进后的方法应用到相对空间配准问题中,对工程应用具有一定的参考价值。
1 基于ECEF 坐标转换的BLUE 方法
1.1 绝对空间配准问题的量测组织结构及算法推导
对于可用数据的处理有几种可能的方法。一种是基于目标航迹和传感器偏差的联合估计,另一种是利用不同传感器探测到的源于同一目标的量测之差。文献[1]中采用的是第2 种方法,它能达到与第1 种相似的性能。
系统实际的输入为量测位置,想要用量测之差来进行估计。问题是,哪一个量测对应该被使用来表示这个作为偏差估计中偏差的差别?图3 用来作为潜在数据组织方法讨论的一个参考。图中的第1行描述了时间线上3 部雷达关于同一目标量测的录取时间。雷达的符号分别为:圆代表雷达1,正方形为雷达2,三角形为雷达3。

图3 量测组织方法
对于估计问题的传统方法是基于偏差估计的独立量测之差的利用。换句话说,一个量测是用作一个并且只用作这个量测之差,避免了包含被算法处理的相关量测之差。这种方法的一个例子如图3(a),只有4 个建立的量测之差。如图3(b)所示,这些数据链包含所有的可用信息,需要注意的是这里有一个相连的量测之差间的相关性:它们共用量测之差中的一个测量,测量中的误差映射到所有的量测之差中。这个主要的差别是考虑到图3(a)中传统的方法,当中一半的可用信息被使用。
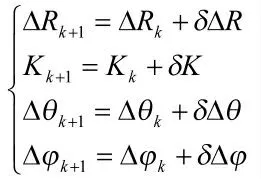
具体算法推导过程如下:

正如在上一部分指出的,量测按时间排列,量测之差通过每一个量测和同一个目标的前一个量测求得:

为了保证一致性,将量测按时间排列是必要的。这个关系表示为:

第i 个下标为每一个量测对之差,εi+1,i为两个量测的联合调整误差。
考虑到包含量测之差的整个向量的协方差矩阵,它直接与每个量测的协方差矩阵Ri有关。
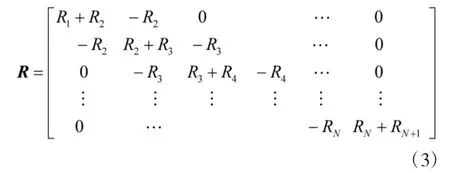
单独的协方差阵Ri是由雷达参数和假定的线性近似得到:
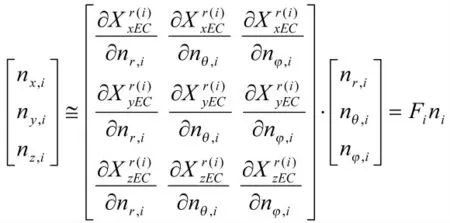
从而

最终,BLUE 估计结果可由以下得到:

最小二乘方法只是没有考虑随机噪声的影响,所以估计公式中没有协方差阵,可将式(4)修改为
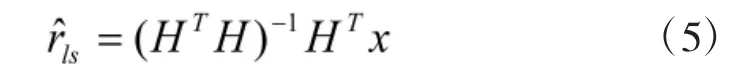
如果将式(4)中的协方差阵R 改为
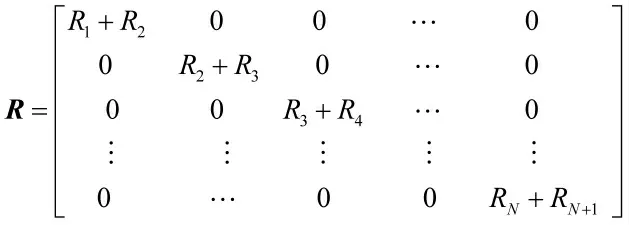
即得到广义最小二乘方法中的估计结果
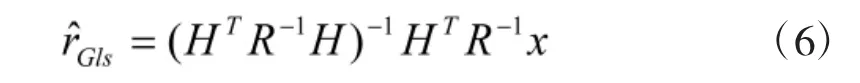
1.2 相对空间配准问题的量测组织结构
上述BLUE 方法适用于多雷达多目标场景下的绝对系统误差估计问题,对传感器分布和目标的数量及分布要求较高,因此,在实际工程应用中受到了一些限制。
在融合系统对雷达探测精度要求不是很高时,采用相对配准的方法来估计各雷达的系统误差以足够满足系统的需求。所以,此时可以设定精度最高的一部雷达作为主站,其他雷达作为从站,对各从站的相对系统误差进行估计。这时图3(b)中的量测组织结构可进行如下改进,如图4 所示,其余算法推导过程和1.1 节中相同。
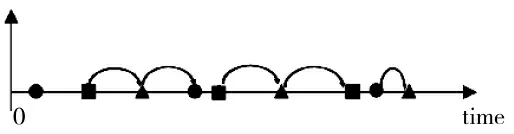
图4 相对配准应用中的量测组织结构
在图4 中,令1 部精度最高的雷达(如雷达3)作为主站,在进行量测处理时,因为只需要估计雷达1、雷达2 相对于雷达3 的系统误差,所以在量测处理上只需要处理雷达1 与雷达3 量测之差、雷达2 与雷达3 量测之差。
2 BLUE 方法与LS/GLS 方法的仿真比较
在第1 部分推导的基于ECEF 坐标转换的空间配准的基础上,使用块处理的思想,对BLUE 方法和最小二乘估计方法、广义最小二乘估计方法在多种场景下进行了仿真比较。
仿真场景为:雷达1 位置(34°,110°,200 m)、系统误差(100 m,0.3°,0.2°)、随机误差(60 m,0.1°,0.1°)、增益误差K1=0.004;雷达2 位置(35°,110°,200 m)、系统误差(-100 m,0.3°,0.2°)、随机误差(60 m,0.1°,0.1°)、增益误差K2=0.005;雷达3 位置(34°,111°,200 m)、系统误差(-10 m,0.05°,0.05°)、随机误差(60 m,0.1°,0.1°)、增益误差K2=0.003。

图5 雷达1 距离误差估计
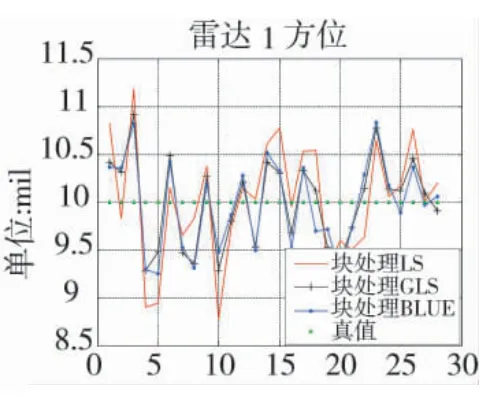
图6 雷达1 方位误差估计
从图5~下页图13 中可以直观地看出,利用BLUE 配准算法进行系统误差估计的结果要优于传统方法(LS)估计的结果。表1~表3 中为3 种方法估计得到的系统误差与误差真值之间的误差均值和方差,BLUE 方法估计误差的均值和方差基本小于LS 和GLS 方法的估计结果,再次从数值上验证了BLUE 方法的性能。

图7 雷达1 俯仰误差估计
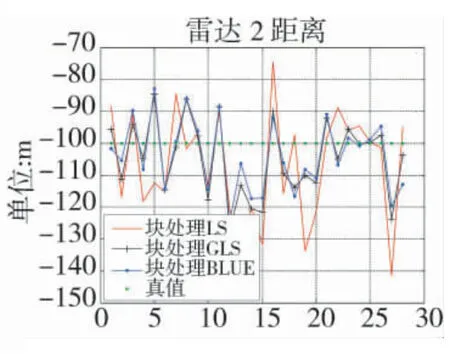
图8 雷达2 距离误差估计

图9 雷达2 方位误差估计
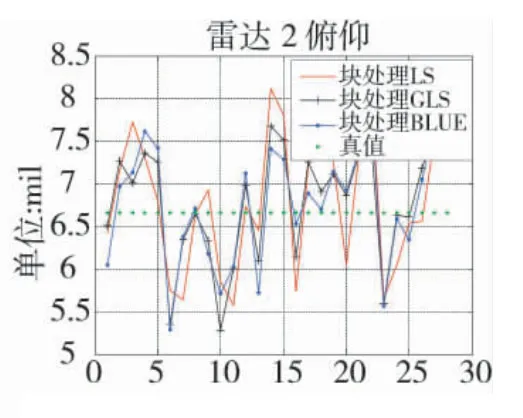
图10 雷达2 俯仰误差估计
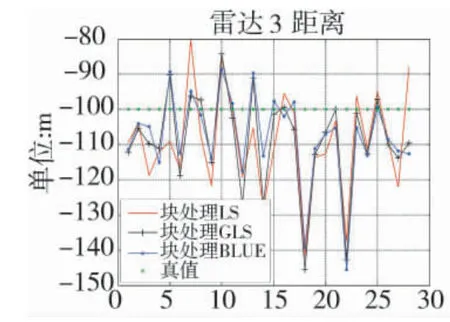
图11 雷达3 距离误差估计

图12 雷达3 方位误差估计
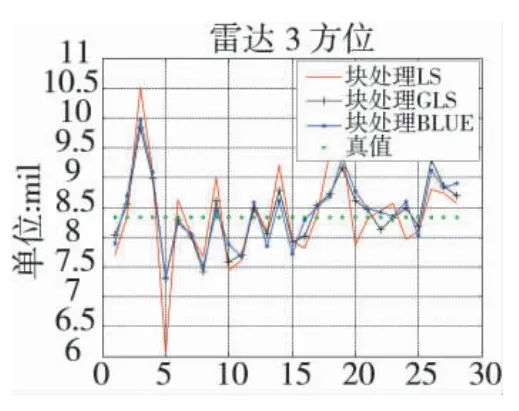
图13 雷达3 俯仰误差估计

表1 各方法估计误差的均值和方差(雷达1)

表2 各方法估计误差的均值和方差(雷达2)

表3 各方法估计误差的均值和方差(雷达3)
3 BLUE 方法在相对空间配准中的应用
在使用1.2 节中相对空间配准问题的量测组织结构的基础上,模拟第2 节中的仿真场景,令雷达3为主站,雷达1 和雷达2 为从站,使用基于ECEF 坐标转换的BLUE 方法估计雷达1、雷达2 的相对系统误差。
从下页图14~图19 中算法估计结果与真值的比较中可以看出,该方法能较好地估计雷达1、雷达2 的相对系统误差,从而证明BLUE 方法不仅能够解决多传感器多目标情况下的绝对配准问题,还能够应用到相对空间配准问题中。
4 结论
空间配准技术是多雷达组网首先考虑解决的关键问题之一,如果配准问题解决不好,则后续的估计、跟踪、识别的精度就会降低。本文对多传感器多目标背景下基于BLUE 方法的空间配准算法进行了研究,在文献[1]中BLUE 方法的基础上,将其推广到基于ECEF 坐标转换的BLUE 方法,并与LS、GLS 方法进行了仿真比较,结果显示出了BLUE 方法的优势。通过修改量测组织结构将基于ECEF 坐标转换的BLUE 方法应用到了相对空间配准问题中,仿真结果验证了算法的正确性。

图14 雷达1 距离误差估计

图15 雷达1 方位误差估计
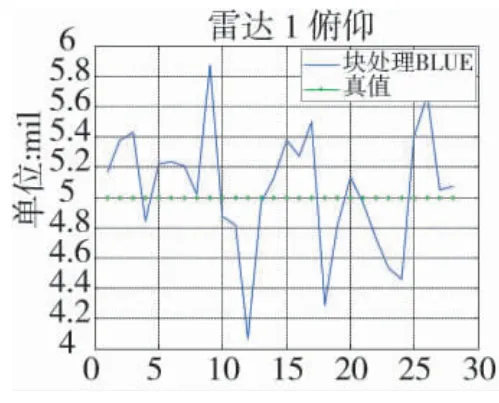
图16 雷达1 俯仰误差估计

图17 雷达2 距离误差估计
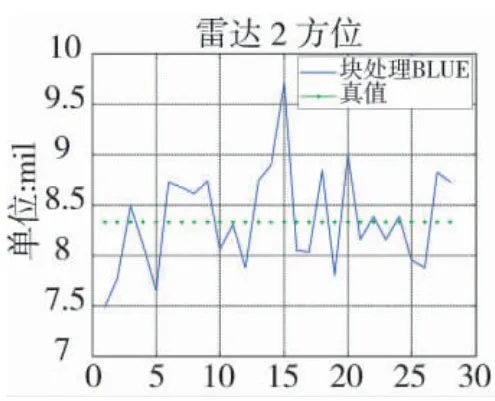
图18 雷达2 方位误差估计

图19 雷达3 俯仰误差估计
