基于BFS 和FPGA-CPU 的混合加速器设计*

郭小波，杨光露

（1.河南工程学院计算机学院，郑州 451191；2.粮食信息处理与控制教育部重点实验室，郑州 450002；3.河南中烟工业有限责任公司南阳卷烟厂，河南 南阳 473007）

0 引言

图作为数据表示和处理图的算法普遍存在于许多科学领域。广度优先搜索（Breadth-First Search，BFS）是研究图的一个关键构建模块，也是各种图指标如计算连接组件、计算图的直径和半径的基础。BFS 以及许多其他图算法的2 个主要特性是由图顶点和边结构上的数据驱动计算引起的不规则的存储访问和较低的计算-存储比［1］。

关于快速图遍历已经提出了一系列研究方法，从采用并行机制的通用CPU 和多核/超级计算方法到图形处理单元（GPUs）、从混合CPU-GPU 方法到利用可重构硬件的方法［2］。最近在现场可编程门阵列（FPGAs）中的多软核处理器上实现了BFS和其他不规则应用的优化［3］；已有研究探索高度并行处理单元（PEs）和解耦计算内存［1，4］，发现小世界网络上的BFS 的执行时间受中间级的控制。文献［1］解耦FPGAs 中的通信和计算单元，以保持不规则存储访问的吞吐量；文献［4］提出了优化BFS，本质上是融合最先的2 个请求响应向量，得到了较少内存需求的改进性能；文献［5-7］提出了在GPU上实现并行的BFS，即在水平同步［5］或定点方法［6］，以及采用高效的缓存数据结构［7］；文献［8］提出在一个4 倍Socket 系统上局部最优化来减少内存流量，并提出采用一个压缩格式（每个节点1 位）的位图来跟踪被访问的节点；文献［9］提出通过一种方向优化方法来减少遍历的边的数量，该方法在父-子和子-父遍历之间切换，它依赖于边沿启发式思想。

近年来，随着人们对节能计算系统的关注，采用可重构逻辑和FPGAs 的异构处理越来越流行，包括采用数据中心［10］；文献［11］提出的CPU-GPU 混合方法采用的是一种切换方法；文献［12］强调了顺序模式对于采用图算法获得高存储设备带宽有明显的优势，并提出了一种采用流分割的以边沿为中心的分散-聚集框架，但这种方法是以牺牲某些效率（如随机访问节点）来实现通用性的图存储，其效率对于BFS 是有限的。

本文通过对BFS 的布尔矩阵向量表示式的观察，提出了一种无失速数据通路的FPGA-CPU 异构处理器的混合BFS 加速器结构，系统采用BFS的冗余工作-带宽权衡算法，把BFS 前沿处理成密集的，以使得冗余计算可换取带宽并提高BFS在混合加速器执行中的性能，总体上更接近硬件角度的思想。

1 背景知识

1.1 广度优先搜索

考虑无向、无加权图G=（V，E），具有|V|个顶点（节点）集V 和|E|个边集E。BFS 从根节点vr开始，vr包含于最大连通分量vr∈Vc，Vc⊂V，而且遍历相邻vj的每条边erj，这样，图就是按级遍历的，每级的全部节点在下一级处理之前都被搜索。与其他研究搜索BFS 性能［1，4，11］的算法一样，本文考虑得到距离数组的关键变量，即dist，它是根据BFS 步骤得到的每个被访问节点与根节点的距离。

1.2 稀疏性与小世界特性

一个小世界图就是一个直径很小的图，如“六度分离”，而对于社会图如脸谱网来说，已被证明低至四度。小世界图一般表现为无标度分布形式y=xa，即由极少数高度中心“枢纽”和形成外围的许多低度节点构成。这意味着当BFS 开始时，存在根节点仅被连接到几个相邻节点的一个高概率，而且那些相邻节点连接到少数节点，等等。因此，BFS 的第一次迭代访问一小部分图。但随着越来越多的边被遍历，前沿规模急剧增大，就构成了很大的网络。

2 基于BFS 和FPGA-CPU 的加速器

2.1 采用线性代数语言的BFS

本文采用“半环上矩阵”的概念［13］把BFS 表示为一个线性代数运算。核心思想是用线性代数来代替数字数据类型以及乘法和加法算子，把各种算法表示为矩阵-向量运算。

具体来说，就是在布尔半环上利用矩阵乘向量运算来实现BFS。在实际中，这个运算“乘以”一个二进制矩阵和一个二进制向量，分别用布尔与（AND）和或（OR）运算代替正规的乘法和加法运算。为了避免与实数上正规的矩阵-向量“相乘”相混淆，这里用“⊗”表示“相乘”运算符。每个yt=A⊗xt运算对应一个广度优先步骤，而且每个结果向量yt是步骤t后图中被访问节点的表示。矩阵A 是图的邻接矩阵，同时初始输入向量x0被初始化为全零，除了在根节点位置上的1 外。结果向量yt作为下一步的输入向量xt+1，这反过来在它的结果向量中又得到更多的访问节点，直至结果收敛。

2.2 解耦距离生成及布尔BFS 算法实现

在2.1 节中给出的BFS 布尔环矩阵-向量表示在存储需求方面是非常简洁的，这使得它适合于硬件加速器的实现。具体来说，对于每个图节点，x 和y向量仅需要1 位存储。由于矩阵稀疏性，y 将被随机访问，保持被随机访问数据的范围和容量最小，对于性能是有利的。遗憾的是，迭代调用⊗对于BFS是不够的，因为它只生成被访问节点的状态而不是dist 数组。

为此，通过在每个⊗调用之后，引入一个单独的距离生成（DistGen）步骤来解决这个问题。如果一个节点i 在BFS 步骤t 的过程中被访问，则它有距离t，而且我们知道，一个节点不能从被访问到不被访问。因此，如果该节点在xt中未被访问，而在yt中被访问，则它有距离t，或dist［i］=t⇔（xt［i］==0∧yt［i］==1）。为了得到距离信息，在每一步骤完成后，必须检查每个BFS 步骤的输入和输出向量。这个数组比较操作来自于正规BFS 步骤被解耦，而且可以很容易并行化或用硬件实现来降低其性能开销。采用⊗和DistGen 的完整BFS 算法实现如算法1。

算法1 采用⊗和DistGen 的BFS 算法伪代码

2.3 带宽和冗余计算之间的权衡

由于稀疏图的遍历涉及很少的实际计算，而且被视为是一个内存约束问题，故用高带宽传送图数据对于加速器性能来说是至关重要的。因此，对于设计BFS 硬件加速器来说，存储访问模式的分析是一个关键步骤。在本文设计的加速器中，BFS 的输入存储在动态随机存取存储器中，而且访问也从DRAM 中进行。

前文分析表明，输入向量xt可以被处理为稀疏来避免冗余工作。但线性代数符号告诉我们，又可以把xt处理为密集的，而且仍然得到正确的BFS 结果。在一个混合加速器中，把BFS 输入前沿处理为密集的看似非正常的想法和执行冗余工作对整体性能来说实际上是有利的，因为有更简单的DRAM访问模式。如何处理xt向量直接影响矩阵A 的数据将如何被访问，反过来说，就是使用多少带宽。

图1 描述了把xt处理为稀疏如何影响矩阵数据的内存请求。加速器必须首先获得一个节点索引，这个索引是通过读dist 的前沿的一个成员，然后得到这个节点的开始和结束指针，并最终使用这些指针获得相邻边的列表。可见，当前的请求依赖于对先前请求的响应，这是典型的间接访问应用，而且xt的稀疏处理导致二级间接寻址。首先是请求速率受响应速率的限制，其次是elems 数组的读脉冲的长度受节点中边数量的限制，最后，虽然读elems数组是按次序的，但在使用的数组部分之间可能存在较大的差距，因为前沿节点离得更远，导致部分DRAM 行缓冲区不被使用；相反，如果把xt视为密集的，并考虑图的每个节点，则A 的访问模式变得非常简单。特别地，可以简单地读出整个矩阵，即可以采用最大长度脉冲读操作来完成，而无需等待来自先前请求的响应。这对于获得高DRAM 带宽来说，是一种更简单和更合适的访问模式；通过把xt视为密集的所要做的冗余工作的数量与前沿有关，前沿越小，要做的冗余工作越多。然而，由于本文构建的是一种混合CPU-FPGA 系统，加速器能处理大前沿的BFS 步骤，故冗余工作的开销就不重要了。

图1 稀疏xt 的内存请求结构

2.4 处理单元结构

基于2.1、2.2 和2.3 的思想，现在来描述BFS 的硬件结构。为了比较2.3 所描述的稀疏和密集xt处理的效果，考虑2 个处理单元（PE）变量。

1）密集x 变量：密集xt处理单元的体系结构如下页图2 所示。该体系结构以数据流方式组织，并模块化成3 个主要组成部分：一个后端，它通过系统互连到DRAM，一个前端，用于执行⊗运算，以及一个距离生成器。后端负责与主存储器的全部交互，包括读出矩阵和向量数据，并写入更新到距离向量。矩阵和向量数据由后端请求并提供给前端使用，前端执行BFS 步骤操作并更新结果向量存储器。具体来说，每当输入向量为1 时，前端仅写1 s结果到由边显示的存储地址。边计数数据用于确定何时读取新的输入向量元素。一个为0 的输入向量值意味着边来自于一个还未被访问过的节点，而且这个数据被简单地丢弃而无需进一步运算。加速器的控制和状态接口通过内存映射寄存器提供。

图2 密集xt 处理单元的体系结构

2）稀疏x 变量：根据整体架构，稀疏xt变量与密集xt变量是相同的，除了它不需要输入向量FIFO（因为稀疏处理意味着全部xt值是1）部分。图3 所示为稀疏xt后端的内部结构，与密集xt变量本质上是不同的。稀疏输入向量是通过前沿滤波器内部生成，它扫描距离数组的值，并发送索引值，全部值被写入在先前的BFS 步骤中。之后，每个生成索引的开始和结束指针被请求，这两个指针用于请求该节点的边数据，并生成前端的边计数信息。

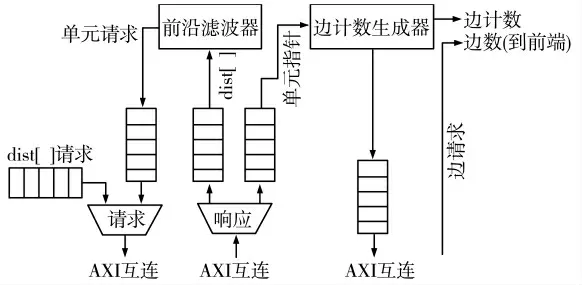
图3 稀疏xt 变量的后端结构

3）失速y 写入：为了保持加速器运行而无停顿，前端能够如后端生成数据一样快地消耗数据是很重要的，因此，可以抽取出前端的功能作为处理一个流写入到随机地址。如果结果向量被存储在DRAM 中，则连接的写请求缓存器和存储控制器可能填满并暂停整个加速器。为了避免这种情况，解决方案是利用向量表示的稀疏性。由于本文的方法要求仅保留每个图节点的1 位，故可以有效地利用片上RAM 的双端口FPGA，在每个周期提供2 个非常快的随机访问。

4）距离生成器：在每个BFS 步骤完成后，调用距离生成器来执行DistGen。这涉及到比较输入和结果向量，并找到从未被访问过的节点到访问过的节点。这些节点的索引被传递给后端作为实际写当前BFS 距离到对应的存储位置，并为密集变量的下一个BFS 步骤更新x 向量。

2.5 一个实际加速器系统的构建

本文构建的加速器系统采用Xilinx Zynq Z7020 FPGA-CPU 混合结构，部署在ZedBoard 平台上［14］；加速器组件首先采用Chisel［15］构建，然后采用Verilog 后端生成Verilog 描述，并导入到Vivado 中作为IP 模块；随后采用Vivado IP 集成器（2014.4 版）来构建加速器系统，包括Xilinx 提供的IP 模块作为结果存储模块RAM（BRAM）和AXI 的互连。64 位AXI高性能（HP）从端口可利用DRAM 带宽的约80%（3.2 GB/s），用于提供数据给加速器；构建中还需要考虑并行性和速率平衡的实现，以及软件BFS 的实现和FPGA-CPU 切换。前者采用并行PEs 来搜索图，并采用FPGA 稀疏矩阵-向量乘法速率平衡思想［16］来估计平台上需要消耗可用DRAM 带宽的PE 数量。后者通过加入一个简单的硬件加速器来保持来自于切换的性能开销达到最小化。至于方法切换，在每个BFS 步骤完成后，软件使用一个简单的模型来决定下一步应该使用哪一种方法。BFS 开始执行软件，当预测的BFS 步长时间对于FPGA 更短时，就切换到FPGA 执行。利用密集变量的可预测性来建模它的执行时钟周期如下：

式中，β 是利用的带宽部分。FPGA 继续执行直至前沿尺寸下降到低于全部图节点的θ%。之后，软件BFS 接管直到搜索终止。β，θ 凭经验确定。

3 实验结果

为了评价本文提出的加速器系统，采用Graph500 基准参数（A=0.57，B=0.19，C=0.19）［1，4］综合生成的RMAT 图，把一个具有规模S（2S个节点）和边因子E（E×2s 条边）的RMAT 图称为RMATS-E。

3.1 软件BFS 和基于BFS 的稀疏和密集变量加速器性能比较

图4 RMAT-19-32 上加速器和软件BFS 每步执行时间

先比较基于BFS 的稀疏和密集变量加速器与BFS 软件算法的性能。对于2 种加速器变量，在有相等数目（4）的PE 和时钟频率（100 MHz）的RMAT-19-32 上执行BFS，得到的每个BFS 步骤（包括距离生成）所花的时钟周期数如图4 所示。从图4 可以看到，步骤1 和2 采用CPU 即软件BFS 搜索，步骤3 和4 切换到密集x 加速器，步骤5 和步骤6 又切换回到CPU，从而实现最快执行；密集变量加速器优于稀疏意味着从DRAM 带宽增加带来的好处要大于中间步骤冗余数据获取的代价。

为了更好地理解为什么密集变量加速器在大前沿的步骤过程中优于稀疏变量加速器，实验得到了对于BFS 的步骤3 和4 的2 种变量加速器的总的读带宽利用率，如图5 所示。对于稀疏变量加速器，实际上观察到在步骤4 中，特别低的带宽利用率是由比步骤3 更大的前沿引起的，导致并行PE请求全部边数组，从而导致许多DRAM 内存冲突和行缓冲失误；另一方面，密集变量加速器的带宽利用率远远高于稀疏变量加速器，在4 个PE 时峰值达到78%，而且在2 步之间没有变化。

从图4、图5 可见，采用BFS 算法的软件解决方案对于开始和结束是最好的，密集变量加速器对于中间步骤总是优于稀疏变量加速器。因此，在下面的性能评价中将省去稀疏变量加速器的结果。

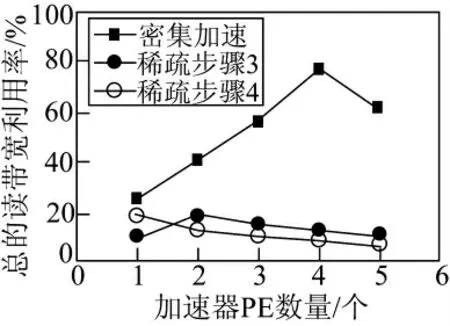
图5 RMAT-19-32 的步骤3 和4 的总读带宽利用率比较

3.2 单一方法和混合BFS 的性能比较

现在来比较在一个RMAT 图上仅采用BFS 软件算法、仅采用密集变量前沿加速器和混合BFS 方案的性能。根据经验取β=0.78 和θ=5%来执行接近理想的切换。性能指标采用每秒遍历边的百万条数（MTEPS），结果是对16 个BFS 操作求平均值。

图6 所示为得到的关于一系列RMAT 图的3种方法的性能与图的规模-边因子的关系。可见，仅采用BFS 软件算法有一个22 MTEPS 的平均性能。由于这些图都不适合CPU 的高速缓存，故大量的数据高速缓存未被使用，降低了性能；而仅采用密集变量前沿加速器是仅采用BFS 软件算法的3.9倍。这是由于CPU 的频率优势和大量冗余数据量获取以及通过加速器执行运算，这种加速进一步支持了慢时钟，而且并行FPGA 加速器适合于不规则的、内存受限的应用；最后，混合BFS 方案结合了二者的优势，所以优于仅采用加速器和仅采用软件的BFS，分别是它们的2 倍和7.8 倍的加速性能。

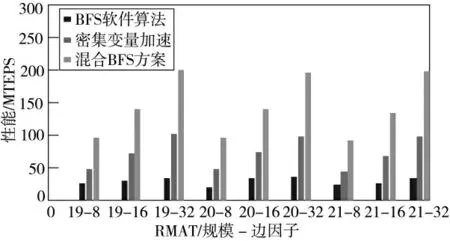
图6 RMAT 系列图上的性能比较

3.3 不同算法的性能比较

由于算法的性能随着更多的带宽可用而成比例增加，故在不同硬件平台上关于相同RMAT 图的搜索比较就不能采用MTEPS 性能指标，所以采用每单位带宽的遍历数作为性能指标，即用MTEPS 遍历速度除以各自的外部存储器带宽（GB/s）来得到。表1 所示为得到的采用本文的密集变量BFS 算法与目前比较先进的混合BFS 算法［1，4，11］的性能结果。从表1 可见，本文所采用的密集变量BFS 算法相比于其中最好的解决方案［4］，在有效每带宽遍历数方面也是其2 倍以上。

表1 不同混合BFS 算法的性能比较

4 结论

本文针对FPGA-CPU 混合硬件系统提出了一种加速的BFS 体系结构，它可以有效利用小世界图中不同程度的并行性，把BFS 视为在布尔环上的一个矩阵-向量运算，把输入向量处理为密集，使得能够在冗余计算和增加DRAM 带宽之间进行交换；在ZedBoard 平台上的实验结果表明，本文提出的混合系统加速器性能能够随着增加的带宽按比例提高，而且在每带宽遍历数性能方面优于其他的技术。