应用多种高精度测量机制的电参量分析仪研制
2019-11-18曾舒帆张绍旺李亚娟饶杰何洪伟牛跃宏
曾舒帆 张绍旺 李亚娟 饶杰 何洪伟 牛跃宏

摘要:針对计量测试过程中高精度电参量分析的需求,该文提出多种改善分析测量精度的测量机制,包括高精度交流电压采样分压器、高精度改进型双级交流电流互感器、利用DDS实现准同步采样原理进行信号频率跟踪实现同步采样以及非整周期傅里叶补偿谐波算法。并将这些测量方法应用到分析仪的研制设计中,实现电参数测试准确度优于0.01、谐波分析准确度优于0.02%的高精度电参量分析仪。
关键词:电参量分析;m-n型同轴电压分压器;非整周期傅立叶补偿算法;同步采样
中图分类号:TP391 文献标志码:A 文章编号:1674-5124(2019)09-0094-06
0 引言
目前国内计量技术机构、电力部门对高精度、多功能的电学参数分析技术和产品有需求。国内研究人员更多的是进行功率测量仪[1]或谐波分析方法[2]的研究。文献[3]在多功能电参量分析仪研制中提出过多功能电参量分析仪的设计思路和方法,但未提及高精度设计的方案。朱自科[4]提出基于DSP的电参数测量仪研制,文中仅对基于DSP和
收稿日期:2019-01-08;收到修改稿日期:2019-03-30
基金项目:国家质检公益性行业专项(201410133)
作者简介:曾舒帆(1982-),男,云南昆明市人,高级工程师,硕士,主要从事电学计量科研工作。AD采样技术的研制方法进行了阐述,并且该文未提及波形分析算法和提高精度的方案。王磊[5]在新型闪变分析仪标准装置的研制过程中提出过高精度m-n型同轴分压器在电压采样中的测量设计方案。陆祖良[6-8]提出在周期信号采样分析过程中的采样策略以及非整周期采样工频谐波分析仪的研究方法。本文在之前的研究基础上通过对分析仪各个关键环节测试精度的改善,设计测试准确度优于0.01%的高精度分析仪。
1 分析仪硬件结构
分析仪结构如图1所示,电压信号通过分压器电流信号通过互感器经过可控放大器进入AD变换器采样成为数字信号后由DSP进行分析和计算,图中深色部分为本文研究内容:设计m-n型同轴等电位屏蔽分压器提高电压采样精度;设计改进型双级电流互感器提高电流采样的精度;设计基于DDS的同步采样电路降低非同步误差;设计频率跟踪算法和非整周期傅里叶补偿算法提高分析准确度。
2 电压分压器的高精度设计
电压采样器设计为高精度电阻性分压器,为了降低外部环境对被测电压信号的影响,首先设计了鼠笼同轴结构的低电位屏蔽机制,如图2所示,可有效屏蔽外部干扰信号对测量信号的影响,但是同时在每个电阻端点都存在着对地的泄露电容造成电压输出端信号与被测信号之间的相位偏移。
通过二次电压V反映输入电压Vin,需要通过电压电阻以及泄露电容的相互关系计算出V与Vin的理论关系
由式(1)可计算出V与Vin间的角度差为
由于R2≥R,而且很小,
所以θ1≈-ωRC,由于R1-R2相同的算法可以求出V与Vin的角度差为
θ≈-ωRC-ωR1C2/2-ωR1C1/2(3)
可以看出低电位屏蔽的电阻性分压器容性泄露造成的相位误差由泄露电容引起,通过计算几何尺寸可以估算出泄露电容值在50Hz时造成的角度偏差为30μrad,在功率测量中弓}起的综合误差为0.004%;在2.5kHz的时候造成的角度偏差为1.5mrad,在功率测量中引起的综合误差为0.03%。对50次谐波电压进行分析时角度偏差引起的综合误差达0.1%。
为降低这项误差,设计图3所示等电位屏蔽结构,在与地屏蔽辐条结构的对称位置上安装同样尺寸的金属条幅并连接Vin,使用高电位端对地泄露电容进行补偿,消除电压信号对地泄露造成的误差。补偿后,在2.5kHz点,上述角度偏差降至10μrad,在功率测量中引起的综合误差为0.004%,50次电压谐波分析误差降至0.01%。
另外为了消除采样电阻自身寄生电容带来的误差,设计了M只电阻串联和N只电阻并联结构,由于每一只电阻自身的寄生电容大致相同MN共同对分压比影响的总作用可以忽略,分压器的输出输入比为1/(MN+1)。
本文对3种设计结构的电阻分压器在标准源380V、2.5kHz输入信号条件下进行了二次输出与等效模拟电流信号积分测试,分别在不同相位、频率条件及电压百分比条件下测试并计算出模拟功率测试最大误差,结果如表1所示。按照m-n型等电位屏蔽同轴结构设计的电阻分压器在工频测量条件下幅值误差优于0.004%,相角偏移量小于10μrad。
3 电流互感器的高精度设计
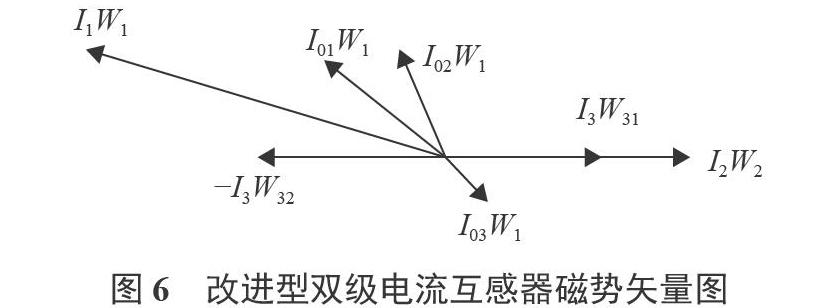
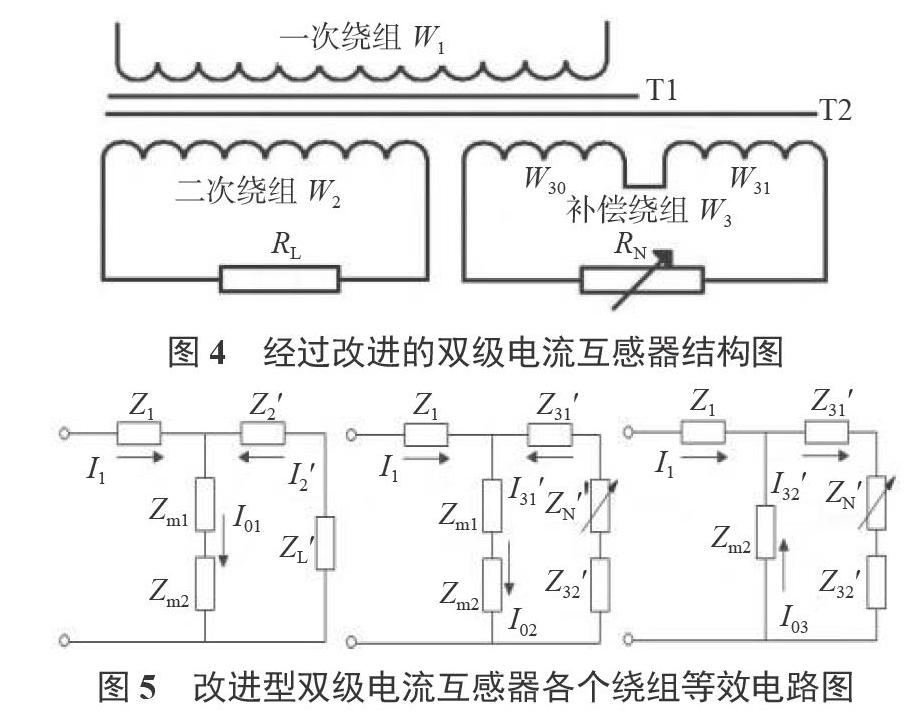
采用电流互感器进行电流采样,电流互感器的误差取决于互感器的励磁电流,互感器二次电流与一次电流的误差正比于激磁阻抗上流过的电流。在采样后的运算中互感器引入的比差可以很容易通过算法进行修正,但是角差很难通过算法进行修正,所以应当尽量减小互感器传递过程中角差的影响。为补偿传递过程中的误差,本文设计如图4所示的带补偿绕组的双级电流互感器,图中一次绕组W1和二次绕组W2以及补偿绕组的一部分W30同时绕在铁芯T1及T2上补偿绕组的另一部分W31反向绕在铁芯T2上且只与T2相交链。
绕组W2、W30、W31的等效电路分别如图5所示,由图中等效电流知铁芯T1的磁势方程为:
I1W1+I2W2十I3W31=(I01+I02)W1(4)
铁芯T2的磁势方程为:
I1W1+I2W2-I3W32=(I01+I02-I03)W1(5)
I1为一次绕组电流,W1为一次绕组匝数,I2为二次绕组电流,W2为二次绕组匝数,I3为三次绕组电流,W30为三次绕组正相绕制并同时与T1、T2相交链绕组匝数,W31为三次绕组反向绕制且仅与T2交链绕组匝数,I01、I02、I03分别为3个绕组作用在铁芯上的激磁电流。由于W31反向绕制因此在磁势方程中的符号为负。
磁势方程矢量图如图6所示。从图5和图6可以知道,改变补偿绕组负载RN将会同时影响I3和I03的大小,当W31与W32相等时,从向量图可以看出I3的大小不会对I1与I2造成影响,增加RN则I03的实部减少同时其模增大,改变103的大小对改变互感器角差的影响远大于对角差的影响,由向量图可以分析得出当向量I03W1能够最大限度抵消I0W1与I02W31的向量和时,I1与I2的误差最小。
应用本文所述的方法其关键在于设计稳定度高温度系数小的电阻作为采样电阻以及补偿绕组负载。对于RL的要求是数值稳定精确且稳定性高温度系数小,因此本文采用高精度金属箔电阻作为采样电阻。对应RN的要求是稳定度高温度系数小且易于调节其数值,因此采用锰铜丝作为材料的线绕电阻作为补偿绕组负载电阻,可以通过增加或者减少绕组数量进行数值调整,通过并联数值远大于线绕电阻的精密电阻进行微调。改进补偿结构的双级电流互感器以及补偿绕组线绕电阻如图7所示。
本文对3种设计结构的电流互感器在标准源50Hz、100A输入信号条件下进行了二次输出与电压信号积分测试,分别在不同相位条件及电流百分比条件下测试并计算出模拟功率测试最大误差,结果如表2所示,改进型双级结构设计的电流互感器在工频测量条件下其整体测量误差优于0.005%。
4 同步采样电路设计
前文已经通过改进采样机制提高了电压电流测量准确度,要提高功率测量的准确度还需要改善电压电流采样同步性的问题。采样信号的功率以及功率相关运算(功率因数、相位差、电能)都是基于对电压电流离散采样点U[n]和I[n]的累加积分运算,计算中电压电流信号如果不同步会出现图8所示的结果,原本同相的点运算后出现图示相位误差。
在对电压电流波形进行谐波分析时需要应用到傅里叶变换(DFT),而理想的傅里叶变换是对无限长序列周期信号进行的,但是在实际分析过程中无法进实现如此大的运算量,因此必须对周期信号进行截断,如果采样频率不是被测信号频率整数倍(不同步采样)就会造成截断效应和频谱泄漏,造成转换到频域的信号失真造成分析误差。
本文设计了如图9所示的采样电路。电路的核心器件是18位逐次逼近型模数转换器,使用直接数字频率合成器AD9850实现采样频率跟踪电路,通过频率跟踪算法计算出信号频率,直接合成信号频率整数倍的采样脉冲驱动AD工作,这样就可以基本消除图8所示的不同步采样误差以及初步降低DFT截断效应和频谱泄漏带来的分析误差,为改进算法提供更好的补偿条件。
5 频率跟踪算法
过零算法跟踪信号频率。初始设置采样频率为fs,选取如图10所示两个信号周期中的正过零点n1、n1';负过零点n3、n3';波峰点n2,n2'以及波谷点n4、n4'。
各点的幅值分别为A1、A1'、A2、A2'、A3、A3'、A4、A4',分别计算同一周期点的幅值差绝对值|Ai'-Ai|以及时间差n'-n。图11为频率跟踪算法流程图,设置阈值X、次数值C。
判断所有4个点是否满足|Ai'-Ai|
6 非整周期傅里叶补偿算法
本文在用上文方法实现准正周期采样的基础上应用了补偿算法对运算结果进行补偿实现非整周期信号的准确计算。
可以用式子(n+△)h=2πm来描述采样的不同情况。这里h是采样的间隔,n是m个周期内的采样个数。△是与n一样,是无量纲的量,对应于n称为采样个数,△可以称之为“整周期采样的补数”。上文中已经使用采样频率跟踪,实现了准整周期采样将|△|控制在1以内,方便进行下一步补偿。假定周期信号为:y(x)=a0+aksin(kx)+bkcos(kx)其中宗量x=2πt/τ,τ是信号周期或基波周期,k是谐波的阶次,其上限是w。其傅立叶系数记为2w+1维列向量
a=(a0,a1,a2,…,aw,b1,b2,…,b)T(6)
但通过上述实际的DFT运算,获得的结果为a,它同样为2w+1维列向量,
a=(a0,a1,a2,…,aw,b1,b2,…,bw)T(7)
这里aT表示a的转置向量为了由a获得a,可由下式计算a=FR-1a,FR为2w+1维矩阵矩阵F由ak和βk构成,ak和βk由不同的积分近似算法决定,F的逆矩阵可以计算得到;而a已经从采样数据经过DFT获得,△由采样点直接计算得到:
△=(S0+S1+Sn+Sn+1)/(Sn-S0+Sn+1+S1)(8)
S代表下标对应采样点的数值,因此所需要的向量a可以计算得到。根据此算法对非整周期信号采样作用是明显的,当补数△位于0.05附近时,补偿效果达到3个数量级,补偿后剩余的误差,达到10-7数量级。
为试验其所具有的能力,作模拟试验分别用一般的DFT算法和本文提出的补偿算法,从同一采样数据列中计算出幅值,比较与设定值接近的程度。试验中离散信号一个周期内的采样数据约60个。两种方法都使用了一个周期的采样数据进行计算。表3是模拟试验的结果。
由实验结果可以看出,当补数△位于0.05附近时,补偿效果达到3个数量级。在实际测量过程中可以通过频率跟踪将△控制在0.5以内,补偿后剩余的误差,达到10-5数量级。
7 整机测试和分析
使用Radian 0.01级电能标准表以及6100B电能质量分析仪作为参考进行测试。对功率准确度以及电压电流谐波分析进行了综合测试。
分别对分析仪的电流、电压的准确度进行了测试,表4为三相中误差最大的一相的测量结果,从结果可以看出最大误差值均优于0.01%,测量结果具有较好的线性度。
对分析仪的功率在不同负载条件下进行了测试,表5为三相中误差最大的一相的测量结果,功率测试结果满度量程:220V,10A,从测量结果可以看出在不同的负载条件下最大误差值為0.0097%,优于0.01,且具有较好的线性度。
进行电压电流在不同次数谐波含量下进行谐波分析,表6中选取了三相中误差最大的一相的结果,谐波分析误差测试,电压基波220V,电流基波10A,各次谐波含量5%,从结果中可以看出谐波分析误差优于0.02%基波幅值。
8 结束语
本文给出了采用多种措施高精度电参量电参量分析仪研制方法,在综合硬件及软件设计方法的基础上分析仪准确度达到较高水平,经过测试研制的分析仪电压、电流、功率、谐波测量准确度均优于0.02%,电压、电流谐波分析准确度优于0.02%,并且开发成本较同类国外设备低,有较高性价比。本文所述设备通过采取一系列手段控制各个环节的测试误差提高了分析仪的整体测试精度,经测试满足高精度分析仪需求。
参考文献
[1]张树.高精度功率分析仪的校准与参数计算研究与实现[D].成都:电子科技大学,2018.
[2]王凯思源.高频电能信号谐波分析算法的研究[D].哈尔滨:哈尔滨工业大学,2018.
[3]曾舒帆.多功能电参量分析仪的研制[D].昆明:昆明理工大学,2011.
[4]朱自科,李亚娟.基于DSP的多功能电参量测试仪的研制[J].昆明理工大学学报,2005(10):227-229.
[5]WANG L,ZENG S F,ZHANG J T,et al.A new flicker teststandard based on asynchronous sampling technology andcompensation algorithm[J].CPEM,2010:331-333.
[6]陆祖良.周期信号采样测量策略[J].电测与仪表,2008,45(10):1-6.
[7]陆祖良.通过采样测量技术建立相角基准[J].计量学报,2007,28(1):1-4.
[8]陆祖良.非整周期采样和工频谐波分析标准研究[D].北京:清华大学,1991.
(编辑:刘杨)
