基于空气耦合超声导波法对开闭器水层厚度的研究

常俊杰 曾雪峰

摘要：针对传统接触式超声检测高压电线杆开闭器水层厚度存在漏电风险问题，提出使用非接触式空气耦合超声导波技术对开闭器中水层厚度进行测量。对开闭器水中导波传播过程进行仿真并计算水层厚度;搭建开闭器实验室平台，控制水层厚度，改变换能器之间距离，对回波信号进行分析并计算水层厚度;控制换能器之间距离，改变水层厚度，对回波信号进行分析并计算水层厚度。通过仿真与实验使用几何声学对水层厚度进行计算得出关系式，将仿真与实验两者结果进行对比，有高度一致性，验证空气耦合超声导波法对开闭器中水层厚度测量的可行性与准确性。该方法可为测量开闭器中水层厚度提供新思路。

关键词：空气耦合超声;导波;开闭器;水层厚度

中图分类号：TG115.28 文献标志码：A 文章编号：1674-5124（2019）09-0027-06

收稿日期：2018-11-14;收到修改稿日期：2018-12-12

基金项目：国家自然科学基金资助项目（11464030）;无损检测技术教育部重点实验室（南昌航空大学）开放基金课题（F010404）

作者简介：常俊杰（1964-），辽宁大连市人，副教授，博士，主要从事超声无损检测的应用技术研究及检测设备的研发等工作。

0 引言

目前，为保证电力系统高效运作，以及在某个区域发生断电事故时，能够快速向电路完好的区域通电，会在电线杆上设置柱上开闭器，其作用是控制向下一个区域输入和切断电力。柱上开闭器在长期使用过程中，由于密封圈老化和外箱腐蚀，箱内会浸人雨水，绝缘性降低，从而可能导致停电等电力事故。有研究通过使用接触式超声波探头接触开闭器底部，观察水面的反射波来检测当前水层厚度。但是，由于这种逐一接触检测需要直接接触底部，可能会在接触时和连接检测仪时产生震动使内部水面摇晃，导致水进入内部机械部分从而发生内部短路，由于开闭器外箱和检测装置相连，万一内部已经短路，则会危及检测人员生命安全。

因接触式超声检测方法的诸多不便，有研究提出了使用空气耦合超声导波同侧V透射法[1-3]。调整换能器间距和角度激励钢板中A₀模式导波，利用导波传播过程中产生的泄露波和水界面的一次反射波进行几何运算，计算出开闭器中水层厚度。

沿着大型棒状或板状结构长距离传播的超声波称为导波，在无损检测领域被广泛应用，导波的检测精度、检测范围都与导波的频率有关[4]。相对于传统的超声波检测技术，超声导波具有传播距离远、速度快的特点;因此，在大型构件（如在役管道）和复合材料板壳的无损检测中有良好的应用前景[5]。空气耦合超声波无损检测技术具有完全非接触、无损伤的特点，可用于传统超声检测手段难以适应的场合，空气耦合兰姆波可对复合材料的特性进行评价来达到真正意义的无损[6-9]。卢超等[10-11]利用空气耦合兰姆波同侧法对复合材料进行了成像检测，以无缺陷处信号值为基准，用信号差异系数作为特征值，对特征值全加和全乘的数据融合方法进行了缺陷形貌重构成像;本课题组分析了空气耦合超声穿透薄板时的能量透射率和各种板厚中的能量透射，使用空气耦合兰姆波同侧向和同侧异向法对钢板中开口损伤进行C扫描成像检测[12];张东波等[13]使用COMSOL有限元分析得到了板波的反射和透射声场，并观察到板波在结构中反射和投射的实际过程;张迪等[14]构建了流固耦合模型对空气声场及各向同性板材中的位移场进行了计算，得出相控阵声束动态偏转在板中能够激励出Lamb波的A₀和S₀模式这一结果。

本文使用有限积分法以开闭器为对象，模拟分析导波在开闭器中（空气—钢板—水界面）的传播过程，并依据这一传播过程利用几何声学计算方法计算水层厚度。最后将模拟结果与实验结果进行对比分析，验证其一致性。

1 超声导波检测原理及仿真计算

1.1 空耦超声穿透钢板时的能量透射率

超声波斜角入射时的反射和透射以及激发钢板中导波示意图如图1所示，当超声波从空气中以入射角θ、频率为f向钢板中入射时，在板中激发导波并在板中向前传播，且同时产生泄露波，该透射波的能量透射率计算公式[15]如下所示：其中θ为入射角;θ₁、θ_t分别为对应纵波和横波的折射角;ρ_a、ρ_s分别为空气和钢的密度;v_a、v₁、v_t分别空气中声速、钢板中纵波和横波速度，k_ly、k_ty是板厚方向的纵波和横波波数;Z、Z₁、Z_t分别为考虑了入射角的声阻抗;ω为角频率。

由式（1）可知超声波穿透钢板时的能量透射率不仅是两介质的密度和声速的函数，同时也是入射角和fd（频率与板厚的乘积）的函数，依据式（1）求得曲线关系图如图2，图3所示，分別为垂直入射和以θ=7.3°入射时能量透射率与频厚积关系图。由图3可知，当换能器为800kHz，钢板厚度为2.3mm，超声波以7.3°入射时，发生全透射，使泄露波能量到达最大，便于信号的采集和计算。

1.2 导波传播过程仿真及几何计算

本文使用有限积分法超声波传播模拟分析软件（SWAN21）对导波在开闭器中（空气—钢板—水）传播过程进行模拟分析，并对开闭器中水层厚度进行计算，建立如图4所示模型。模型结构为模拟开闭器结构，空间位置由上至下介质分别水、钢板、空气。模型数据为：水层厚度巧mm，钢板厚度2.3mm，空气禾禺合超声换能器频率800kHz、晶片直径14mm，激发导波模式为A₀模式，根据钢板厚度及频散曲线计算出最佳换能器角度θ=7.3°，在换能器左侧空气中设置超声波接收点，对接收波形进行A模式显示。

空气耦合超声波换能器发射超声波经过空气传导至钢板界面在钢板内反射并激发导波，导波在钢板中传播并向水介质以及空气中发生泄露，并且泄露的超声波在水中传播在水一真空界面会发生反射，反射的超声波会再次在钢板中激励导波并向水介质以及空气中发生泄露。下面，就这一传播过程以及超声波测量结果以时间顺序进行介绍。

图5为时间t=6.0μs处仿真图，此时换能器发出超声波并在钢板中激发导波，导波开始往水介质与空气中产生泄露波，但是由于此时空气中的泄露波距离换能器太近，在仿真过程中观察不到。往水中泄露的超声波角度为33.3°，声速为1.48km/s，导波沿着钢板向前传播，群速度为3.236km/s。

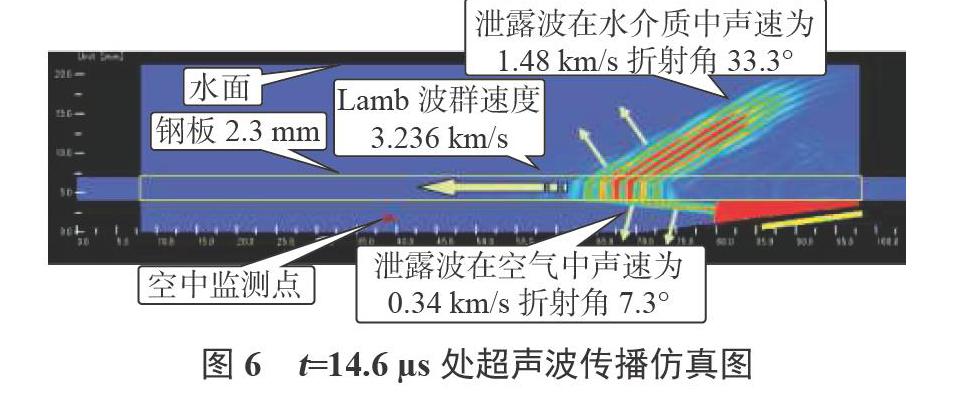
如图6所示，为时间t=14.6μs处仿真图，导波继续在钢板中传播，并且向水中和空气中发生泄露，导波往空气中泄露波与水平夹角为7.3°，往水中泄露波与水平夹角为33.3°，且垂直于各自波阵面传播，如图中箭头所示。

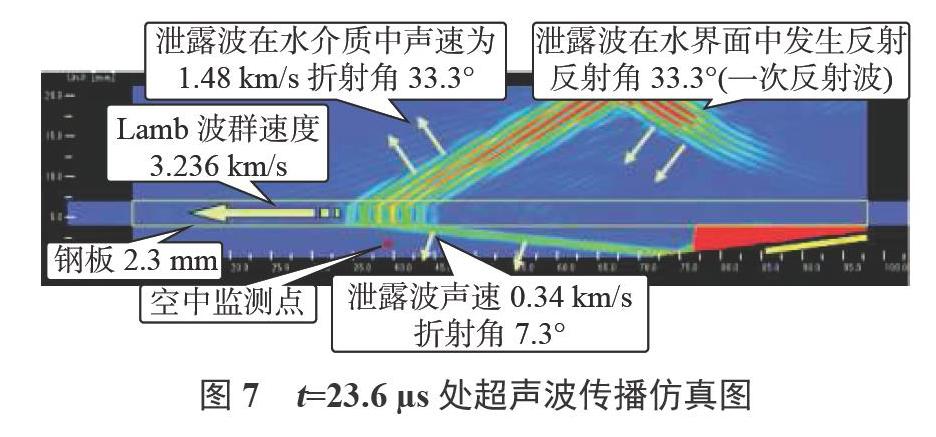
如图7所示，为时间t=23.6μs处仿真图，导播继续在钢板中传播，位于空中的监测点已经能够检测到泄露波。导波在水介质中的泄露往前传播遇到水，真空界面，立即发生一次反射，且反射角为33.3°，当一次反射波传播到钢板介质时，将会在钢板中再次激发导波，并沿钢板传播，且在传播过程继续往空气中和水介质中发生泄漏，角度与换能器激发导波产生泄露波角度相同。

图8为时间t=41.6μs处仿真图，水介质中泄露波在钢板中激发导波，并且在传播过程同时向水介质与空气中泄露，在水介质中产生的泄露波在水一真空界面发生反射，形成二次反射波。空气中最左侧，为换能器激发导波产生的泄露波，在监测点上方为水面一次反射波激发的导波产生的泄露波。

接收点接收到的波形如图9所示。A波形为空气耦合换能器激发钢板中导波的泄露波A显示，在t=28.4μs处，泄露波（沿空气—导波—空气路径）达到最大幅值;B波形为水界面的一次反射波在钢板中激励的导波往空气中泄露的波形A显示，在t=46.3μs处，泄露波（沿空气—导波—水介质—水面反射波（第一次）—导波—空气路径）达到最大幅值，即当水层厚度为15mm，波形A和B到达时间差为△t=17.9μs时，接收波形幅值最大。

基于以上模拟过程，改变水层厚度，可以求得水层厚度D与时间差△t的关系，简化计算模型如图10所示。超声波在B点处激励钢板中导波，并以r=33.3°传播至C点并产生一次反射波传播至E点，水面一次反射波在E点处激励钢板中导波，并往前传播△L距离，在G点被接收，AB与FG为超声波在空气中声程，B点至C点至E点为超声波水中传播声程，传播过程如图中箭头所示，B点至E点至F点为导波在钢板中声程。图中VW为超声波在水中传播速度、V_g为导波群速度、B为换能器倾斜角、r为折射角、D为水层深度、L₁为一次反射波出现距离，则时间差△t可由下列公式推导：

t_g1=L₁/V_g（2）

L₁=2Dtanr（3）

t_w1=2DV_w/ cosr（4）

式中：t_g1——導波在L₁段传播所用时间;

t_w1——超声波在水中传播时间。

对于图10有：

t_导波=t_a+t_g1+△t_g+t_b（5）

式中：t_导波——导波在整个传播过程中所用时间;

t_a、t_b——超声波在AB段及FG段传播时间;

△t_g——导波在△L段所用时间。

t_{一次反射波}=t_a+t_w1+△t_g+t_b（6）其中t_{一次反射波}为一次反射波传播总时间。

由上述分析可得时间差为：△t=t_w1-t_g1。

通过改变模型中水层厚度，当换能器频率为800kHz时，记录数据成表1，制成图11，可知水层厚度与时间差关系式为D=0.8258△t（η=0.8258），将水层厚度与时间差关系系数记为相关系数η。并且改变换能器频率，可得换能器频率与系数η曲线，如图12所示。

2 实验过程及结果

根据上文模拟过程，通过钢板中导波及一次反射回波的时间差△t能准确计算开闭器中水层厚度D，且制备了实验室状态下模拟开闭器装置，模型数据与仿真模型相同，如图13所示，在钢制容器内加水，由下至上依次为空气一钢板一水界面。检测装置由空气耦合专用换能器、高功率信号发射接收器（JPR600C）、高功率前置放大器（60dB）、处理软件模块组成。将开闭器固定于支架上，调整换能器角度为7.3°，空气耦合专用换能器频率为800kHz，移动接收换能器至65mm处，改变开闭器中水层厚度D分别为20，30，40，50mm，进行A显示，结果如图14所示。水层厚度D与时间At具有良好的线性关系，所求得系数η为0.8265;并且从A显示可以得出导波的传播时间不随水层厚度的变化而变化，而水面一次反射波传播时间随着水层厚度的增加而增加，因此在实际检测中，需要调整换能器之间距离对接收波形进行显示，使水面一次反射波更清晰、更准确。

接下来控制水层厚度为30mm，固定发射换能器，移动接收换能器，改变换能器之间距离，接收换能器以5mm的间隔往左移动，将换能器从相隔50mm移动至140mm处，在移动过程中同时对结果进行A显示和B显示，如图15所示。图15（a）为B显示结果，①为导波回波（沿空气—导波—空气路径），②为水面—次反射波回波（沿空气—导波—水—水面—次反射波—导波—空气路径），③为水面二次反射波回波（沿空气—导波—水—水面一次反射波—导波—水—水面二次反射波—导波—空气路径），④为水面三次反射波回波;图15（b）为A显示结果，由上至下分别为换能器之间距离65，95，125mm处波形。从图中能清楚地看到超声波包络数量、幅值和延时的变化。

对比仿真结果和实验结果具有高度一致性，验证了该方法的正确性和准确性，能够准确测量水层厚度。

3 结束语

1）本文通过模拟实验以及在实验室环境下使用超声导波法对开闭器中水层厚度进行了测量研究。实验结果与模拟实验结果具有高度的一致性，且利用导波与水面一次反射波时间差△t与水层厚度D的关系式来计算开闭器中水层厚度，方法简单，测量精度高、误差小。

2）在实际检测中，由于开闭器中水层厚度未知，但是能够通过装置设计上的优势根据实际情况改变换能器之间距离，使结果更准确。空气耦合超声导波法解决了接触式超声波法带来的诸多不便，为测量开闭器中水层厚度提供了新的思路、给空气耦合超声带来了更好的发展。

参考文献

[1]NAKAHATA K，CHANG J，TAKAHASHI M，et al.Finiteintegration technique for coupled acoustic and elastic wavesimulation and its application to noncontact ultrasonictesting[J].Acoustical Science and Technology，2014，35（5）：260-268.

[2]CHANG J，LU C，KAWASHIMA K.Development of Non-contact Air Coupled Ultrasonic Testing system for reinforcedconcrete structure[C]//Nondestructive Evaluation/Testing：New Technology&Application（FENDT），2013 Far EastForum on.IEEI{，2013：197-200.

[3]常俊杰，卢超，川嶋紘一郎.非接触空气耦合超声波的材料无损评价与检测[J].浙江理工大学学报，2015，33（7）：532-642.

[4]常俊杰，李媛媛，李光亚.钢轨轨头浅表面缺陷的空气耦合超声导波检测[J].无损检测，2018，40（3）：20-24.

[5]周正干，冯海伟.超声导波检测技术的研究进展[J].无损检测，2006，28（2）：57-63.

[6]CASTAINGS M，CAWLEY P.The generation，propagation，and detection of Lamb waves in plates using air-coupledultrasonic transducers[J].The Journal of the AcousticalSociety of America，1996，100（5）：3070-3077.

[7]常俊杰，盧超，小仓幸夫.非接触空气耦合超声检测原理及应用研究[J].无损探伤，2013，37（4）：6-11.

[8]周正干，魏东.空气耦合式超声波无损检测技术的发展[J].机械工程学报，2008，44（6）：10-14.

[9]CASTA]NGS M，HOSTEN B.Lamb and SH waves generatedand detected by air-coupled ultrasonic transducers incomposite material plates[J].Ndt&E International，2001，34（4）：249-258.

[10]饶璐雅.复合材料层板冲击损伤空气耦合兰姆波成像检测方法研究[D].南昌：南昌航空大学，2017.

[11]饶璐雅，陈果，卢超.碳纤维复合材料层板冲击损伤的空气幸禺合兰姆波成像检测[J].宇航材料工艺，2017，47（5）：69-74.

[12]常俊杰，魏强，卢超.非接触空气耦合超声波钢板探伤的应用研究[J].浙江理工大学学报，2015，33（11）：829-834.

[13]张东波，赵金峰，潘永东.空耦超声激发板波的COMSOL模拟[J].南京大学学报（自然科学），2015，51（S1）：129-133.

[14]张迪，昊先梅.基于有限元的空耦超声相控阵Lamb波激发与检测[J].应用声学，2015，34（3）：201-206.

[15]NISHINO H，MASUDA S，YOSHIDA K，et al.Theoreticaland experimental investigations of transmission coefficients oflongitudinal waves through metal plates immersed in air foruses of air coupled ultrasounds[J].Materials Transactions，2008，49（12）：2861-2867.

（编辑：莫婕）