U型截面薄壁件测量精度优化方法研究

摘要：为提高三坐标测量机在测量一种U型截面薄壁件时的测量精度，分别从温度和测量力两方面研究精度优化方法。基于物体热膨胀效应的原子热振动原理分析铝合金材料的热膨胀影响因素，将温度影响引入测量能力评估算法，得到可实施温度补偿的边界条件，利用Minitab对变温测量实验数据进行分析并拟合出该薄壁件在径向方向上的热膨胀函数，实现在温度边界范围内对测量结果进行精度优化;针对RDS XXT测头系统的内部构造，通过对测头结构进行力学分析并建立采点触发力学模型，确定该测头系统的采点触发模式为力矩触发，利用材料力学理论分析力矩触发模式下的被测件形变机理。测力及测量截面位置交叉测量实验结果表明：测杆长度越长，测力越小，且越靠近工件底部，测量误差越小，测量精度越高。

关键词：三坐标测量机;薄壁件;温度补偿;测量变形;测量精度

中图分类号：TB921 文献标志码：A 文章编号：1674-5124（2019）09-0021-06

收稿日期：2019-03-11;收到修改稿日期：2019-05-08

作者简介：王斌（1982-），男，天津市人，高级工程师，硕士，研究方向为精密测试技术。

0 引言

工業坐标测量机是国内外几何量测量领域普遍使用的精密测量设备，其测量精度的影响因素很多，包括静态因素和动态因素两大类[1-2]。静态因素主要包括温度、振动、量值溯源等;动态因素主要包括测量策略、测量力等。通过研究和分析国内外计量测试行业最新技术发展动态发现，为了有效减小测量误差，普遍采取制定国家或行业标准对坐标测量进行规范，如德国的VDA标准，严格规范了坐标机在使用环境、量值溯源等方面的技术要求，并强制贯标执行，使静态误差因素得到有效控制;欧洲的AUKOM坐标测量行业认证机构则通过实行技术资格认证制度，特别是对于形位公差的测量，建立了AUKOM GD&T专项认证标准，进而对坐标机的测量策略进行统一和规范，有效减少了动态因素所导致的误差[3-4]。

通过上述分析可以看出，三坐标测量机的测量多数误差来源可通过制定行业标准或加强操作的一致性加以消除，但是对于工件自身温度差异以及结构特点在测量时产生的测量误差，就需要结合材料的热膨胀系数和测力作用机理加以分析并优化，从而提高测量精度。国内外学者在这一领域进行了广泛研究。Valkov等[5]研究了航空铝合金板材的热膨胀系数，认为材料厚度对热膨胀变形有重要影响，并介绍了适于做热膨胀系数测定的制样方法，并采用光学法测量热膨胀系数。Kompan筀[6]分析了铝合金产品的不同设计结构与热膨胀系数的关系。上述研究主要解决铝合金材料热膨胀系数的测定精度、测定条件等问题[7]，缺乏对采用坐标测量机测量铝合金产品时工件温度与测量精度的关系分析，特别是对于薄壁件，其温度对测量精度的影响和补偿方法，尚未做相关深入研究。Laaouina等[8]研究了接触式测头采点触发时测力在工件表面的作用机理，以及工件由测力所导致的形变规律。Pan等[9]通过分析坐标机广泛采用的压电式触发测头的采点触发模式，建立力学模型，通过计算得到了测力对测量精度的影响关系式。上述研究虽然是针对压电式坐标机测头进行的分析研究，但对于本文研究具有重要的参考和借鉴意义[10]。

本文将对一种中心对称剖面呈U型的铝合金薄壁回转零件进行测量精度的温度补偿方法和测力影响消除方法研究。通过建立一种带入温度影响因素的测量能力评估算法，确定温度误差补偿的边界条件并拟合补偿算式;提出一种针对环形触发测头系统测力分析的力学模型，研究测力导致的形变机理，减小测力影响，提高测量精度。

1 工件温度对测量精度的影响分析及补偿方法

1.1 金属热膨胀模型分析及精度优化方法

热膨胀特性是物体的基本属性，由原子的热振动效应产生。根据原子理论模型可知，原子间势能u（r）与原子间的相互距离r存在一定的函数关系，因此，当原子间发生相互振动时，其间距由r₀变为r₀+x，而势能变为：

u（r）=u（r₀+x）（1）

由热力学统计原理及热膨胀系数概念，可得到物体的热膨胀系数α_CTE，T：

上式表征的是不同材料的热膨胀系数随着温度的不同而发生变化，由于铝合金的热膨胀系数受组分比例、金相组织、相间缺陷、相间差异性及加工工艺的热效应等因素影响[11]，其热效应很难用经典热膨胀系数计算方法得到。那么，在实际测量时，为研究铝合金的热膨胀特性，通常采用铝合金试件温度变化引起特定尺寸方向伸长量进行测试，绘制关系曲线，进而对不同温度时材料的热膨胀效应进行分析。

1.2 精度优化边界的温度条件

根据测量能力评估方法，测量设备的测量误差至少要小于被测参数设计公差的1/4，而被测工件的热形变所导致的偏差应与设备自身测量误差合并考虑，累计误差与被测参数设计因满足如下关系[12]：

（δ_热形变+δ_测量误差）热形变

1.3 温度补偿算式拟合

选取100件U型截面薄壁件，分别在17～23℃的温度范围内，测量各试件的直径、圆度、高度等设计参数，同时，测量过程中保持测量环境温度恒定。测量实验结果表明，温度影响主要体现在径向尺寸上。为此，以100个试件在不同温度条件下的测量平均值作为拟合元素，利用Minitab数据分析软件进行分析，生成温度系数函数模型如下：

φD=0.005229×T+C（7）其中，C为U型薄壁件的名义直径。温度系数函数模型可通过计算得到不同温度条件下的补偿值，可用于测量室在不具备恒温条件下的实时测量结果修正，保证了测量结果的准确性。

1.4 温度补偿结果验证实验

通过选取5个实验件，将其分别恒温至17～23℃范围内的各温度点，测量各温度点下的测量值并作为比对数据，利用比对数据与标准温度下（20℃）时的测量值（参考数据）进行对比，验证补偿效果，考核测量精度。实验结果如表1所示。

由表可知，5个测试件中补偿前测量误差最大达到0.021mm，而补偿后最大误差仅为0.005mm，测量精度有了提高了4倍多。通过温度补偿，在工件未完全恒温的狀态下，有效提高了坐标机的测量精度。

2 测力对精度的影响机理及优化方法

2.1 测头触发模式与测力的关系

三坐标测量机用测头可分为动态测头与静态测头两大类。Zeiss G2坐标机的RDS XXT测头系统是可实现动态（扫描式）和静态（触发式）测量的双模式信号采集系统，采用触发采点测量时，可以看作为静态测量，此时，测量力对工件造成的影响与测头系统的结构及触发模式有关。RDS XXT测头内部结构如图1（a）所示，1为测杆，2为环形保持架。测杆安装在环形保持架上，环形保持架的外壁布有均匀的触点，当测杆没有受到测量力时，环形保持架的外壁与触点均保持接触;当测杆的球状端部与工件接触时，至少会引起一个触点脱离接触，从而引起电路的断开，产生阶跃信号，完成测量触发采点[13]。

接触测量时，由于测头和工件存在相对运动，当被测表面有几何形状误差或对基准要素有位置误差，有可能使测头瞬时离开被测工件表面而产生测量误差。为了分析方便，将测针和测杆简化为等截面的测杆单元，质量为M，长度为L，作用于工件上的静测量力为F₀。当测针相对工件表面测量时，测杆单元绕支点做左右摆动，摆角为B，则测杆单元的力学方程为

由式（8）可以看出，测头系统的触发力学方程与测杆摆角关系较大，测头系统的结构决定了其摆动距离不大于图1中触点球径，而当θ较小时，该力学模型可简化为力矩方程，即测量力与测杆长度成反比。说明RDS XXT测头系统是由力矩触发采点的，可通过改变测杆长度控制测量力的大小。

如图1（b）所示，测头位于坐标系的Z轴的原点，测杆长度为尸，环形保持架半径OC的投影与X轴夹角φ₀，测头触碰零件产生的触发力为F（θ，φ），摆角θ和方位角φ直接影响触发力的方向。那么，如果当测头采点方向与零件柱面法线方向相同，极角θ和方位角φ不超过触点半径，则测力F可使测杆围绕A-B轴旋转，当环形保持架C离开触点时信号触发。因此，为保证采点触发而加载的测力将会使工件产生接触形变。此外，该测量力还会对测针造成弯曲，产生弯曲位移，进而导致工件弯曲变形。

2.2 测力所致形变对测量精度的影响

假设零件和测头不变，那么形变量只与测量力有关[14]，RDS XXT测头系统配置有3种不同的采点触发测量力模式，分别为敏感性触发、标准型触发和加力触发，分别对应不同的表面粗糙度状况的工件，敏感性触发模式主要用于测量表面光洁度较高的塑料、玻璃等工件的测量;标准型用于大多数金属材料的机加产品;加力触发用于表面粗糙的复合材料检测。因此，对于铝合金薄壁工件的检测，应采用标准型触发模式，其测力与测杆长度关系曲线如图2所示。

由图可以看出，随着测杆长度增加，3种测力模式的测力均呈减小趋势，当测杆长度为30mm时，3种测力模式的测力差值为0.05N，而当测杆长度为150mm时，测力差值为小于0.01N。

2.2.1 接触形变量计算

使用接触式量仪进行测量时，测头和被测工件的测量面直接接触，为了保证仪器与工件表面的可靠接触，需要一定大小的力作用于工件上，但测量力的存在也会使工件和测头产生接触变形。接触变形量的大小与工件的材料、测量力的大小有关[15]。

式中：F——测量力，N;

E——工件的弹性模量，GPa;

R₁——工件半径，mm;

R₂——测头半径，mm。

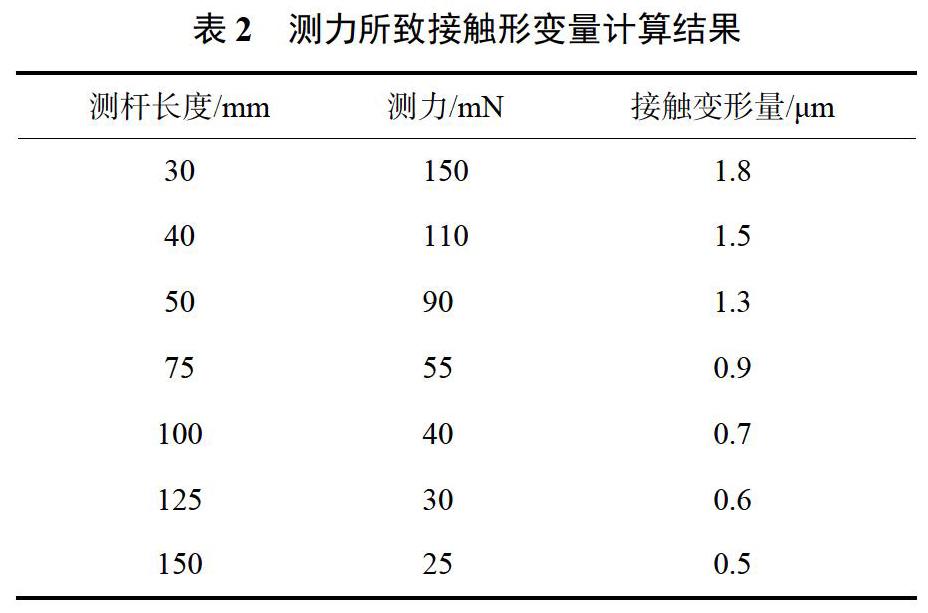
将铝合金材料弹性模量，测头球半径为1.5mm，代入公式（9），得到不同测力条件下的变形量如表2所示。

根据以上分析计算可以看出，当测杆长为30mm时，对应测量力为150mN，工件的接触变形量为1.8μm，同时由于测量过程中工件接触的均匀性，考虑到其接触变形量与被测参数公差比值较小以及测量机自身测量误差（1.9μm），其变形影响可忽略。

2.2.2 弯曲形变量计算

工件在测量力的作用下也会产生弯曲变形，弯曲变形量主要受测量位置以及测量力大小的影响。根据材料力学理论，工件在测量力的作用下产生的弯曲变形量[16]为

式中：F——测量力，N;

E——工件弹性模量，GPa;

I——工件截面惯性矩，N·m。

工件的弯曲变形不仅和工件的材料有关，其装夹位置的影响也较大。U型截面薄壁件的剖面尺寸结构如图3所示。

这样，可根据下式计算出U型截面薄壁件的惯性矩：

式中：B——工件外径，mm;

e₁——工件外底面至装卡截面距离，mm;

b——工件内径，mm;

h——工件内底面至装卡截面距离，mm;

a/2——工件壁厚，mm;

e₂——工件端面至装卡截面距离，mm。

弯曲变形量与装卡位置的关系，用工件装夹高度H与工件直径的比值i作为装夹位置，考虑到该薄壁件的轴向长度，装卡位置差△H设置2mm。选取测力为55mN，测杆长度为75mm，将各参数代入公式（10），计算出不同测量截面测量力与弯曲变形量的关系如表3所示。

由表可以看出，随着测量力的增加，其弯曲变形量也在增加，并且随着测量位置的升高，其弯曲变形量最大达到了6.2μm，可见弯曲变形的影响是造成测量误差的主要原因[17]。所以，在测量速度、测量长度一定的条件下，测量采点位置越靠近工件底部，误差越小，精度越高。

2.3 测力及测量位置与精度关系验证实验

2.3.1 测力与精度关系验证实验

选取5个U型薄壁件，编号记为1^#～5^#，在同一测量截面高度（△H=2mm）以不同的测量力连续测量10次，记录并计算10次测量结果的极差值，考核其测量精度，测量实验结果如表4所示。

由表测量结果可以看出，随着测量力的不断增加，测量误差越来越大，精度逐渐下降。可见，测量力导致的弯曲形变对精度的影响较为显著，与理论计算结果一致。

2.3.2 测量位置与精度关系验证实验

仍选取2.3.1选用的5个试验件，以相同的测量力（40mN）在不同的截面高度连续测量10次，记录并计算10次测量结果的极差值，考核其测量精度，测量实验结果如表5所示。

由表可以看出，随着测量截面高度的不断增加，测量误差越来越大，精度逐渐下降。可见，测量位置距离定位位置越远，测力导致的弯曲形变效应越显著，同样与理论计算结果一致。

3 结束语

本文针对U型截面薄壁件在加工过程中会由热效应或环境温度热传导而产生变形的特点，通过变温实验建立了尺寸温度补偿算式，保证测量结果的准确性;通过分析三坐标测量机RDS XXT测头系统的结构及采点触发原理，确定了该测头系统的静态测量力所导致工件形变主要为弯曲变形，对于U型截面薄壁易变形件，测量精度实验结果表明，通过合理配置测杆长度及采点高度，可有效提高此工件的测量精度。

参考文献

[1]张国雄.三坐标测量机[M].天津：天津大学出版社，1999.

[2]罗哉.关节臂式坐标测量机测量力误差分析及补偿[J].仪器仪表学报，2017（5）：1159-1166.

[3]YOUNES E，ABDERRAZAK E O，AHMED C.Experimentalinvestigation of dynamic errors in coordinate measuringmachines for high speed measurement[J].InternationalJournal of Precision Engineering and Manufacturing，2018，19（8）：1115-1124.

[4]HUSSAIN M，（！U J，ENGEL R，et al.Designed experiment tofind the optimal combination of the factors for the coordinatemeasuring machine（CMM）to measure cylindricity of enginecylinder bore[C]//International Conference on IndustrialEngineering&Operations Management，2015.

[5]VALKOV S，NEOV D，BEZDUSHNYI R，et al.Study of themicrostructure，crystallographic structure and thermal stabilityof Al-Ti-Nb alloys produced by selective electron beamalloying[J].Journal of Surface Investigation：X-ray，Synchrotron and Neutron Techniques，2018，12（3）：436-441.

[6]KOMPAN T A，KONDRATIEV S V，KORENEV A S，et al.Measurement of the thermal expansion coefficient for ultra-high temperatures up to 3000 K[J].International Journal ofThermophysics，2018，39（3）：40.

[7]程湘红.三坐标测量机测量误差分析及处理[J].工程技术研究，2018（1）：113-114，160.

[8]LAAOUINA L，NAFI A，MOUCHTACHI A，et al.Application of CMM separation method for identifyingabsolute values of probe errors and machine errors[C]//International Conference on Engineering&Mis，2016.

[9]PAN F，NIE L，BAI Y，et al.Geometric errors measurementfor coordinate measuring machines[J].IOP Conference SeriesEarth and Environmental Science，2017，81（1）：012117.

[10]KALUS J，JORGENSEN J K.Measuring deformation andmechanical properties of weld lines in short fibre reinforcedthermoplastics using digital image correlation[J].PolymerTesting，2014，36：44-53.

[11]丁鴻章.工程金属材料热膨胀系数的计算[J].浙江工业大学学报，2000，28（4）：358-366.

[12]黄晓明，孙杰，李剑锋，等.7050-T7451铝合金预拉伸板材热膨胀系数变化规律及机理[J].中国有色金属学报，2013（12）：3282-3288.

[13]刘育楠，董学军，刘红刚，等.三坐标测量机测头系统精度验证方法研究[J].工业计量，2016，26（6）：41-45.

[14]邵竑文，孟亮，刘斯宇.论测量力对几何尺寸测量结果的影响[J].计量与测试技术，2015，42（12）：52-54.

[15]李志渤，黄强先，赵剑，等.接触测量中的微探球力变形研究[J].中国机械工程，2014（14）：1126-1129.

[16]熊伟，葛志华，唐威，等.轮毅轴承接触应力及变形量计算与分析[J].机械工程师，2018（10）：119-121.

[17]邱江月，夏金利.探讨测量力对测试结果的影响[J].工业计量，2010（2）：365-366.

（编辑：商丹丹）