特征指标信息融合的电动调节阀故障诊断

王印松 王珏

摘要：调节阀作为控制系统的重要组成部分，它的故障诊断对于指导控制过程安全稳定地运行至关重要。为提高故障诊断的精确率，解决电动调节阀不同故障间可能存在相互关联的问题，提出一种基于特征指标信息融合的诊断方法。利用电动调节阀可测变量间的关系，计算能够反映电动调节阀不同故障特点的指标，并建立与之对应的神经网络;然后将每个神经网络的输出看作独立的证据体进行D-S证据融合，得到最终的诊断结果。实验结果及现场分析表明：该方法充分利用数据的有效信息，从不同侧面对故障进行诊断，能够有效地应用于电动调节阀的故障诊断，具有较高的应用价值。

关键词：故障诊断;电动调节阀;D-S证据理论;神经网络;特征指标

中图分类号：TP273 文献标志码：A 文章编号：1674-5124（2019）09-0006-07

收稿日期：2019-03-25;收到修改稿日期：2019-04-18

基金项目：国家自然基金联合基金项目（U1709211）

作者简介：王印松（1967-），男，河北河间市人，教授，博士，研究方向为先进控制策略和控制系统故障诊断技术。

0 引言

近年来，随着新型工业化进程的复杂化和智能化，工业控制系统往往具有非线性和不确定性的特点。调节阀作为整个控制系统的执行终端部件，对控制系统品质的优劣具有很大的影响;但由于使用环境较为恶劣，调节阀容易出现多种故障[1]。据统计，调节阀的故障占到控制系统总故障的三分之一以上，更重要的是，由于闭环控制系统的反馈作用，调节阀的故障表现不明显，它的故障往往被掩盖。因此对调节阀故障诊断技术进行研究，提高故障诊断的准确率，对于保障控制过程安全稳定地运行具有重要意义。

调节阀作为工业过程控制系统的重要部件，目前已有较多国内外学者对调节阀的故障诊断开展了研究。现有的诊断方法主要分为基于解析模型、数据驱动和专家知识3类[2]，针对调节阀的故障诊断，Goncalves等[3]对调节阀开度、扭矩等相关信号进行小波包变换后，利用能量谱密度信息和自组织映射实现了对调节阀故障的检测与诊断。Garcia等[4]提出了一种调节阀的集成故障诊断方法，将矩形拟合法、曲线拟合法、直方图法和双相关分析法进行集成，并根据可靠性指标选取其中最优的方法完成对调节阀故障的诊断。Hafaifa等[5]推导了调节阀位移信号对压差信号的传递函数，并利用神经网络对其时间常数及放大系数进行建模，对调节阀的故障进行分离，但为获得精确的诊断结果，该方法往往需要大量的训练样本，而实际生产过程中，要获取大量各种类型的故障样本十分困难。郭胜辉等[6]提出了基于区间观测器的方法，该方法需要考虑过程的数学模型，然而在实际中，过程模型往往难以获取，这使得这种方法在实际应用上遇到巨大障碍。针对过程模型难以获取这一问题，黄孝彬等[7]提出了一种基于执行机构部件信号分析的故障诊断方法，通过分析输入信号和输出信号的变化趋势进行故障诊断，该方法不需要考虑过程模型且易于实现;但控制回路中的干扰因素，会对信号的变化趋势产生影响，从而影响诊断效果。

结合上述问题，为提高调节阀故障诊断的准确率，本文以电动调节阀为例，提出了一种基于特征指标D-S证据融合的故障诊断方法。该方法提出了能够反映调节阀信号趋势的特征指标及计算方法，并将神经网络与D-S证据理论进行结合，对不同指标反映的故障信息进行融合，得到最终的诊断结果。通过搭建双容水箱系统模拟电动调节阀不同故障，验证了该方法的有效性;并将该方法应用到火电机组主汽温系统减温水调节阀中，验证了该方法的实用性。

1 电动调节阀工作原理及常见故障类型

1.1 电动调节阀工作原理

电动调节阀由电动执行机构和阀门两部分构成，电动调节阀工作原理方框图如图1所示。

在电动调节阀中，输入信号与位置发送器传送的阀杆位移反馈信号进行比较后形成偏差信号，经伺服放大器放大后以驱动伺服电机的有效转动，再经减速器减速，触发阀杆动作以调节阀门开度[8]。

1.2 电动调节阀常见故障分析

调节阀的故障可以分为执行机构故障和阀体故障2类，通过对电动调节阀的常见故障进行分析，可以归为偏差故障、增益故障、卡死故障、死区故障和粘滞故障这5类，它们各自的故障表现如表1所示。

2 调节阀各项特征指标的计算

在实际的生产过程中，调节阀的指令信号OP和阀位反馈信号MV都是可以直接测得的，因此本文采用的各项指标均可以通过这两个信号计算得到。

1）电动调节阀基本偏差

基本偏差（Bias）指一段采样时间内，阀位反馈信号与指令信号差值绝对值的平均：

其中n为采样点个数。

2）电动调节阀基本增益

基本增益（Gain）指一段采样时间内，阀位反馈信号与指令信号变化量比值的平均：

3）电动调节阀稳定度函数

稳定度函数（Steady）指调节阀指令信号稳定度因子与阀位反馈信号稳定度因子差值的绝对值。其中，稳定度因子（SF）是一种可以衡量某一信号波动状态的函数[9]，计算公式如下：其中，SF_op、SF_mv分别为调节阀指令信号稳定度因子、阀位反馈信号稳定度因子;y_max、y_min、y_mean分别为一段时间内过程数据的最大值、最小值和平均值。

4）电动调节阀死区大小

死区大小（Dead）指调节阀输入指令信号正反方向变化不引起阀门位置有任何可察覺变化的有限区间，计算公式如下：

Dead=|op_s+d-op_s|其中，s为调节阀指令信号开始发生变化的采样时刻，d为指令信号变化不引起阀门位置变化的区间长度。

5）电动调节阀粘滞指标

调节阀动作过程中，由于阀杆静摩擦等因素的存在，调节阀往往存在粘滞特性，当控制器输出量的增量不足以克服摩擦力时，调节阀的位置保持不变。调节阀的粘滞特性如图2所示，可以用4个阶段来表示：AB-死区阶段;BC-粘滞阶段;CD-滑动跳跃阶段：DE-连续运动阶段[10]。

结合调节阀粘滞特性曲线图，本文采用调节阀动态输入-输出特性的形状检测方法用于粘滞指标（Yama）的计算[11]。具体计算步骤如下：

a）对指令信号OP和阀位反馈信号MV分别求差分△OP、△MV，并对差分序列进行定性化处理，分为S（steady）、I（increase）、D（decrease）3种状态。

b）建立OP-MV变化情况的模型，如IS表示此时OP信号状态为I、MV信号状态为S;ISII表示此时OP信号状态为L，MV信号状态为S，且下一时刻OP信号状态为I、MV信号状态为I。

c）计算各状态的模型数目τ。

d）计算粘滞指标，即除其他因素引起的IS和DS状态在所有关系里（SS状态除外）所占的比例：其中，τ_total为总时间。

6）控制系统性能评价指标

工业过程中控制回路的故障会降低控制系统性能，为监测工业过程运行状况及不同故障对控制系统性能的影响，需要对控制系统性能进行准确的评价。采用最常用的基于最小方差控制的性能评价指标（minimum variance control，MVC）[12]，对电动调节阀在不同工作状况下系统的性能进行评价。该方法不会对系统产生影响，评价过程大致为：首先估计过程的时延，并利用输出数据辨识出从扰动输入端到系统输出端的传递函数模型;然后根据时延信息分离出反馈控制不变项，计算系统的最小方差基准值σ_MV²及系统输出的实际方差σ_y²，得到基于最小方差的性能指标MVC：

MVC=σ_MV²/σ_y²（6）

最小方差的性能指标MVC的取值范围为[0，1]，越接近0则说明性能越差;越接近1则说明性能越好。

3 基于D-S理论的信息融合

3.1 D-S证据理论基本概念

D-S（Dempster-Shafer）证据理论又称信任理论，它使用可信度来对各命题发生的可能性进行度量。D-S证据理论具有较强的理论基础，能够处理随机性以及模糊性所导致的不确定性，因此在信息融合方面得到了广泛的应用[13]。

3.1.1 基本概率分配函数

将D-S证据理论的识别框架记为，其中包括有限个基本命题，记为{A₁，A₂，…，A_n}。若存在集函数m：2[0，1]满足：其中，φ为空集。则称m（A）为识别框架的基本概率分配函数（mass函数），它表示了对命题A的信任程度。

3.1.2 信任函数

在识别框架上，对于任意一个假设命题A的信任函数（BEL）可以定义为

信任函数又可称为下限函数，它代表了对命题A的全部信任程度，即命题A的信任函数表示了直接证据对命题的支持程度。

3.1.3 似然函数（P1）

在識别框架上，对于任意一个假设命题A的似然函数（PL）可以定义为

似然函数又可称为上限函数，它代表了不否定命题A的信任程度，即命题A的似然函数表示了潜在证据对命题的支持程度。

3.2 D-S证据理论合成规则

Dempster提出了一种合成规则，设m₁，m₂分别为同一识别框架上的两个基本概率分配函数，相应的焦元分别为A₁，A₂，…，A_k和B₁，B₂，…，B_r，且设其中，K为包含完全冲突假设A_i和B_j的所有基本概率分配函数乘积之和，当K=0时，表示m₁和m₂相互矛盾，两个函数之间不能进行合成，当K≠0时，合成后的基本概率分配函数m：2→[0，1]可表示为其中，A指假设A_i和B_j组合的一个新的综合命题，A的基本概率分配函数m（A）是包含不冲突假设A_i和B_j的所有基本概率分配函数乘积之和。

3.3 神经网络与D-S证据理论的结合

D-S证据理论中基本概率分配函数的确定，是利用D-S证据理论进行信息融合的前提，也是最为关键的一步[14]。而在故障诊断中，基本概率分配函数通常根据专家经验来确定，主观性较强，不同的专家由同一个证据对同一个命题会给出不同的信度分配，有时差别很大。因此，为实现不同证据体基本概率分配函数赋值的客观化，避免构造基本概率分配函数的复杂性，本文将每个独立的神经网络作为一个证据体，将神经网络的输出值进行转换得到各命题的基本概率分配函数，具体计算公式[15]为其中，f_j表示故障模式;m_i（f_j）命题fj基于第i个神经网络诊断结果的基本概率分配函数;M_i（f_j）表示第i个神经网络第J个神经元的输出值;e_k表示神经网络的样本误差;m_i（θ）表示诊断结果不确定的可能性。

4 基于信息融合的电动调节阀故障诊断

4.1 电动调节阀故障诊断过程

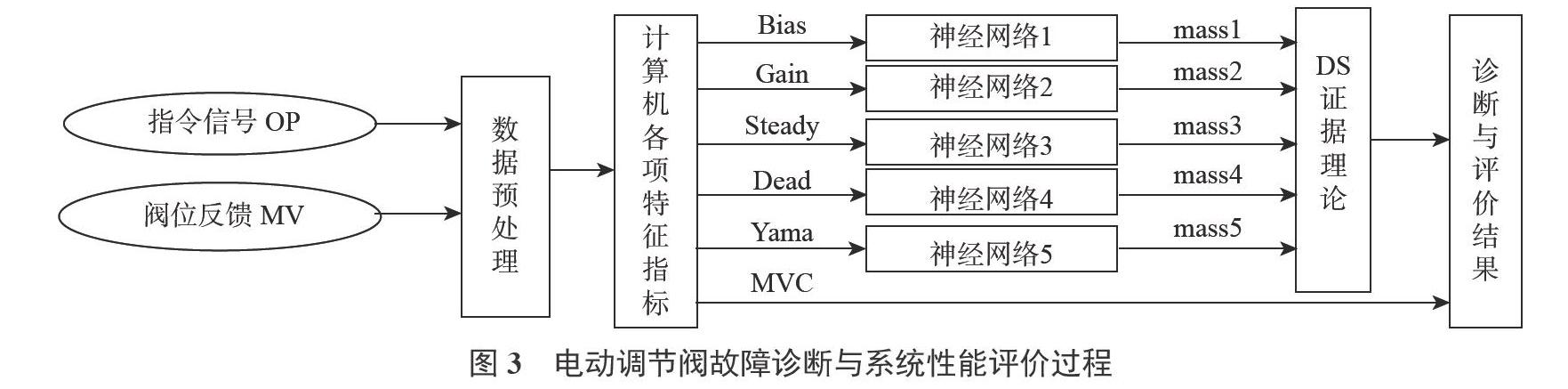
电动调节阀故障诊断与系统性能评价的过程如图3所示。首先根据调节阀指令信号和阀门位置反馈信号，计算调节阀的基本误差、基本增益、稳定度函数、死区大小、粘滞指标后，分别构建5个不同的神经网络;然后将每个神经网络看作独立的证据体，并根据神经网络的输出计算D-S证据理论的基本概率分配函数;最后根据D-S证据理论合成规则进行信息融合得到最终的诊断结果，并根据控制系统性能评价指标（MVC）的大小对控制系统进行评价。

4.2 仿真实验与结果分析

为验证本文提出方法的有效性，利用基于Ovation的A3030过程控制综合实验平台搭建双容水箱串级控制系统，该平台能实现温度、压力、流量、液位定值等控制系统，并使用Ovation DCS系统进行控制。该过程实验装置如图4所示。

人为模拟电动调节阀正常状态F₀、偏差F₁、增益F₂、卡死F₃、死区F₄及粘滞F₅不同工作状态，共同构成识别框架■={F₀，F₁，F₂，F₃，F₄，F₅}。记录10min内，电动调节阀指令信号与阀位反馈信号各600组数据，其中400组作为训练数据，剩余200组作为测试数据。

对训练数据和测试数据进行数据预处理后，计算各项指标，以其中一组训练数据为例，不同工作情况下的各项指标值如表2所示。

从表中可以看出，当不同故障产生时，部分特征指标会对应发生明显变化。比较不同故障下系统性能评价指标（MVC）的大小可知，调节阀的不同故障对系统性能有着不同的影响;其中电动调节阀在卡死和粘滞故障下，MVC仅为0.063 5和0.1012，因此，调节阀的卡死和粘滞对控制系统影响较为严重。接下来，将计算得到的指标值分别作为神经网络的输入进行训练以生成D-S证据理论的基本概率分配函数。本文利用Matlab构造BP神经网络，每个BP神经网络模型训练次数为10000次，训练目标为0.0001，学习速率为0.01。由于篇幅原因，仅展示死区故障下各神经网络的输出结果和经过D-S证据理论融合后的诊断结果，分别如表3和表4所示。

由表3和表4可见，经过D-S融合后，解决了诊断结果的不确定性，诊断结果更加精确。为验证本文所提出方法的优越性，进行如下实验：

实验1：直接根据电动调节阀指令信号、位置反馈信号，采用神经网络对故障分类，并将神经网络的输出值转换为基本概率分配值，完成诊断。

实验2：计算本文所提电动调节阀各项特征指标后，通过神经网络训练后，将神经网络的输出值转换为基本概率分配值，不进行信息融合，完成诊断。

实验3：即本文提出的方法。

其中，上述3个实验用到的实验数据及神经网络参数设置均相同。并设置诊断结果决策规则：最终定位的故障类型与其他故障的基本概率分配值之差必须大于某一阈值，本文经大量调试并结合实际诊断情况后将阈值确定为0.4。根据以上诊断规则确定实验1、实验2及实验3的诊断结果分别如表5-表7所示。

分析表5可知，直接根据电动调节阀输入输出数据进行诊断时，故障诊断准确率较低，且无法区分偏差故障和死区故障;分析表6可知，利用能够反映调节阀故障特点的特征指标进行故障诊断，可以提高诊断的准确率，但由于不同的故障可能导致相同的故障现象，因此诊断结果还存在不确定性;分析表7可知，经过D-S证据理论融合后，可以将不同故障准确地诊断出来。将上述3种方法在不同故障下的诊断结果进行比较，如图5所示。

整理上述3种方法的诊断准确率，实验1和实验2的诊断准确率分别为69.31和76.29%，本文所提方法的诊断准确率为98.23%。因此本文提出的方法，大大提高了电动调节阀故障诊断的准确性，解决了诊断结果的不确定性，减少了误判的可能。

4.3 诊断实例

本文将上述故障诊断方法应用到某电厂主汽温系统减温水电动调节阀中，采集2018年7月28日20：00-2018年7月29日6：00这10h内的数据，其中，电动调节阀指令信号OP和调节阀位置反馈信号MV变化曲线如图6所示。

计算该系统性能评价指标后，发现在22：08到22：48这段时间内系统性能降低，按照本文提出的方法，计算得到这段时间内调节阀各项特征指标，如表8所示，且D-S信息融合后得到的诊断结果如表9所示。分析表8和表9可知，這段时间内，减温水电动调节阀发生了偏差故障，诊断结果与现场的实际情况相符。此时控制系统评价指标为0.6512，说明此时控制系统性能有待提高，需要解决调节阀偏差故障问题，提高系统性能。

5 结束语

本文提出了一种基于特征指标信息融合的故障诊断方法，并应用到电动调节阀中。实验结果表明，利用能够反映调节阀部件信号趋势变化的各项指标进行调节阀的故障诊断，有助于提高故障识别率，降低算法的复杂度，并且能够准确判断不同程度的故障对控制系统性能的影响;利用D-S证据理论进行信息融合，能够有效地解决故障定位不确定的问题;并且将神经网络的输出值进行转换后作为D-S证据理论的的基本概率分配函数，实现了基本概率分配函数赋值的客观化。因此，基于特征指标信急融合的方法对电动调节阀故障诊断具有工程意义。

参考文献

[1]YANG J，ZHU F，WANG X，et al.Robust sliding-modeobserver-based sensor fault estimation，actuator fault detectionand isolation for uncertain nonlinear systems[J].InternationalJournal of Control，Automation and Systems，2015，13（5）：1037-1046.

[2]周东华，刘洋，何潇.闭环系统故障诊断技术综述[J].自动化学报，2013，39（11）：1933-1943.

[3]GONCALVES L F，BOSA J L，BALEN T R，et al.Faultdetection，diagnosis and prediction in electrical valves usingself-organizing maps[J].Journal of Electronic Testing，2011，27（4）：551-564.

[4]GARCIA O P，TIKKALA V M，ZAKHAROV A，et al.Integrated FDD system for valve stiction in a paperboardmachine[J].Control Engineering Practice，2013，21（6）：818-828.

[5]HAFAIFA A，DJEDDI A Z，DAOUDI A.Fault detection andisolation in industrial control valve based on artificial neuralnetworks diagnosis[J].Control engineering and appliedInformatics，2013，15（3）：61-69.

[6]郭胜辉，朱芳来.基于区间观测器的执行器故障检测[J].控制与决策，2016，31（6）：1118-1122.

[7]黄孝彬.火电厂控制系统故障检测与诊断的研究[D].保定：华北电力大学，2004.

[8]黄爱芹.基于数据驱动的调节阀故障诊断方法研究[D].济南：山东大学，2015.

[9]刘吉臻，高萌，吕游，等.过程运行数据的稳态检测方法综述[J].仪器仪表学报，2013，34（8）：61-70.

[10]李士哲，王印松，田靖雨，等.气动阀门粘滞模型仿真及控制系统振荡分析[J].计算机仿真，2016，33（1）：239-244.

[11]YAMASHITA Y.An automatic method for detection of valvestiction in process control loops[J].Control EngineeringPractice，2006，14（5）：503-510.

[12]王印松，田靖雨，李士哲，等.基于时域指标的火电机组负荷控制系统性能模糊綜合评价[J].热力发电，2016，45（10）：99-103.

[13]KHAMSEH S A，SEDIGH A K，MOSHIRI B，et al.Controlperformance assessment based on sensor fusion techniques[J].Control Engineering Practice，2016，49：14-28.

[14]韩德强，杨艺，韩崇昭.DS证据理论研究进展及相关问题探讨[J].控制与决策，2014，29（1）：1-11.

[15]张文元，赵卫国，晋涛，等.多神经网络与证据理论的变压器故障诊断方法[J].高压电器，2018，54（8）：207-211.

（编辑：商丹丹）