水力学水头损失实验数学模型研究

张宏伟 解斯达 王彩霞 黄丽丽 刘静茹

(大连海洋大学海洋与土木工程学院，辽宁 大连 116000)

0 引言

水力学是理工科院校水利、土木、环境等专业的一门专业基础课程，水力学实验是其中一个非常重要的教学与实践环节[1]，而计算水力学作为一门独立的新型学科，形成于20世纪60年代中期，它论述如何用计算方法来研究水力学问题。而目前国内高校所开设的实验课程，基本上为教学模具的演示、验证实验。作为信息时代的现在，显然这种教学手段已经不足以承载培育创造、创业、创新的“三创”人才的需求。因此，将计算水力学引入到传统的水力学实验中，通过构建数学模型，利用数学解析方式获得实验参数，是迫在眉睫的改革和创新。因此，本文针对水力学实验中的局部水头损失实验做了如下探讨性研究。

1 局部水头损失模型实验原理

水流在运动过程中，受到边界条件或者过水断面的影响，造成水体各质点的流速、压强也随之发生改变，流动遭受破坏，产生涡流，各水质点之间运动加强，形成摩擦阻力，造成能量损耗，由此产生局部水头损失。

2 局部水头损失数学模型的构建

计算流体力学以质量守恒定律、动量守恒定律和能量守恒定律为基础，将已知流体运动基本规律进行数学公式描述，如欧拉方程、N-S方程等等，并将得到的数学方程离散，在初始条件、边界条件下通过计算机求解这些控制流体流动的数学方程[2]。是目前应用最广泛的一门学科。此外，随着数值计算方法的迅速发展和计算机技术的不断进步，针对复杂水力学问题进行高精度、高分辨率的数值求解与可视化已经成为可能[3]。因此，计算水力学不仅是一门研究水流运动规律的学科，同时也可以说是一门研究如何利用计算机进行实验的课程。该课程的学习在为学生后续课程学习打下良好的理论基础的同时，也为学生今后进行工程实践和科研工作提供了重要的学习工具。

2.1 控制方程

A1V1=A2V2=Q——连续方程；

∑F=ρQ(β2V2-β1V1)——动量方程。

2.2 网格划分

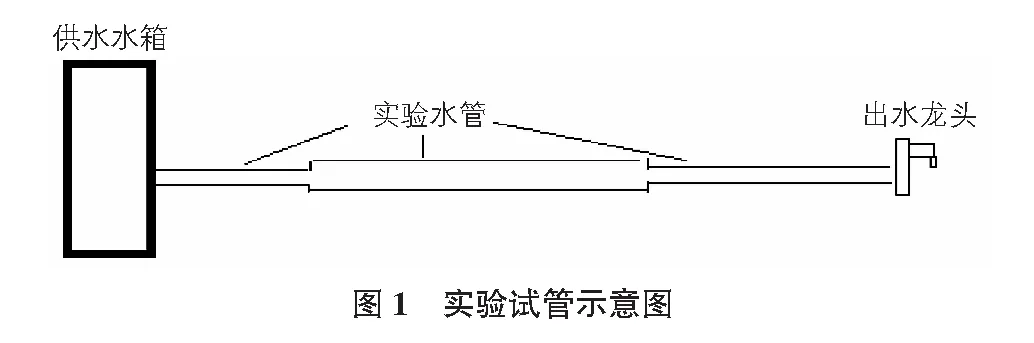
为了更科学合理地解析实验水管内流体运动形态如图1所示，充分考虑到流体在实验水管内因管径摩擦力以及管径的突变影响，现将实验试管单元划分，降低因为试管长度而造成的实验误差。

本数学模型所采用网格间距Δx=5 cm，将实验试管进行剖分(如图2所示)，并按图3程序控制流程，调动程序进行数值计算模拟。

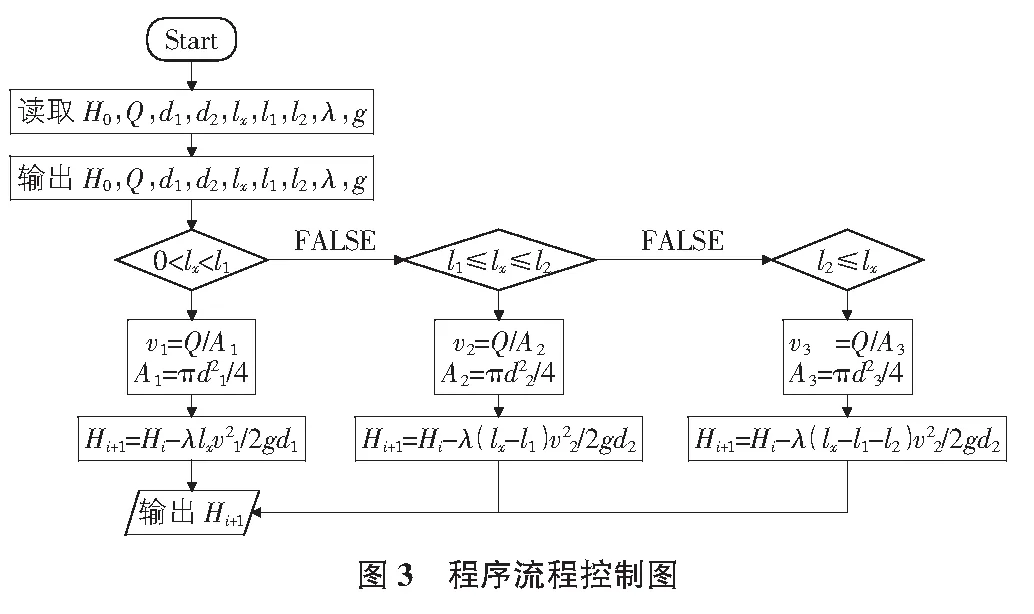
2.3 离散方程及程序控制流程

利用FORTRAN语言进行结构化程序设计的核心在于将实际问题分成数据和过程两部分考虑, 将水力学三大基本方程即连续性方程、能量方程、动量方程离散化[4]，通过对静态子模块的数据进行存储、分析、处理，并且通过动态的程序执行过程来最后得到结果。整个程序模块化,这样每个静态子模块保证只有一个出入口,分别编译,单独执行,易于保证源程序的正确性、易读性以及易检查错误[5]。

AiVi=Ai+1Vi+1=Qi——连续方程；

∑Fi=ρQ(βi+1Vi+1-βiVi)——动量方程。

2.4 实验结果比析

分别通过水龙头控制，将水量调整到最大Q=106.53 cm3/s和最小状态Q=88.58 cm3/s。通过本数学模型进行数值计算，结果如图4，图5所示。

通过图4和图5实际结果和数值计算结果对比，数据吻合较好。可以通过数值计算过程更好地理解出控制方程各个参数的实际意义。也为现在的水力学实验模式提供了另一种可能。

3 结语

实验的数学模型是对传统实验教学手段的有益补充，通过对控制方程各个参数的理解，可以加深学生对流体运动内在实质的理解，从而能够激发学生对流体力学这门课程的兴趣，激发其创新力。

本文所采用的汇编语言为FORTRAN语言，系统为开源系统。在实验过程中，学生可以进行自主编译，加入其他实验参数，对程序精准度不断进行修正完善。从以前的单纯的验证实验，到利用数学模型解析实验参数，再到自主性创新性实验，可以最大程度调动学生的学习主动性、能动性和学习热情。为智能信息时代培育储备人才。

目前，本文所构建的局部水头损失数学模型仅仅处于起步阶段，下一步要对流体力学实验中其他水力现象作进一步的研究。逐渐形成一整套数学模型实验平台。