北京地区深基坑桩锚支护结构协同变形分析研究

单宝学 倪晓荣 李哲琳

(中国新兴建设开发有限责任公司，北京 100039)

1 概述

北京地处华北平原内陆，地貌单元属冲洪积扇，地层岩性由以卵石类土、砂类土为主渐变为以粉土、粘性土为主的交互地层，土质较硬，力学性质较好，故深基坑水平拉力支护结构一般采用锚杆或锚索。基坑开挖后，边坡外侧压力永久性削弱，使得土体中原有应力平衡体系被打破，水平向主应力减小，在土体自重的作用下，竖向应力因侧向阻力减小而产生额外压力，造成边坡下沉，从而使得土体向侧向挤压，形成位移。如果侧压力减小至一定程度，位移持续增大，将产生边坡滑移，最后导致塌方。

在有支挡结构的边坡侧向变形过程中，支挡结构起了抗力的作用，它给边坡重新提供了侧压力，使得边坡重新保持了静力平衡，边坡位移无法继续发展。同时，因为受到支挡结构的影响，在提供相同侧压力的情况下，不同的支挡结构，边坡的位移是不同的，因为土体在变形的过程中，其和支挡结构发生了协同变形，即一部分变形转移给了支挡结构。

支挡结构受到土压力作用后，自身产生了挠曲，理论上该挠曲没有结构力学中计算的纯受侧压力的挠曲大，因为在挠曲变形过程中，同时挤压土体，使得土体产生了抗力，又抵制了支挡结构继续自由变形。

当最后位移稳定下来之后，支挡结构的挠曲位移将和土体侧向位移一致，也就是支挡结构和土体的协同变形。

2 现行规程计算理论

现行规程计算理论主要为增量法，即在单个阶段，当墙体刚度不发生变化时，支护结构增量荷载产生的内力与前一个施工阶段完成后已产生的位移和内力叠加，再求得当前施工阶段完成后体系的实际位移和内力。每一步增量位移内力计算则采用全量法求解当前增量步下的位移。其求解位移内力的计算方法为弹性支点法，计算简图如图1所示。

支护结构的基本挠曲方程应按以下公式确定：

0≤z≤hn时：

z≥hn时：

3 现行规程计算理论的不足

现行规程计算边坡位移都是将支护结构水平变形作为边坡位移，计算时根据挠曲方程利用杆系有限元方法求解得到支护结构水平变形，而没有考虑支护结构与土体协同变形情况。故为求得更加符合现场实际情况的边坡位移，需要对协同变形进行考虑，目前行业内一般采用连续介质有限元法。

连续介质有限元法是将土体、围护结构以及土体与围护结构的接触面进行单元划分，比如面层单元、桩单元、锚杆单元、土体单元等，每个单元可定义不同的变形模型，比如土体单元一般采用弹塑性本构模型，围护桩、锚杆考虑为线弹性单元。三维连续介质有限元法计算较杆系有限元法更复杂，需采用ADINA或ABAQUS等大型有限元计算软件进行计算，不适合进行施工推广，故还需对传统增量法进行改进。

4 现行规程计算理论的改进

支护结构受到土压力作用后，产生向坑内弯曲形变，考虑到土体和支护桩紧密结合，故形变过程中支护结构将会带动土体一起形变，在支护桩产生弯曲变形的过程中，其后背土体将对桩产生抗力，使桩不能自由变形，最后实际位移也将小于理论值。

那么如何对现行公式进行改进，可以从以下几方面着手：

1)土体对支护桩变形起反作用，可以考虑适当提高支护桩刚度，因为桩身和土体共同变形，支护结构的刚度应在支护桩刚度的基础上适当增加土体刚度，刚度增加值可根据土层性质确定，粉土和粘土层取低值，砂卵石层取高值，具体可根据当地工程经验确定。

2)围护桩变形后，土体也跟着变形，在变形过程中，土压力随着位移的发展将呈现衰减，该减小值与位移有关系，位移越大，衰减越大，这是因为土体经过压密后，φ值将增加，为达到新的极限平衡状态，σ3将减小。

5 刚度改进

桩身刚度为EI，E为换算混凝土弹性模量，I为换算截面惯性矩，截面惯性矩与截面模量相关，截面模量又称为截面的抵抗矩。在协同作用下，土体刚度将和桩身刚度叠加，在计算时可用叠加后的刚度代替桩身刚度。土体刚度计算时假设影响桩后协同影响厚度及宽度按1D考虑，简图如图2所示。

土体刚度计算如下，参考桩身刚度计算公式：

EI=0.85EdI0=0.85EdD4/12。

其中，EI为土体抗弯刚度；Ed为土体弹性模量；I0为土体截面惯性矩；Ed按照中硬粘土考虑，取8 MPa。桩径为0.8 m时，土体刚度为2.3×1011N·mm2，相当于护坡桩刚度同比增加，桩身混凝土强度按照C25考虑，弹性模量为28 000 MPa，则惯性矩增加8.28×106mm4，大致相当于桩径增加114 mm。

6 土压力改进

现行规程开挖面以上土压力按照主动土压力考虑，边坡开挖后，侧压力急剧降低，桩身瞬间承压，在分步开挖下，假设桩体已趋于稳定，土压力也趋于稳定，下步工况开挖后，位移继续增大，位移增大的过程类似于侧向土压力减小，根据胡克定律，侧压力减小量与位移有如下关系：

根据上述公式，即可根据边坡位移情况求解土压力减小量，根据土压力变化值即可求得新压力状态下的围护结构内力。假设基坑槽深中点深度按照10 m考虑，中点位移为10 mm，φ值为30°时，则单位宽度土压力减少值为13.8 kPa。土压力的减小相当于土体抗力的增加，每层土体单独进行计算，换算公式如下：

其中，z为支护结构顶部至计算土层底部深度;hn为地面至计算土层顶部深度；h为1/2地面至计算土层顶部深度，即hn/2；E为地面至计算土层顶部加权平均重度；φ为地面至计算土层顶部加权平均内摩擦角；y为计算土层位移，假设为s/20。

求得m如下：

其中，z-hn为土层计算厚度。

7 案例应用

拟建工程位于北京市朝阳区金台西路，基坑深度为17.1 m。场区周边环境复杂，北侧、南侧、东侧均紧邻已有建筑，西侧紧邻金台西路。拟建场区工程地质、水文地质条件简述如下：

根据岩土工程勘察报告，拟建场区地层岩性及其分布特征自上而下主要描述如下：

房渣土、碎石填土①层，粉质粘土～粘质粉土②层，粉质粘土～重粉质粘土③层，卵石～圆砾④层，粉质粘土～粘质粉土⑤层，卵石⑥层。

基础开挖范围内分布有一层地下水，稳定水位埋深为14.30～15.30，含水层主要为砂卵石层，地下水类型为层间潜水。

地层分布情况见表1。

表1 地层分布情况表

7.1 位移内力规程计算结果

拟建工程典型基坑边坡模型示意见图3。

基坑周边堆载条件见图4，表2。

表2 周边堆载条件表

根据软件计算，位移及弯矩计算结果见图5。

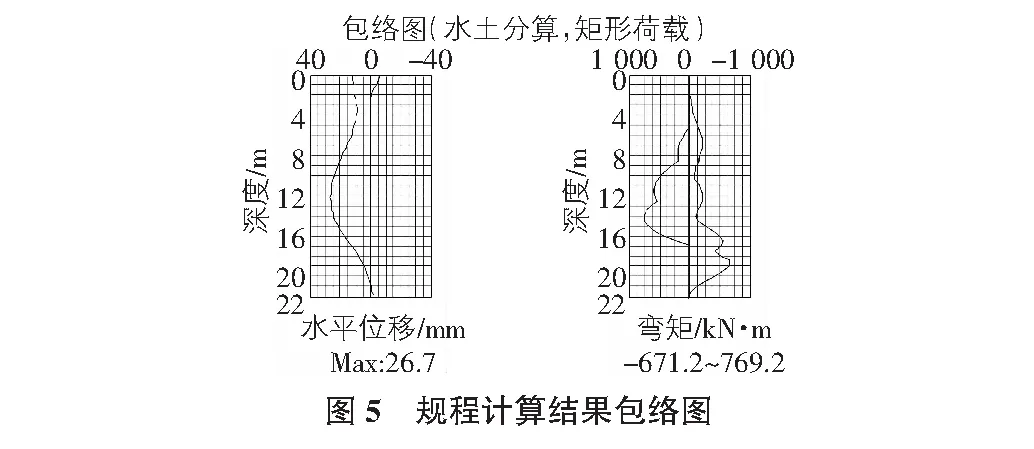
计算得坡顶最大位移为12.5 mm。桩体最大位移为26.7 mm。

7.2 位移内力改进计算结果

周边堆载等各项条件与规程相同，桩体直径按照刚度叠加调整为0.91 m，m值增加计算结果见表3。

表3 m值增加计算明细表

将增加的m值与按规程计算得到的m值进行叠加，重新计算后位移及弯矩计算结果见图6。

计算得坡顶最大位移为11.5 mm。桩体最大位移为21.5 mm。

7.3 位移内力与现场对照结果

现场实际坡顶位移监测数据见图7。

根据现场实际监测结果，坡顶最大位移为10.0 mm，改进后计算结果与实际比较接近。

8 结语

本文通过刚度叠加和土体抗力换算对桩锚支护结构深基坑协同变形进行了简化分析，理论分析结果与实际监测数据较为接近，对北京地区相关类似分析具有指导意义和参考价值。但因为现场情况千变万化，各种因素作用错综复杂，尤其是初始m值的确定仍具有较强的经验性，想准确计算出协同变形仍比较困难，本文通过简化计算方法对此进行了探讨，具有一定的创新性和实用性。